Некоторые свойства элементарных функций
1. Идемпотентность & и Ú: х&x=x , xÚx=x.
2. Коммутативность &,Ú,Å,|,~, 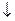 .
.
3. Ассоциативность &,Ú,Å,~, поэтому в формулах вида xyz можно не ставить никаких скобок.
4. Дистрибутивность:
а) & по отношению к Ú: x&(yÚz)=xyÚxz ,
б) Ú по отношению к &: xÚ(y&z)=(xÚy)&(xÚz) ,
в) & по отношению к Å: x(yÅz)=xyÅxz .
5. Инволюция : 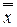 =х .
=х .
6. Правило де Моргана: 
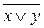 =
= 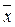 &
& 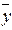 и
и 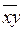 =
= 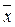 Ú
Ú 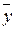 .
.
7. Законы действия с 0 и 1:
xÚ0=x , xÚ1=1 , xÚ 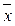 =1 , x&0=0 , x&1=x , x&
=1 , x&0=0 , x&1=x , x& 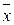 =0 , xÅ1=
=0 , xÅ1= 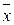 , xÅ0=x.
, xÅ0=x.
8. Самодистрибутивность импликации: x  (y
(y  z)=(x
z)=(x  y)
y)  (x
(x  z).
z).
Равенство всех этих формул доказывается по определению, т.е. по равенству функций, которые они реализуют.
Проверим для примера самодистрибутивность импликации : x  (y
(y  z)=(x
z)=(x  y)
y)  (x
(x  z).
z).
| x | y | z | y  z z
| x  (y (y  z) z)
| x  y y
| x  z z
| 
|
Следствия из свойств элементарных функций
1. Законы склеивания:
xyÚx  =x(yÚ
=x(yÚ 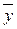 )=x
)=x 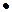 1=x (дистрибутивность & относительно Ú);
1=x (дистрибутивность & относительно Ú);
(xÚy)&(x 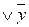 )=x
)=x 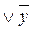 y =xÚ 0=x (дистрибутивность Ú относительно &).
y =xÚ 0=x (дистрибутивность Ú относительно &).
2. Законы поглощения:
xÚxy=x(1Úy)=x 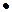 1=x; x&(xÚy)=xÚxy=x.
1=x; x&(xÚy)=xÚxy=x.
Свойства элементарных функций и теорема о замене подформул на эквивалентные позволяют упрощать формулы.
Пример 3:
Упростим формулы:
1. x2x3Úx1 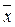 2x3 = x3(x2Úx1
2x3 = x3(x2Úx1 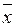 2) = x3((x2Úx1)&(x2Ú
2) = x3((x2Úx1)&(x2Ú 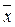 2)) = (x1Úx2)x3.
2)) = (x1Úx2)x3.
2. x1Ú 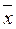 1x2Ú
1x2Ú 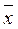 1
1 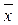 2x3Ú
2x3Ú 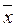 1
1 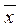 2x3x4 = x1Ú
2x3x4 = x1Ú 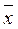 1(x2Ú
1(x2Ú 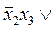
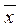 2
2 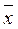 3x4) = x1Ú
3x4) = x1Ú 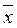 1(x2Úx3Ú
1(x2Úx3Ú 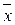 2
2 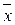 3x4) = (x1Ú
3x4) = (x1Ú 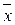 1)(x1Úx2Úx3Ú
1)(x1Úx2Úx3Ú 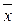 2
2 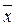 3х4) = x1Ú(x2Úx3)Ú(
3х4) = x1Ú(x2Úx3)Ú( 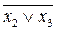 )x4 = x1Ú(x2Úх3Ú(
)x4 = x1Ú(x2Úх3Ú( 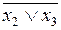 ))(x2Úx3Úx4) = x1Úx2Úx3Úx4.
))(x2Úx3Úx4) = x1Úx2Úx3Úx4.
Дата добавления: 2016-03-27; просмотров: 754;
