Задачи по комбинаторике
1.Расписание одного дня содержит 5 уроков. Определить количество таких расписаний при выборе из одиннадцати дисциплин.
Ответ: 55 440.
2.Комиссия состоит из председателя, его заместителя и еще пяти человек. Сколькими способами члены комиссии могут распределять между собой обязанности?
Ответ: 42.
3.Сколькими способами можно выбрать трех дежурных из группы в 20 человек?
Ответ: 1 140.
4.Сколько различных звукосочетаний можно взять на десяти выбранных клавишах рояля, если каждое звукосочетание может содержать от трех до десяти звуков?
Ответ: 968.
5.В вазе стоят 10 красных и 5 розовых гвоздик. Сколькими способами можно выбрать из вазы пять гвоздик одного цвета?
Ответ: 253.
6.Номера трамвайных маршрутов иногда обозначаются двумя цветными фонарями. Какое количество различных маршрутов можно обозначить, если использовать фонари восьми цветов?
Ответ: 64.
7.Чемпионат, в котором участвуют 16 команд, проводится в два круга (т.е. каждая команда дважды встречается с любой другой). Определить, какое количество встреч следует провести.
Ответ: 240.
8.Замок открывается только в том случае, если набран определенный трехзначный номер. Попытка состоит в том, что набирают наугад три цифры из заданных пяти цифр. Угадать номер удалось только на последней из всех возможных попыток. Сколько попыток предшествовало удачной?
Ответ: 124.
9.Из группы в 15 человек выбирают четырех участников эстафеты 800+400+200+100. Сколькими способами можно расставить спортсменов по этапам эстафеты?
Ответ: 32 760.
10.Команда из пяти человек выступает на соревнованиях по плаванию, в которых участвуют еще 20 спортсменов. Сколькими способами могут распределиться места, занятые членами этой команды?
Ответ: 25!/20!.
11.Сколькими способами можно расположить на шахматной доске две ладьи так, чтобы одна не могла взять другую? (Одна ладья может взять другую, если она находиться с ней на одной горизонтали или на одной вертикали шахматной доски.)
Ответ: 3 126.
12.Две ладьи различного цвета расположены на шахматной доске так, что каждая может взять другую. Сколько существует таких расположений?
Ответ: 896.
13.Порядок выступления восьми участников конкурса определяется жребием. Сколько различных исходов жеребьевки при этом возможно?
Ответ: 8!.
14.Тридцать человек разбиты на три группы по десять человек в каждой. Сколько может быть различных составов групп?
Ответ: 30!/(10!) 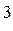 .
.
15.Сколько четырехзначных чисел, делящихся на 5, можно составить из цифр 0, 1, 3, 5, 7, если каждое число не должно содержать одинаковых цифр?
Ответ: 42.
16.Сколько различных светящихся колец можно сделать, расположив по окружности 10 разноцветных лампочек (кольца считаются одинаковыми при одинаковом порядке следования цветов)?
Ответ: 9!.
17.На книжной полке помещается 30 томов. Сколькими способами их можно расставить, чтобы при этом первый и второй тома не стояли рядом?
Ответ: 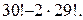
18.Четыре стрелка должны поразить восемь мишеней (каждый по две). Сколькими способами они могут распределить мишени между собой?
Ответ: 2 520.
19.Из группы в 12 человек ежедневно в течение 6 дней выбирают двух дежурных. Определить количество различных списков дежурных, если каждый человек дежурит один раз.
Ответ: 12!/(2!) 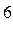 .
.
20.Сколько четырехзначных чисел, составленных из цифр 0, 1, 2, 3, 4, 5, содержат цифру 3 (цифры в числах не повторяются )?
Ответ: 204.
21.Десять групп занимаются в десяти расположенных подряд аудиториях. Сколько существует вариантов расписания, при которых группы №1 и №2 находились бы в соседних аудиториях?
Ответ: 2×9!.
22.В турнире участвуют 16 шахматистов. Определить количество различных расписаний первого тура (расписания считаются различными, если отличаются участниками хотя бы одной партии; цвет фигур и номер доски не учитываются).
Ответ : 2 027 025.
23.Шесть ящиков различных материалов доставляются на пять этажей стройки. Сколькими способами можно распределить материалы по этажам? В скольких вариантах на пятый этаж доставлен какой-либо один материал?
Ответ: 56; 6×45.
24.Два почтальона должны разнести 10 писем по 10 адресам. Сколькими способами они могут распределить работу?
Ответ: 210.
25.Поезд метро делает 16 остановок, на которых выходят все пассажиры. Сколькими способами могут распределиться между этими остановками 100 пассажиров, вошедших в поезд на конечной остановке?
Ответ: 16100.
26.Сколько трехзначных чисел, делящихся на 3, можно составить из цифр 0, 1, 2, 3, 4, 5, если каждое число не должно содержать одинаковых цифр?
Ответ: 40.
27.Собрание из 80 человек избирает председателя, секретаря и трех членов ревизионной комиссии. Сколькими способами это можно сделать?
Ответ: 80!(3! ×75!).
28.Из 10 теннисисток и 6 теннисистов составляют 4 смешанные пары. Сколькими способами это можно сделать?
Ответ: 10!/48.
29.Три автомашины №1,2,3 должны доставить товар в шесть магазинов. Сколькими способами можно использовать машины, если грузоподъемность каждой из них позволяет взять товар сразу для всех магазинов и если две машины в один и тот же магазин не направляются? Сколько вариантов маршрута возможно, если решено использовать только машину №1?
Ответ: 36×6!.
30.Четверо юношей и две девушки выбирают спортивную секцию. В секцию хоккея и бокса принимают только юношей, в секцию художественной гимнастики – только девушек, а в лыжную и конькобежную секции – и юношей, и девушек. Сколькими способами могут распределиться между секциями эти шесть человек?
Ответ: 2304.
31.Из лаборатории, в которой работает 20 человек, 5 сотрудников должны уехать в командировку. Сколько может быть различных составов этой группы, если начальник лаборатории, его заместитель и главный инженер одновременно уезжать не должны?
Ответ: 15 368.
32.В фортепьянном кружке занимаются 10 человек, в кружке художественного слова –15, в вокальном кружке – 12, в фотокружке – 20 человек. Сколькими способами можно составить бригаду из четырех чтецов, трех пианистов, пяти певцов и одного фотографа?
Ответ: 15!10/7!
33.Двадцать восемь костей домино распределены между четырьмя игроками. Сколько возможно различных распределений?
Ответ: 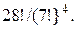
34.Из группы в 15 человек должны быть выделены бригадир и 4 члена бригады. Сколькими способами это можно сделать?
Ответ: 15 015.
35.Пять учеников следует распределить по трем параллельным классам. Сколькими способами это можно сделать?
Ответ: 35.
36.Лифт останавливается на 10 этажах. Сколькими способами могут распределиться между этими остановками 8 пассажиров, находящихся в лифте?
Ответ: 108.
37.Восемь авторов должны написать книгу из шестнадцати глав. Сколькими способами возможно распределение материала между авторами, если два человека напишут по три главы, четыре – по две, два – по одной главе книги?
Ответ: 16!/(26×32).
38.В шахматном турнире участвуют 8 шахматистов третьего разряда, 6 – второго и 2 перворазрядника. Определить количество таких составов первого тура, чтобы шахматисты одной категории встречались между собой (цвет фигур не учитывается).
Ответ: 420.
39.Из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 составляются всевозможные пятизначные числа: не содержащие одинаковых цифр. Определить количество чисел, в которых есть цифры 2, 4 и 5 одновременно.
Ответ: 1800.
40.Семь яблок и два апельсина надо положить в два пакета так, чтобы в каждом пакете был хотя бы один апельсин и чтобы количество фруктов в них было одинаковым. Сколькими способами это можно сделать?
Ответ: 105.
41.Буквы азбуки Морзе состоят из символов (точек и тире). Сколько букв можно изобразить, если потребовать, чтобы каждая буква содержала не более пяти символов?
Ответ: 62.
42.Номер автомобильного прицепа состоит из двух букв и четырех цифр. Сколько различных номеров можно составить, используя 30 букв и 10 цифр?
Ответ: 9×106.
43.Садовник должен в течение трех дней посадить 10 деревьев. Сколькими способами он может распределить по дням работу, если будет сажать не менее одного дерева в день?
Ответ: 36.
44.Из вазы, где стоят 10 красных и 4 розовых гвоздики, выбирают один красный и два розовых цветка. Сколькими способами это можно сделать?
Ответ: 60.
45.Двенадцати ученикам выданы два варианта контрольной работы. Сколькими способами можно посадить учеников в два ряда, чтобы у сидящих рядом не было одинаковых вариантов, а у сидящих друг за другом был один и тот же вариант?
Ответ: 2(6!)2.
46.Каждый из десяти радистов пункта А старается установить связь с каждым из двадцати радистов пункта Б. Сколько возможно различных вариантов такой связи?
Ответ: 2200.
47.Шесть ящиков различных материалов доставляют на восемь этажей стройки. Сколькими способами можно распределить материалы по этажам? В скольких вариантах на восьмой этаж будет доставлено не более двух материалов?
Ответ: 86; 86–13×75.
48.Сколькими способами можно построить в одну шеренгу игроков двух футбольных команд так, чтобы при этом два футболиста одной команды не стояли рядом?
Ответ: 2(11!)2.
49.На книжной полке книги по математике и по логике – всего 20 книг. Показать, что наибольшее количество вариантов комплекта, содержащего 5 книг по математике и 5 книг по логике, возможно в том случае, когда число книг на полке по каждому предмету равно 10.
Ответ: C510–x × C510+x 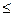 (C510)2 .
(C510)2 .
50.Лифт, в котором находятся 9 пассажиров, может останавливаться на десяти этажах. Пассажиры группами выходят по два, три и четыре человека. Сколькими способами это может произойти?
Ответ: 10!/4.
51.«Ранним утром на рыбалку улыбающийся Игорь мчался босиком». Сколько различных осмысленных предложений можно составить, используя часть слов этого предложения, но не изменяя порядка их следования?
Ответ: 23.
52.В шахматной встрече двух команд по 8 человек участники партий и цвет фигур каждого участника определяются жеребьевкой. Каково число различных исходов жеребьевки?
Ответ: 
53.A и B и еще 8 человек стоят в очереди. Сколькими способами можно расположить людей в очереди, чтобы A и B были отделены друг от друга тремя лицами?
Ответ: 6 × 8! × 2!.
54.Сколько четырехзначных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, если а) цифры не повторяются; б) цифры могут повторяться; в) используются только нечетные цифры и могут повторяться; г) должны получиться только нечетные числа и цифры могут повторяться.
Ответ: а) 5 × 5 × 4 × 3=300; б) 5 × 6 = 1080; в) 34; г) 5 × 6 × 6 × 3 = 540.
55.В классе изучается 10 предметов. Сколькими способами можно составить расписание на понедельник, если в понедельник должно быть 6 уроков и все разные?
Ответ: 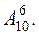
56.На одной прямой взято m точек, на параллельной ей прямой n точек. Сколько треугольников с вершинами в этих точках можно получить?
Ответ: 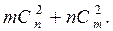
57. Сколько есть пятизначных чисел, которые читаются одинаково справа налево и слева направо, например, 67876.
Ответ: 9 × 10 × 10 = 900.
58.Сколько разных делителей (включая 1 и само число) имеет число
35 × 54?
Ответ: 30.
59.В прямоугольной матрице A = {aij} m строк и n столбцов. Каждое aijÎ{+1, –1}, причем произведение aij по любой строке или любому столбцу равно 1. Сколько таких матриц?
Ответ: 2(m–1)(n–1).
60.В комнате n лампочек. Сколько разных способов освещения комнаты,
при которых горит:
а) ровно k лампочек (k < n);
б) хотя бы одна лампочка.
Ответ: а) 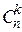 ; б)
; б) 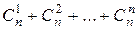 = 2n–1.
= 2n–1.
61.Сколько имеется четырехзначных чисел, у которых каждая следующая цифра больше предыдущей?
Ответ: 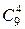 = 126.
= 126.
62.Сколько имеется четырехзначных чисел, у которых каждая следующая цифра меньше предыдущей?
Ответ: 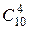 = 210.
= 210.
63.Имеется p белых и q черных шаров. Сколькими способами их можно выложить в ряд, чтобы никакие 2 черных шара не лежали рядом (q £ p + 1)?
Ответ: 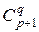 .
.
64.Имеется p разных книг в красных переплетах и q разных книг в синих переплетах (q £ p + 1). Сколькими способами их можно расставить в ряд, чтобы никакие две книги в синих переплетах не стояли рядом?
Ответ: 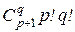 .
.
65.Сколькими способами можно упорядочить {1, 2, ... n} чисел так, чтобы числа 1, 2, 3 стояли рядом в порядке возрастания?
Ответ: (n – 2)!.
66. На собрании должны выступить 4 докладчика: A, B, C и D, причем B не может выступить раньше A. Сколькими способами можно установить их очередность.
Ответ: 12 = 3! + 2× 2 +2.
67. Сколькими способами m + n + s предметов можно распределить на 3 группы, чтобы в одной группе было m предметов, в другой – n, в третьей – s предметов.
Ответ: 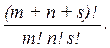
68. Сколько целых неотрицательных решений имеет уравнение x1+ x2+ ... + xm= n.
Ответ: 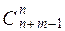 .
.
69.Найти число векторов Z = (a1a2... an), координаты которых удовлетворяют условиям:
1) aiÎ {0, 1};
2) aiÎ {0, 1, ... k – 1};
3) aiÎ {0, 1, ... ki– 1};
4) aiÎ {0, 1} и a1+ a2+ ... + an= r.
Ответ: 1) 2n; 2) kn; 3) k1k2... kn; 4) 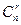 .
.
70.Каково число матриц {aij}, где aijÎ{0,1} и в которой m строк и n столбцов? 1) строки могут повторяться; 2) строки попарно различны.
Ответ: 1) 2m×n; 2) 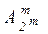 .
.
71.Дано m предметов одного сорта и n другого. Найти число выборок, составленных из r элементов одного сорта и s другого.
Ответ: 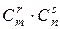 .
.
72.Сколькими способами число n можно представить в виде суммы k натуральных слагаемых (представления, различающиеся лишь порядком слагаемых считаются разными).
Ответ: 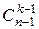 .
.
73.Бросаются 10 одинаковых игральных костей. Сколькими способами они могут упасть так, что :
1) ни на одной кости не выпадет 6 очков;
2) хотя бы на одной кости выпадет 6 очков;
3) ровно на 3-х костях выпадет 6 очков;
4) ровно на 3-х костях выпадет 6 очков, на 2-х других выпадет 5 очков.
Ответ : 510, 610-510, 24´58, 630´46
74.Считая, что телефонные номера состоят из 7 цифр, причем могут начинаться и с 0 тоже, найти число телефонных номеров, таких что:
1) 4 последние цифры одинаковы и не встречаются среди первых 3-х (первые 3 цифры различны.);
2) все цифры различны ;
3) номер начинается с цифры 5;
4) номер содержит три цифры 5, две цифры 1 и две цифры 2.
Ответ : 5040, 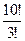 , 106, 210.
, 106, 210.
75.10 человек, среди которых Иванов и Петров, размещаются в гостинице в двух 3-х местных и в одном 4-х местном номерах. Сколькими способами они могут быть размещены ? Сколькими способами их можно разместить, если Иванов и Петров помещены в 4-х местный номер ?
Ответ: 4200, 560.
76. 52 карты раздаются 4-м игрокам, каждому по 13 карт. Сколькими способами их можно раздать, если
1) каждый игрок получит туза;
2) один из игроков получит все 13 карт единой масти ;
3) все тузы попадут к одному из игроков;
4) 2 определенных игрока не получат ни одного туза.
Ответ: 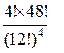 ,
, 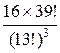 ,
, 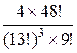 ,
, 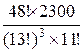 .
.
77. Регистр калькулятора содержит 8 разрядов. Сколько будет 8-ми значных чисел, если
1) регистр содержит ровно 2 одинаковые цифры ;
2) регистр содержит ровно 2 пары одинаковых цифр;
3) регистр содержит ровно 3 одинаковые цифры;
4) регистр содержит не более 3-х различных цифр.
Ответ: 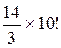 ,
, 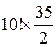 ,
, 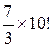 ,
,  .
.
78. Сколькими способами можно выстроить 9 человек:
1) в колонну по одному;
2) в колонну по 3, если в каждой шеренге люди выстраиваются по росту и нет людей одинакового роста?
Ответ: 9!, 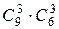 .
.
79. Из n букв, среди которых a встречается α раз, буква b встречается β раз, а остальные буквы попарно различны, составляются слова. Сколько среди них будет различных r-буквенных слов, содержащих h раз букву a и k раз букву b?
Ответ: 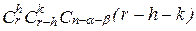 .
.
80. Имеется колода из 4n (n³5) карт, которая содержит карты 4-х мастей по n карт каждой масти, занумерованных числами 1,2…n. Подсчитать, сколькими способами можно выбрать 5 карт так, что среди них окажутся:
1) 5 последовательных карт одной масти;
2) 4 карты из 5-ти с одинаковыми номерами;
3) 3 карты с одним номером и 2 карты с другим;
4) 5 карт одной масти;
5) 5 последовательно занумерованных карт;
6) 3 карты из 5-ти с одним и тем же номером;
7) не более 2-х карт каждой масти.
Ответ: 4(n–4), 4n(n–1), 12n(n–1), 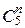 , 45(n–4),
, 45(n–4), 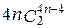 ,
, 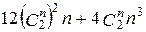 .
.
81. Сколькими способами можно расставить n нулей и k единиц так, чтобы между любыми 2-мя единицами находилось не менее m нулей?
Ответ: 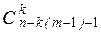 .
.
Дата добавления: 2016-03-27; просмотров: 4747;
