Принцип двойственности
Определение 1. Функции f*(x1, ..., xn) называется двойственной к функции f(x1, ..., xn), если f*(x1, ..., xn) = 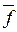 (
( 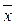 1, ...,
1, ..., 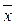 n).
n).
Пример 1. Покажем с помощью таблицы истинности, что константа 0 двойственна к 1:
| x | f | f* |
Функции f(x) = x и g(x) = 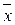 двойственны сами себе:
двойственны сами себе:
| x | f | f* | g | g* |
так как f*(0)= 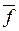 (1).
(1).
Определение 2. Если f*(x1, ..., xn) = f(x1, ..., xn), то f(x1, ..., xn) называется самодвойственной.
Пример 2.Покажем, что f(x1,x2,x3)=x1Åx2Åx3 – самодвойственна:
| x1 | x2 | x3 | f | f* |
Если f*– самодвойственна, то 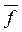 (
( 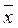 1, ...,
1, ..., 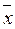 n) = f(x1, ..., xn), т.е. на противоположных наборах функция принимает противоположные значения.
n) = f(x1, ..., xn), т.е. на противоположных наборах функция принимает противоположные значения.
Пример 3. Покажем, что функция х1Úх2 двойственна к x1&x2, функция х1 х2 двойственна к функции x1|x2.
| x1 x2 | f=х1Úх2 | f* | g=x1|x2 | g*=x1 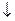 x2 x2
|
| 0 0 0 1 1 0 1 1 |
Теорема о двойственных функциях
Если f* двойственна к f, то f двойственна к f*.
Доказательство. f*(x1, ..., xn) = 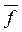 (
( 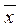 1, ...,
1, ..., 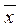 n). Найдем двойственную функцию к f*, т.е. (f*( x1, ..., xn))* = (
n). Найдем двойственную функцию к f*, т.е. (f*( x1, ..., xn))* = ( 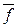 (
( 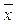 1, ...,
1, ..., 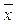 n))* =
n))* =  (
( 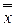 1, ...,
1, ..., 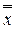 n) = f(x1, .., xn).
n) = f(x1, .., xn).
Предположим, что функция задана формулой. Можно ли найти по этой формуле двойственную функцию? Ответ на этот вопрос дает следующая теорема.
Дата добавления: 2016-03-27; просмотров: 866;
