Метод наибольшего правдоподобия.

Метод применяется при любой изменчивости стока. Результаты расчетов записываем в виде таблицы (табл. 1.5).

Таблица 1.5

Параметры кривой распределения годового расхода воды (Qi) рассчитанные методом наибольшего правдоподобия

№ члена ряда	Год	Qi, м³/с	Qiубыв, м³/с	P,%	ki=Qi/Q	lg ki	ki*lg ki
		8,34	14,00	2,78	1,87	0,272	0,509
		6,93	12,33	5,56	1,64	0,215	0,353
		6,2	12,23	8,33	1,63	0,212	0,346
		8,63	10,78	11,11	1,44	0,158	0,228
		6,5	10,4	13,89	1,39	0,143	0,199
		7,9	10,38	16,67	1,38	0,140	0,193
		12,33	8,95	19,44	1,19	0,076	0,014
		5,6	8,63	22,22	1,15	0,06	0,069
		8,95	8,34		1,11	0,045	0,049
		10,38	7,9	27,78	1,05	0,021	0,022
		10,78	7,9	30,56	1,05	0,021	0,022
		12,23	7,83	33,33	1,04	0,017	0,018
		7,06	7,77	36,11	1,04	0,017	0,018

Продолжение таблицы 1.5

№ члена ряда	Год	Qi, м³/с	Qiубыв, м³/с	P,%	ki=Qi/Q	Lg ki	ki*lg ki
		5,65	7,77	38,89	1,04	0,017	0,018
		7,51	7,51	41,67	1,001	0,0004	0,0004
		14,00	7,16	44,44	0,95	-0,022	-0,021
		4,7	7,06	47,22	0,94	-0,027	-0,025
		4,0	7,05		0,94	-0,027	-0,025
		6,43	6,93	52,78	0,92	-0,036	-0,033
		7,83	6,9	55,56	0,92	-0,036	-0,033
		5,28	6,74	58,33	0,9	-0,046	-0,041
		6,74	6,5	61,11	0,87	-0,06	-0,052
		4,29	6,43	63,89	0,86	-0,066	-0,057
		7,9	6,3	66,67	0,84	-0,076	-0,064
		6,23	6,23	69,44	0,83	-0,081	-0,067
		4,96	6,2	72,22	0,83	-0,081	-0,067
		4,73	5,65		0,75	-0,125	-0,094
		5,5	5,6	77,78	0,75	-0,125	-0,094
		7,16	5,5	80,56	0,73	-0,137	-0,100
		7,05	5,28	83,33	0,7	-0,154	-0,108
		6,9	4,96	86,11	0,66	-0,180	-0,119
		10,4	4,73	88,89	0,63	-0,200	-0,126
		6,3	4,7	91,67	0,63	-0,200	-0,126
		7,77	4,29	94,44	0,57	-0,244	-0,139
		7,77	4,00	97,22	0,53	-0,276	-0,146
Сумма		260,93			34,77	-0,785	0,521
Среднее		7,5

По данным таблицы на клетчатку вероятности наносим эмпирические точки и строим сглаженную эмпирическую кривую обеспеченности.

Определяем среднее многолетнее значение расхода воды:

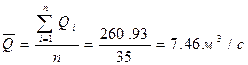
затем вычисляем суммы:

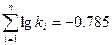
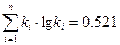
Для вычисления статистик 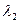и и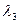спользуем формулы:

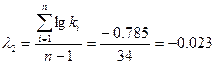
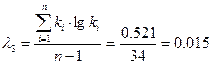
По специальным номограммам [2] определяем в соответствии с вычисленными статистикам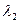и и 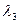коэффициент вариации 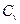=0.32 отношение . Затем по этим параметрам и 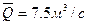, согласно таблице Ж.1 [2] вычисляем ординаты кривой трехпараметрического гамма - распределения и заносим в табл. 1.6.

Таблица 1.6

Ординаты аналитической кривой трехпараметрического гамма распределения

P, %	0,01	0,1									99,9
kp	2,66	2,29	1,89	1,58	1,43	1,19	0,95	0,77	0,54	0,41	0,29
Qp, м³/с	19,84	17,08	14,1	11,79	10,67	8,88	7,16	5,74	4,03	3,06	2,16

Определяем средние квадратические ошибки нормы годового стока и коэффициента вариации без учета автокорреляции по формулам:

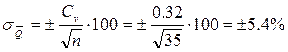
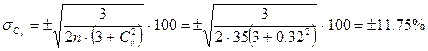
2) Метод моментов.

Применяется при изменчивости годового стока 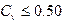. Расчет статистических параметров производим в порядке, указанном в табл. 1.7.

Таблица 1.7

Параметры кривой распределения годового расхода воды,

рассчитанные методом моментов

№ члена ряда	Год	Qi, м³/с	Qiубыв, м³/с	P,%	ki=Qi/Q	ki -1	(ki -1)²	(ki -1)³
		8,34	14,00	2,78	1,87	0,87	0,757	0,659
		6,93	12,33	5,56	1,64	0,64	0,410	0,262
		6,2	12,23	8,33	1,63	0,63	0,397	0,250
		8,63	10,78	11,11	1,44	0,44	0,194	0,085
		6,5	10,40	13,89	1,39	0,39	0,152	0,059
		7,9	10,38	16,67	1,38	0,38	0,144	0,055
		12,33	8,95	19,44	1,19	0,19	0,036	0,007
		5,6	8,63	22,22	1,15	0,15	0,023	0,004
		8,95	8,34		1,11	0,11	0,012	0,001
		10,38	7,90	27,78	1,05	0,05	0,003	0,0001
		10,78	7,90	30,56	1,05	0,05	0,003	0,0001
		12,23	7,83	33,33	1,04	0,04	0,0016	0,00006
		7,06	7,7	36,11	1,04	0,04	0,0016	0,00006
		5,65	7,7	38,89	1,04	0,04	0,0016	0,00006
		7,51	7,51	41,67	0,001	0,001	0,000001
		14,00	7,16	44,44	0,95	-0,05	0,003	-0,0001
		4,7	7,06	47,22	0,94	-0,06	0,004	-0,0002
		4,00	7,05		0,94	-0,06	0,004	-0,0002

Продолжение таблицы 1.7

№ члена ряда	Год	Qi, м³/с	Qiубыв, м³/с	P,%	ki=Qi/Q	ki -1	(ki -1)²	(ki -1)³
		6,43	6,93	52,78	0,92	-0,08	0,006	-0,0005
		7,83	6,90	55,56	0,92	-0,08	0,006	-0,0005
		5,28	6,74	58,33	0,90	-0,10	0,01	-0,001
		6,74	6,50	61,11	0,87	-0,13	0,017	-0,002
		4,29	6,43	63,89	0,86	-0,14	0,019	-0,003
		7,9	6,30	66,67	0,84	-0,16	0,026	-0,004
		6,23	6,23	69,44	0,83	-0,17	0,029	-0,005
		4,96	6,20	72,22	0,83	-0,17	0,029	-0,005
		4,73	5,65		0,75	-0,25	0,063	-0,016
		5,5	5,60	77,78	0,75	-0,25	0,063	-0,016
		7,16	5,50	80,56	0,73	-0,27	0,073	-0,02
		7,05	5,28	83,33	0,70	-0,30	0,09	-0,027
		6,90	4,96	86,11	0,66	-0,34	0,116	-0,039
		10,4	4,73	88,89	0,63	-0,37	0,137	-0,05
		6,3	4,70	91,67	0,63	-0,37	0,137	-0,05
		7,77	4,29	94,44	0,57	-0,43	0,185	-0,08
		7,77	4,00	97,22	0,53	-0,47	0,221	-0,01
Сумма		260,93			34,77		3,37	1,05
Среднее		7,46

Вычисляем смещенные значения коэффициентов вариации ( 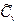), асимметрии ( 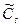) и средние квадратические ошибки по формулам:

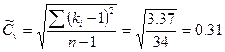
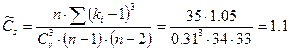
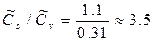
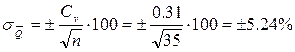
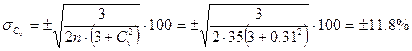
Относительная средняя квадратическая ошибка нормы годового расхода воды 5.24%<10% (продолжительность периода n=35 лет) считается достаточной.

Расчетные несмещенные значения коэффициентов ( 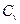) и ( 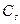) для биноминального распределения методом моментов определяется по [2], где коэффициенты и 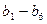найдены по табл. 4.1[2] для соотношения 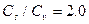и коэффициента автокорреляции r(1)=0:

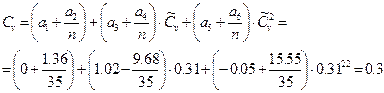
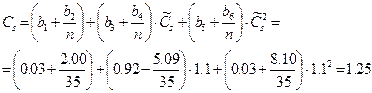
По несмещенным параметрам 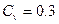, 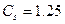и 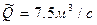вычисляем ординаты биноминальной кривой распределения (табл. 1.8) по таблице К.1[2].

Таблица 1.8

Ординаты аналитической кривой биноминального распределения годового стока (для метода моментов)

P, %	0,01	0,1									99,9
Фр	6,55	4,9	3,19	1,93	1,34	0,51	-0,2	-0,74	-1,22	-1,41	-1,52
kp=Фр*Cv+1	2,97	2,47	1,96	1,58	1,4	1,15	0,94	0,78	0,63	0,58	0,54
Qp, м³/с	22,28	18,53	14,70	11,85	10,5	8,63	7,05	5,85	4,73	4,35	4,05

По данным табл.1.8 на клетчатке вероятности строим аналитическую кривую биноминального распределения модулей годового стока, с которой снимаются искомые значения годового стока заданной вероятности превышения.

123 4

Дата добавления: 2016-03-27; просмотров: 589;