Магнитоэлектрические приборы
Устройство. Магнитоэлектрические приборы (МЭП) состоят из ИЦ, ИМ и ОУ
(см. рис.2.1) Конструктивно измерительный механизм может быть выполнен либо с подвижным магнитом, либо с подвижной катушкой. На рис. 2.2 показана конструкция прибора с подвижной катушкой.
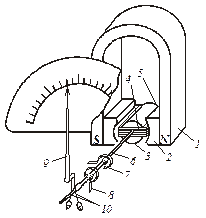
Рис.2.2. Устройство магнитоэлектрического прибора.
Постоянный магнит 1, магнитопровод с полюсными наконечниками 2 и неподвижный сердечник 3 составляют магнитную систему механизма. В зазоре между полюсными наконечниками и сердечником создается сильное равномерное радиальное магнитное поле, в котором находится подвижная прямоугольная катушка 4, намотанная медным или алюминиевым проводом на алюминиевом каркасе (применяют и бескаркасные рамки). Катушка (рамка) может поворачиваться в зазоре на полуосях 5 и 3. Спиральные пружины 7 и 8 создают противодействующий момент и используются для подачи измеряемого тока от выходных зажимов прибора в рамку (механические и электрические соединения на рисунке не показаны) Рамка жестко соединена со стрелкой 9. Для балансировки подвижной части имеются передвижные грузики 10.
Принцип действия.Проходя по проводникам обмотки рамки, ток I взаимодействует с магнитным потоком постоянного магнита, что вызывает появление механических сил F, создающих вращающий момент Мвр для рамки. Из теоретических основ электротехники известно выражение для механической работы, совершаемой при перемещении проводника с током в магнитном поле:
F dα = dWМ ,
где F— сила, действующая на проводник в направлении элементарного перемещения dα; dWМ - изменение запаса энергии магнитного поля.
Если проводник движется по окружности с радиусом r, то
dx=r dα,,
где dα — элементарный угол поворота.
Следовательно,
Fdα=dWМ .
Здесь Fr— вращающий момент - МВР, т. е.
МВР dα = dWМ .
Тогда окончательно запишем:
МВР = dWМ / dα. (2.1)
Это уравнение является обобщенным выражением вращающего момента для всех приборов, в которых используют сила электромагнитного поля
Противодействующий момент в приборах необходим для создания однозначного соответствия измеряемой величины определенному углу отклонения подвижной части. В аналоговых электромеханических приборах противодействующий момент создается либо при помощи спиральных пружин (растяжек и подвесов), либо за счет энергии электромагнитного поля (в логометрах).
В случае, когда противодействующий момент создается спиральной пружинкой
МПР = W·α, (2.2)
где W – удельный противодействующий момент, зависящий от геометрических размеров и материала пружины (растяжек)
Уравнение шкалы.Выражение для вращающего момента, действующего на рамку при протекании по ней тока I, может быть получен, исходя из обобщенного выражения вращающего момента (2.1). Запас электромагнитной энергии в контуре с током I, находящемся в поле постоянного магнита, выражается формулой:
WМ = І·Ψ,
где Ψ— полное потокосцепление данного контура с магнитным полем постоянного магнита. Тогда
МВР = Ι·dΨ / dα. (2.3)
При повороте рамки на угол dα каждая ее сторона опишет дугу dα·b/2, пересекая при этом силовые линии магнитного поля; число пересеченных линий будет равно произведению пройденного пути dα·b/2 на длину активной стороны рамки l и на индукцию в зазоре В.
Полное изменение потокосцепления с рамкой равно произведению числа силовых линий, пересеченных обеими сторонами рамки, на число витков ее обмотки, т. е.
dΨ = 2·Βlω dα·b/2,
где ω - число витков обмотки.
Произведение·Βl равно площади рамки; обозначив еечерез S,получим:
dΨ =BSωdα.
Если положить dα =1 рад, то произведение BSω - величина постоянная для каждого данного прибора - будет равна изменению потокосцепления при повороте рамки на 1 рад. Обозначая его через Ψ0, запишем:
Ψ0 = BSω [вб/рад], (2.4)
Тогда
dΨ = Ψ0 · dα. (2.5)
Подставляя выражение (2.5) формулу (2.3), получим выражение вращающего момента для магнитоэлектрического механизма в следующем виде:
МВР = Ι · Ψ0. (2.6)
Установившееся положение подвижной катушки наступает при равенстве вращающего и противодействующего моментов? МВР = МПР, т.е. с учетом (2.2) запишем:
Ι ·Ψ0 = W·α. (2.7)
Отсюда находим уравнение шкалы измерительного механизма магнитоэлектрической системы
α = Ι · Ψ0 / W
или
α = S · Ι, (2.8)
где величина S = Ψ0 / W является чувствительностью прибора (в радианах на ампер).
Используя выражение (2.4) можно ввести в уравнение шкалы конструктивные параметры измерительного механизма:
α = Bsω Ι · 1/W, (2.9)
т.е. угол отклонения подвижной части прямо пропорционален току в рамке, поэтому магнитоэлектрические приборы имеют равномерные шкалы.
Успокоение подвижной части магнитоэлектрических приборов магнитоиндукционное, т.е. создается взаимодействием магнитных полей от вихревых токов в каркасе рамки и поля постоянного магнита.
Метрологические характеристики MЭП: классы точности – 0,05; 0,1 и т.д., равномерная шкала, высокая и стабильная чувствительность, малое собственное потребление мощности, большой диапазон измерений, большой МВР, успокоение только магнитоиндукционное.
Эксплуатационные характеристики: возможность использования только в цепях постоянного тока, малая нагрузочная способность, сложны и дороги, на показания прибора влияет температура, но не влияют внешние магнитные и электрические поля.
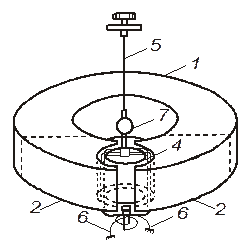 |
Гальванометры постоянного тока. На рис. 2.5 показано устройство магнитоэлектрического гальванометра постоянного тока. Сильный постоянный магнит 1 из высококоэрцетивного сплава, полюсные наконечники 2 из магнитомягкой стали с
Рис. 2.5. Устройство магнитоэлектрического гальванометра.
цилиндрической расточкой концов, неподвижный стальной цилиндр 3 , укрепленный в расточке, служат для создания в зазоре сильного равномерного магнитного поля. В этом зазоре находится рамка 4,укрепленная на подвесе 5; ток подводится через безмоментные спирали 3. На оси рамки закреплено зеркальце 7 для оптического отсчета угла отклонения рамки от нулевого положения.
На рамку, при подаче тока I действуют моменты: вращающий МВР (2.6), успокоения МУ = − Р dα/dt, направленный в сторону, противоположную МВР. и противодействующий момент, создаваемый при закручивании подвеса МПР = Wα.
Величина P = Ψ0 / (RГ + RВН) называется коэффициентом успокоения и определяется конструктивными параметрами гальванометра Ψ0, RГ и сопротивлением внешней цепи RВН. Изменяя RВН можно изменять коэффициент успокоения.
 |
Известно, что движение вращающегося тела определяется уравнением
где J – момент инерции тела; d2α/dt2 – угловое ускорение; ΣM – сумма вращающих моментов, действующих на тело.
 |
Для гальванометра это уравнение имеет вид:
 |
Подставляя в уравнение (2.15) значения моментов с учетом их знака получим дифференциальное уравнение движения подвижной рамки гальванометра:
Интеграл этого дифференциального уравнения второго порядка с постоянными коэффициентами и с правой частью, как известно, состоит из двух членов: αС –частного решения при заданных условиях и α0 – общего решения данного уравнения без правой части, т.е.
α = αС + α0 (2.17)
Частное решение уравнения (2.16), рассмотренное для случая установившегося равновесия подвижной части гальванометра, когда скорость ее движения (dα/dt ) и ускорение (d2α/dt2) будут равны нулю, через выражение (2.7) получим
αс = S1 × I (2.18)
Уравнение (2.16) без правой части для получения общего решения имеет вид:
 |
 |
Решением его будет функция
Где С1 и С2 постоянные интегрирования, получаемые из начальных условий; Х1 и Х2 – корни характеристического уравнения
JX2 + PX + W = 0 (2.21)
Нахождение этих корней и подстановка их в выражение (2.19) и далее полученного значения α0 в (2.17) дает искомое уравнение движения подвижной части гальванометра:
α = F(t) (2.22)
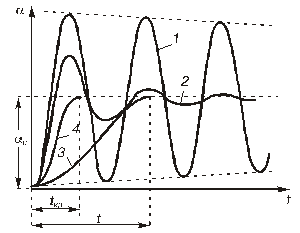 |
График функции (2.22) для различных значений сопротивления нагрузки приведен на рис.2.3.
Рис.2.3. Режимы движения подвижной части гальванометра.
При RВН = ∞ колебания подвижной части гальванометра будут постепенно, хотя и медленно, затухать из-за трения подвижной рамки о воздух (кривая 1) и режим движения рамки - колебательный.
При RКР < RВН < ∞ подвижная часть совершает затухающие колебательные движения около положения установившегося равновесия, определяемого углом αс (кривая 2)
При RВН < RКР режим движения рамки гальванометра будет апериодическим (кривая 3).
При Rвн = Rкр подвижная часть приходит в режим устойчивого равновесия без колебаний и за минимальное время (кривая 4). Этот режим называется критический.
Значение критического сопротивления Rкр предопределяет возможность применения гальванометра и его всегда указывают на шкале прибора.
Метрологические характеристики: чувствительность, период собственных колебаний, внешнее и полное критическое сопротивление.
Применение: для измерения малых токов и напряжений, в качестве нуль индикаторов.
Дата добавления: 2016-03-22; просмотров: 3171;
