Диагностирование электровозов в системе их технического обслуживания и ремонта

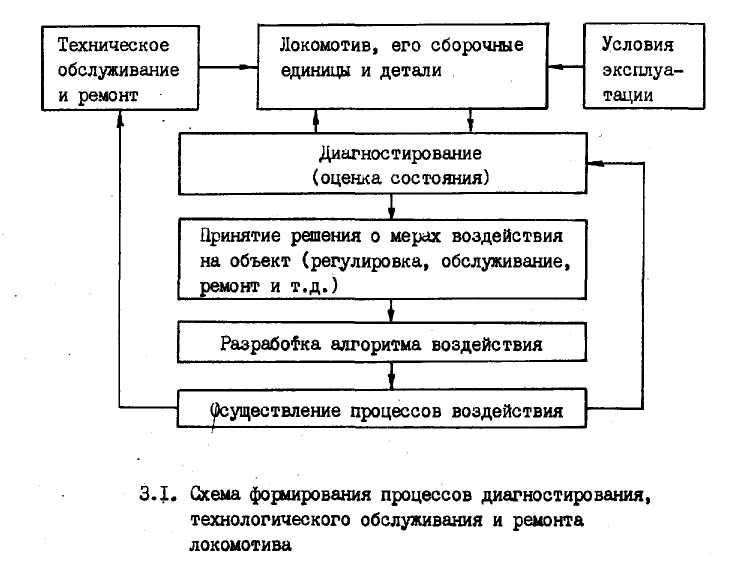
На рис. 3.1. представлена структурная схема формирования процес­сов диагностирования и технического обслуживания и ремонта локомо­тивов. Как видно объект диагностирования - электровоз находятся с одной стороны под разрушающим воздействием условия эксплуатации, а с другой стороны под восстанавливающим воздействием технического обслуживания и ремонта. Поэтому техническое состояние электровоза может постоянно меняться и характеризуется законами изме­нения параметров технического состояния и диагностических параметров,

а также законами распределения показателя надёжности его сборочных единиц и деталей в функции от времени или пробега. Экономические показатели характеризуются затратами трудовых, материальных, топлив­но-энергетических и финансовых ресурсов на диагностирование, обслуживание и ремонт. В связи с тем, что процессы формирования системы диагностирования, технического обслуживания и ремонта локомотивов связаны в единый ком­плекс, методически удобно рассматривать его не только с точки зрения физических характеристик, но и как математические модели описания их изменений в процессе эксплуатации электровозов.

Разработка и создание системы технического диагностирования бази­руется на изучении объекта (узла или детали электровоза). Их возможных отказов, признаков этих отказов и включает в себя построение и анализ математических моделей, математическая модель объекта диагностирова­ния представляет формальное описание объекта в исправном состоя­нии в виде детерминированных или вероятностных зависимостей воздействиями на объект и его реакциями на эти воздейст­вия.

При построении математических моделей принято обозначать симво­лом Х _m - мерный вектор, компонентами которого являются значе­ния переменных величин на входе объекта, характеризующих восприни­маемые им воздействия х ₁ , х _{2 , …..,} х _m.

Аналогично обозначают У _П - мерный вектор п параметров технического состояния или иначе внутренних структурных параметров У1, У2, …Уп, a Z обозначают z - мерный вектор значения z диагностических параметров на выходе объекта или иначе выходных функций Z1, Z2,…..Zz на,...н«.

Запись 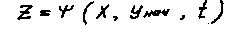(3.1)

может обозначать аналитическую, векторную, табличную или другую форму представления системы передаточных функций исправного объекта диагностирования, отражающих зависимость реализуемых выходных функ­ций Z от входных переменных X , начального значения Унач внутренних переменных и времени (наработки) t.

Система ( 3.1) является математической моделью исправного объекта. Можно выделить для рассмотрения конечное множество 3 воз­можных неисправностей объекта. При наличии в объекте неисправности

SiCS , i=1,2….., / S / говорят, что он находится в i - неисправном состоянии или является i - неисправным. Объект, нахо­дящийся в i - неисправном состоянии, реализует систему передаточных функций

(3.2)

представленных в той же форме, что и передаточные функции (3.1). Система (3.2) для фиксированного i является математической мо­делью i - неисправного объекта.

Система (3.1) и совокупность систем (3.2) для всех SiCS образует модель объекта диагностирования. Часто в явном виде задаёт­ся только модель исправного объекта, т.е. зависимость (3.1), а пове­дение объекта в i- неисправных состояниях задаётся косвенно, че­рез множество S возможных неисправностей (неявная модель объекта).

Показатели динамики изменения параметров деталей и сборочных еди­ниц локомотивов в эксплуатации находят по результатам измерений и статистической обработки полученных данных. Отклонение значения струк­турного параметра (параметра состояния объекта) от номинала выра­жается случайной функцией:

(3.3)

где

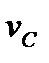- показатель случайной скорости отклонения параметра
при наработке t=1 , уменьшенной в L- раз (ед.параметра/ед.наработки);

t - наработка ( ч, км, ткм и т.д.);

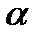- показатель степени, характеризующий кривизну реали­заций на всём диапазоне их измерения;

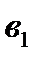- показатель приработки детали (в ед. параметра);

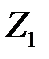- стационарная случайная функция отклонения параметра с

нулевым математическим ожиданием (в ед. параметра).

При выборе диагностических параметров деталей и сборочных единиц локомотивов в результате анализа статистических рядов значений структурных и диагностических параметров находят по каждому струк- турному параметру функцию его математического ожидания

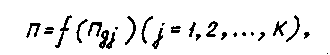(3.4)

Где

- величины структурного и j -го диагностического параметров.

Затем с помощью критерия тесности связи - коэффициента z ус­танавливают корреляционную зависимость между j -м диагностичес­ким параметром и структурным. Диагностические параметры, для которых z мал, исключают. Для остальных рассчитывают значения обобщащего показателя связи:

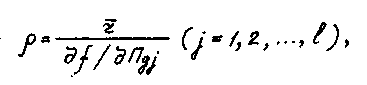(3.5)

где

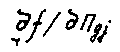
- частная производная функция в точке, ордината

которой равна допускаемому значению параметра;

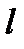- число оставшихся исследуемых диагностических параметров.

Большие значения обобщающего показателя служат в пользу выбора данного диагностического параметра.

На железных дорогах действует планово-предупредительная система технического обслуживания и ремонта локомотивов (ТО и Р). Ремонтный цикл состоит из ремонтов разного объёма, следующих друг за другом с определенной периодичностью.

Номенклатура ТО и ТP для электровозов установлена приказом Министра путей сообщения № 2В Ц от 2и июня 1986 года.