ОБЩИЕ ПОНЯТИЯ. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ВЕРОЯТНОСТЕЙ

Наиболее важные показатели надежности невосстанавливаемых объектов – показатели безотказности, к которым относятся:

· вероятность безотказной работы;

· плотность распределения отказов;

· интенсивность отказов;

· средняя наработка до отказа.

Показатели надежности представляются в двух формах (определениях):

Ø статистическая (выборочные оценки);

Ø вероятностная.

Статистические определения (выборочные оценки) показателей получаются по результатам испытаний на надежность.

Допустим, что в ходе испытаний какого-то числа однотипных объектов получено конечное число интересующего нас параметра – наработки до отказа. Полученные числа представляют собой выборку некоего объема из общей «генеральной совокупности», имеющей неограниченный объем данных о наработке до отказа объекта.

Количественные показатели, определенные для «генеральной совокупности», являются истинными (вероятностными) показателями, поскольку объективно характеризуют случайную величину – наработку до отказа.

Показатели, определенные для выборки, и, позволяющие сделать какие-то выводы о случайной величине, являются выборочными (статистическими) оценками. Очевидно, что при достаточно большом числе испытаний (большой выборке) оценки приближаются к вероятностным показателям.

Вероятностная форма представления показателей удобна при аналитических расчетах, а статистическая – при экспериментальном исследовании надежности.

Для обозначения статистических оценок будем использовать знак сверху.

Примем следующую схему испытаний для оценки надежности.

Пусть на испытания поставлено N одинаковых серийных объектов. Условия испытаний идентичны, а испытания каждого из объектов проводятся до его отказа.

Введем следующие обозначения:

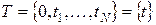– случайная величина наработки объекта до отказа;

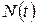– число объектов, работоспособных к моменту наработки t;

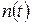– число объектов, отказавших к моменту наработки t;

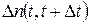– число объектов, отказавших в интервале наработки ;

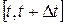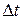– длительность интервала наработки.

Поскольку в дальнейшем определение выборочных оценок базируется на математических моделях теории вероятностей и математической статистики, то ниже приводятся основные (минимально необходимые) сведения из теории вероятностей.

С более подробным материалом из теории вероятностей студенты могут ознакомиться в Приложении: «Основные понятия и краткие сведения из теории вероятностей».

2.2 Основные сведения о математических моделях расчета в теории вероятностей

Теория вероятностей – математическая наука, изучающая закономерности в случайных явлениях.

Основные понятия теории множеств

Одним из основных понятий является – случайное событие.

Событием называется всякий факт (исход), который в результате опыта (испытания) может произойти или не произойти.

Каждому из таких событий можно поставить в соответствие определенное число, называемое его вероятностью и являющееся мерой возможного совершения этого события.

Теория вероятностей основывается на аксиоматическом подходе и опирается на понятия теории множеств.

Множество – это любая совокупность объектов произвольной природы, каждый из которых называется элементом множества.

Предположим, что производится некоторый опыт (испытание), результат которого заранее неизвестен. Тогда множество W всех возможных исходов опыта представляет пространство элементарных событий, а каждый его элемент 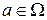(отдельный исход опыта) является элементарным событием. Любой набор элементарных событий (любое их сочетание) считается подмножеством (частью) множества W и является случайным событием, т.е. любое событие А – это подмножество множества W: .

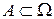В общем случае, если множество W содержит n элементов, то в нем можно выделить 2ⁿ подмножеств (событий).

Введем ряд определений.

Совместные (несовместные) события – такие события, появление одного из которых не исключает (исключает) возможности появления другого.

Зависимые (независимые) события – такие события, появление одного из которых влияет (не влияет) на появление другого события.

Противоположное событие относительно некоторого выбранного события А – событие, состоящее в не появлении этого выбранного события (обозначается ).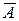

Полная группа событий – такая совокупность событий, при которой в результате опыта должно произойти хотя бы одно из событий этой совокупности.

Дата добавления: 2016-03-20; просмотров: 728;