Занятие 6. Электромагнитные волны. Излучение электромагнитных волн 3 страница

На рис. 9.7 изображена примерная графическая зависимость векторовнапряжённостей E_Z+ электрическоговдоль OZ оси и H_X+ магнитноговдоль OX оси полей плоской электромагнитной волны, бегущейв положительную сторону OY оси, от y координатыв момент

t₁ = T/4 времени.

Промежуток T времени,за котороеплоская(рис. 9.3) из раздела 9.0 "Электромагнитные волны. Излучение" бегущая электромагнитная волнапреодолеваетс фазовойcскоростью в вакууме расстояние, равное λдлине волны,называют периодом колебаний электромагнитной волны.

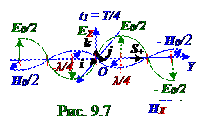
OZ оси и H_X магнитноговдоль OX оси полей, находящаяся в момент t₀ = 0 времени (рис.9.4) в

O координате, переходит (рис.9.7) за промежуток T/4 времени по OY оси в y = λ/4координату.

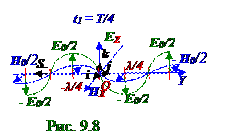
OY осиэлектромагнитная волна преодолеваетс фазовойcскоростью в вакууме расстояние, равное λ/4длине волны, т.е. плоскость равных фазэтойплоской(рис. 9.3) из раздела 9.0 "Электромагнитные волны. Излучение" бегущей электромагнитной волныс максимумами векторов напряжённостей E_Z электрическоговдоль OZ оси и H_X магнитноговдоль OX оси полей, находящаяся в момент t₀ = 0 времени (рис. 9.5) в O координате, переходит (рис.9.8) за промежуток

T/4 времени по OY оси в y = - λ/4координату.

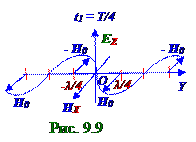
разность фаз колебанийвекторанапряжённости H_X магнитногополя вдоль OX оси (рис. 2.19) из раздела 2.0 "Колебания и волны" равна 2π.

Согласно графическому сложению бегущих плоских электромагнитных волнв (4.1), (4.2) положительную (рис. 9.7) ив (4.4), (4.5) отрицательную (рис.9.8) стороны OY оси приводит к (рис. 9.9) отсутствию в момент t₀ = T/4 времени вектора E_Z напряжённости электрическогополя вдоль OZ осиплоской стоячей электромагнитной волны.

Графическое сложение бегущих плоских электромагнитных волнв (4.1), (4.2) положительную (рис. 9.4) ив (4.4), (4.5) отрицательную (рис.9.5) стороны OY оси приводит к наличию в момент t₀ = T/2 времени вектора E_Z напряжённости электрическогополя вдоль OZ осиплоской стоячей электромагнитной волны,изменяющегосяпо (4.7) уравнению, и имеет графическую (рис.9.6) зависимость.

Графическое сложение бегущих плоских электромагнитных волнв (4.1), (4.2) положительную (рис.9.4) ив (4.4), (4.5) отрицательную (рис. 9.5) стороны OY оси приводит к наличию в момент t₀ = 3T/4 времени вектора E_Z напряжённости электрическогополя вдоль OZ осиплоской стоячей электромагнитной волны,изменяющегосяпо (4.8) уравнению, и имеет графическую (рис.9.9) зависимость.

Таким образом, в моменты t_n = n(T/2) времени, где n = 0, 1, 2, ….,плоская стоячая электромагнитная волна представляет собой (рис. 9.6) вектор E_Z напряжённости электрическогополя вдоль OZ оси, изменяющийся в зависимости от y координатыпо (4.7) выражению. Вектор напряжённости H_X магнитногополя вдоль OX оси в эти моменты t_n = n(T/2) времени, где

n = 0, 1, 2, …., отсутствует, т.е. H_X = 0.

В моменты t_n = T/4 + n(T/2) времени, где n = 0, 1, 2, ….,плоская стоячая электромагнитная волна представляет собой (рис. 9.9) вектор напряжённости H_X магнитногополя вдоль OX оси, изменяющийся в зависимости от y координатыпо (4.8) выражению.

Вектор E_Z напряжённости электрическогополя вдоль OZ оси в эти моменты

t_n = T/4 + n(T/2) времени, где n = 0, 1, 2, …., отсутствует, т.е. E_Z = 0.

У плоской стоячей электромагнитной волныв O координат, т.е. при y₀ = 0, вектор

E_Z напряжённости электрическогополя (4.7) зависит от tвремени в соответствии со следующим уравнением: E_Z = E₀cosky₀cosωt = E₀cosωt = E₀cos(2π/T)t, (4.9)

т.е. в O координат вектор E_Z напряжённости электрическогополя в зависимости от tвременипринимает значения от -E₀ до E₀ с модулем, равным E₀ амплитуде этого вектора E_Z напряжённости электрическогополя.

Вектор E_Z напряжённости электрическогополя в зависимости от tвремениу плоской стоячей электромагнитной волны принимает значения от -E₀ до E₀ с модулем, равным E₀ амплитуде этого вектора E_Z напряжённости электрическогополя, на OY оси при y_n = 0, ± λ/2, ± λ, …, т.е.при

y_n = ± nλ/2, где n = 0, 1, 2, …., поскольку в (4.9) имеет место следующее соотношение:

cosky_n = cos(2π/λ)y_n = ± 1. (4.10)

Поэтому при y_n = ± nλ/2, где n = 0, 1, 2, …., вектор E_Z напряжённости электрическогополя имеет пучностьсвоегозначения.

Вектор E_Z напряжённости электрическогополя в зависимости от tвремениу плоской стоячей электромагнитной волны принимает значения, равное нулю, на OY оси при

y_n = ± λ/4, ± 3λ/4, …, т.е.при y_n = ± λ(1 + 2n)/4, где n = 0, 1, 2, …., поскольку в (4.9) имеет место следующее соотношение: cosky_n = cos(2π/λ)y_n = 0. (4.11)

Поэтому при y_n = ± λ(1 + 2n)/4, где n = 0, 1, 2, …., вектор E_Z напряжённости электрическогополя имеет узелсвоегозначения.

Результирующее E_Z (y, t) уравнение, по которому изменяется вектор E_Z напряжённостиэлектрического поля плоской стоячей электромагнитной волны в сечении с y координатой в произвольныймоментtвремени определяется суперпозицией бегущих плоских электромагнитных волнв (2.69) из раздела 2.0 "Колебания и волны" (4.1) положительную и(2.72) из раздела 2.0 "Колебания и волны" (4.2) отрицательнуюстороны OY оси, вследствие чего проекция E_Z на OZ ось координат этого вектора напряжённости E_Z электрического поля стоячей электромагнитной волны вдоль OZ оси имеет следующий вид:

E_Z = E_Z+ + E_{Z -} = (E₀/2)cos(ωt - ky) + (E₀/2)cos(ωt + ky) = E₀cos(ωt)cos(ky). (4.12)

Поскольку вектор напряжённости E_Z электрического поля стоячей электромагнитной волны имеет только проекцию E_Z на OZ ось координат, то в векторномвиде (4.12) имеет следующий вид: E_Z = E₀ cos(ωt)cos(ky), (4.13) где E₀ = kE₀ - вектор амплитуды напряжённостиэлектрического поля плоской стоячей электромагнитной волны, а k - орт декартовой системы координат по OZ оси.

Результирующее H(y, t) уравнение, по которому изменяется векторынапряжённости

H_X магнитногополя вдоль OX плоской стоячей электромагнитной волны в сечении с y координатой в произвольныймоментtвремени определяется суперпозицией бегущих плоских электромагнитных волнв (2.69) из раздела 2.0 "Колебания и волны" (4.2) положительную и(2.72) из раздела 2.0 "Колебания и волны" (4.5) отрицательнуюстороны OY оси, вследствие чего проекция H_X на OX ось координат этого векторанапряжённости H_X магнитногополявдоль OX оси плоской стоячей электромагнитной волны имеет следующий вид:

H_X = H_X+ + H_X- = (H₀/2)cos(ωt - ky) - (H₀/2)cos(ωt + ky) = H₀sin(ωt)sin(ky). (4.14) Поскольку вектор напряжённости H_Xмагнитного поля плоской стоячей электромагнитной волны имеет только проекцию H_X магнитногополя, то в векторномвиде (4.14) имеет следующий вид: H_X= H₀ sin(ωt)sin(ky), (4.15) где H₀ = iH₀ - вектор амплитуды напряжённостимагнитного поля плоской стоячей электромагнитной волны, а i - орт декартовой системы координат по OX оси.

Согласно (4.15) вектор напряжённости H_Xмагнитного поля плоской стоячей электромагнитной волны в зависимости от tвремениу плоской стоячей электромагнитной волны принимает значения, равное нулю, на OY оси при y_n = 0, ± λ/2, ± λ …, т.е.при y_n = ± nλ/2,

где n = 0, 1, 2, …., поскольку в (4.9) имеет место следующее соотношение: sinky_n = sin(2π/λ)y_n = 0. (4.16)

Поэтому при y_n = ± nλ/2, где n = 0, 1, 2, …., вектор напряжённости H_Xмагнитного поля плоской стоячей электромагнитной волны имеет узелсвоегозначения. Вектор напряжённости H_Xмагнитного поля в зависимости от tвремениу плоской стоячей электромагнитной волны принимает значения от -H₀ до H₀ с модулем, равным H₀ амплитуде этого вектора напряжённости H_Xмагнитного поля, на OY оси при y_n = ± λ/4, ± 3λ/4, …, т.е.при

y_n = ± λ(1+ 2n)/4, где n = 0, 1, 2, …., поскольку в (4.15) имеет место следующее соотношение:

sinky_n = sin(2π/λ)y_n = ± 1. (4.17)

Поэтому при y_n = ± λ(1+ 2n)/4, где n = 0, 1, 2, …., вектор E_Z напряжённости электрическогополя имеет пучностьсвоегозначения.

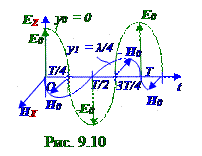
поля вдоль OZ оси по t времени (рис. 9.10) смещены относительнопучностей векторанапряжённости H_Xмагнитного поля вдоль OX оси на величину T/4, гдеT - период колебаний электромагнитной волны, а на OY оси эти пучности вектора E_Z напряжённости электрического вдоль OZ оси смещены относительнопучностей векторанапряжённости H_Xмагнитного поля вдоль OX оси на величину λ/4, гдеλ- длина электромагнитной волны.

Уплоской стоячей электромагнитной волны(рис. 9.10) согласно (4.13) и (4.15) нулевые значения, т.е.узлы вектора E_Z напряжённости электрическогополя вдоль OZ оси существуют на

OY оси при y_n = ± λ(1 + 2n)/4 в моменты t_n = T/4 + n(T/2) времени, а нулевые значения, т.е.узлы вектора напряжённости H_Xмагнитного поля вдоль OX оси существуют на OY оси при y_n = ± nλ/2 в моменты t_n = n(T/2) времени, где n = 0, 1, 2, …..

Таким образом,узлы вектора E_Z напряжённости электрическогополя вдоль OZ оси по t времени (рис. 9.10) смещены относительноузлов векторанапряжённости H_Xмагнитного поля вдоль OX оси на величину T/4, гдеT - период колебаний электромагнитной волны, а на OY оси эти узлы вектора E_Z напряжённости электрического вдоль OZ оси смещены относительноузлов векторанапряжённости H_Xмагнитного поля вдоль OX оси на величину λ/4, гдеλ- длина электромагнитной волны.

Задача 9.5

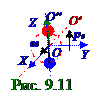
положительный заряды диполя.Найти среднюю <P> мощность излучения данногоэлектрического диполя.Дано: p_e, ω / P = ?

Вращение вектора p_e дипольного электрического момента (5.61) из раздела 5.1 "Электрическое поле системы неподвижных зарядов в вакууме. ТеоремаГауссадля электростатического поля. Работа и потенциал электростатического поля" с вектором ω угловой скорости вокруг OO′ оси, которая перпендикулярна OO′′ оси электрического диполя и проходит черезсередину прямой линии,соединяющейотрицательный и положительныйзаряды диполя, на рис. 9.12 осуществлено сложением двух векторов p_e дипольного электрического момента. Каждый издвух (рис. 9.12) векторов p_e1, p_e2 дипольного электрического момента существует вследствие наличия двух электрическихдиполей. Электрический дипольс 1- ым номером представляет собой (9.87) из раздела 9.0 "Электромагнитные волны. Излучение" неподвижный точечный положительныйзаряди колеблющийся около него по OY оси с циклической ω частотой отрицательныйзаряд. Вектор p_e1дипольного электрического момента электрического диполя

(рис. 9.11)с 1- ым номером будет зависеть от tвременипо следующему уравнению гармонических колебаний: p_e1= kp_mcosωt, (5.1)

где p_m - амплитудноезначение вектора p_e1дипольного электрического момента электрического диполяс 1- ым номером, которое имеет место при смещении точечного отрицательногозарядана (рис. 9.12) максимальное l_m расстояние относительно неподвижного точечного положительного зарядавверх или вниз поOZ оси; k - единичныйвектор (1.1) из раздела 1.0 "Физические основы механики" по OZ оси.

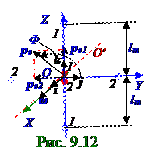
момента электрического диполяс 2- ым номером, которое имеет место при смещении точечного отрицательногоq_- зарядана (рис. 9.11) расстояние l_m относительно неподвижного точечного положительногозарядавправо или влево по OX оси; i - единичныйвектор (1.1) из раздела 1.0 "Физические основы механики" по OX оси.

Результирующий вектор p_eдипольного электрического момента от двух электрических диполей равен сумме векторов p_e1, p_e2 дипольных электрических моментов электрических диполейс 1- ым и 2- ым номерами, вследствие чего выражение результирующего вектора p_eдипольного электрического момента с учётом (5.1), (5.2) имеет следующий вид: p_e =p_e1 + p_e2 = -jp_msinωt +kp_mcosωt.(5.3)

В начальный t₀ = 0 момент временимодульp_e результирующего вектора p_eдипольного электрического момента от двух электрических диполей равен согласно (5.3) равен p_m амплитудномузначению вектора p_e1дипольного электрического момента электрического диполяс 1- ым номером, а направлен этот результирующий вектор p_eдипольного электрического момента по OZ оси в соответствии с условием (рис. 9.11) данной задачи.

Проекции p_eY, p_eZ результирующего вектора p_eдипольного электрического момента от двух электрических диполейсогласно (5.3) соответственно на OY, OZ оси имеют следующий вид:

p_eY = -p_msinωt; p_eZ = p_mcosωt.(5.4)

Модуль p_e (2.18) из раздела 2.0 "Колебания и волны" и (рис.9.11) Ф фаза(2.19)из раздела 2.0 "Колебания и волны" с учётом (5.4) значений проекций p_eY, p_eZ результирующего вектора

p_eдипольного электрического момента от двух электрических диполейимеют следующий вид:

p_e = (p_eY² + p_eZ²)^1/2= p_m; Ф = arctg(p_eZ/p_eY) = arctg(- ctgωt)= arctg{tg[(π/2) + ωt]} = [(π/2) + ωt]. (5.5)

Согласно (5.5) результирующий (рис. 9.12) вектор p_eдипольного электрического момента от двух электрических диполейимеет постоянное значение p_eмодуля, а модуль ω вектора ω угловой скорости, с которой этот вектор вращается против часовой стрелки вокруг OO′ оси, тоже постоянен и соответствует условию задачи. Поэтому вращающийся вокруг OO′ оси электрический диполь

(рис.9.11) с постоянным модулем p_e вектора p_e дипольного электрического момента и с постоянным вектором ω угловой скорости можно заменить суммой двух электрических диполей, каждый из которых представляет собой неподвижный точечный положительныйзаряд сколеблющимися около него по OX, OY осям с циклическойω частотой отрицательнымизарядами.

Среднее (рис.9.12) из раздела 9.0 "Электромагнитные волны. Излучение" значение < P > мощности P излучения, т.е. количествоэнергии, переносимой в среднем за Δt интервалвремени электромагнитнойволной через всю сферическую поверхность S площадью r радиуса, вызванное колеблющимся с циклическойω частотой электрическим диполем в волновойзоне этого электрического диполя, т.е. с r радиусом сферической поверхности S площадью много больше

(рис. 9.12) максимальногоl_m расстояния между неподвижным точечным положительнымзарядом сколеблющимся около него с циклическойω частотой отрицательнымзарядом, с учётом (9.98) из раздела 9.0 "Электромагнитные волны" имеет следующий вид: <Р> = ω⁴p_m ²/2πεε₀v³,(5.6)

где v = 1/(εε₀μμ₀)^1/2 - фазовая скоростьэлектромагнитнойволны в среде с εдиэлектрической проницаемостью и с μмагнитной проницаемостью.

Среднее значение <P>₀ мощности P₀ излучения от (рис. 9.12) двух электрических диполей, которые имеют одинаковые параметры, кроме направлений векторов p_e1, p_e2 дипольных электрических моментов, дающих в сумме результирующий вектор p_eдипольного электрического момента от одного вращающегося электрического диполя, в 2 - ва раза больше среднего (5.6) значения <P> мощности P излучения от одногоэлектрического диполя, вследствие чего среднее значение <P>₀ мощности P₀ излучения от двух электрических диполей имеет следующий вид:

<P>₀ = 2<Р> = ω⁴p_m ²/6πεε₀v³.(5.7)

Задача 9.6

В волновой зоне электрического диполя в вакууме,имеющегоось поOZ оси, на

r₀ расстоянии от него в направлениимаксимальногоизлучения по OY оси амплитуда вектора

E_Z напряжённости электрическогополя вдоль OZ оси убегущих электромагнитных волнравна E_0m.

Найти <S> среднеезначение плотности потокаэнергии, переносимой бегущей электромагнитнойволной, т.е. среднее<S> значениеS модуля вектораSПойнтингаэтой электромагнитнойволны, на r > r₀ расстоянии в направлении, составляющем θ угол полярного расстояния с осью электрического диполя, равным 30°. Дано: r₀, E_0m, r, θ/<S> = ?

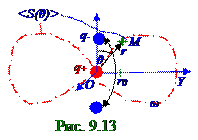
относительно неподвижного q₊ положительного точечного заряда; p_Zm - проекция (9.87) из раздела 9.0"Электромагнитные волны" наOZ ось амплитудногозначения вектора электрического моментадиполя; c² = 1/ε₀μ₀ - квадратскорости светав вакууме (9.9) из раздела 9.0 "Электромагнитные волны. Излучение".