Занятие 6. Электромагнитные волны. Излучение электромагнитных волн 1 страница

Задача 9.1, №№ 9-16

Плоская гармоническая электромагнитная волна распространяется в вакууме в положительном направлении OY оси. Вектор S(y, t) плотности потока электромагнитной энергии имеет следующий вид: S = S_mcos²(wt - ky).Считая k волновое число и амплитудное S_m значение вектора S плотности потока электромагнитной энергии известными и действительными величинами, что допустимо для однородной изотропной среды без эффектов поглощения с известными постоянными ε диэлектрической, μмагнитной проницаемостями, найти:

1) вектор E(y, t)напряжённости электрического поля этой волны как функцию t времени и y координат точки наблюдения;

2) вектор H(y, t) напряжённости магнитного поля этой волны как функцию t времени и y координат точки наблюдения;

3) объёмную w(y, t) плотность энергии как функцию t времени и y координат точки наблюдения;

4) средний áSñ вектор Пойнтинга;

5) среднее значение áSñ плотности потока энергии, переносимой этой волной;

6) вектор j_см плотности тока смещения;

7) среднее á j_см ñ за T период колебаний электромагнитной волны значение модуля плотности тока смещения;

8) величину импульса K_ед электромагнитной волны в единице объёма вакуума, если в нём распространяется электромагнитная волна;

9) записать волновое уравнение для магнитной и электрической компонент рассматриваемой электромагнитной волны и изобразить схематично мгновенную фотографию этой волны.

Дано:S = S_mcos²(wt - ky), k, ε, μ, S_m/E(y, t)=?, H(y, t) = ?, w(y, t) =?, áSñ =?, áSñ =?, j_см =?, á j_см ñ =?, K_ед =?, волновые уравнения =?, мгновенная фотография =?.

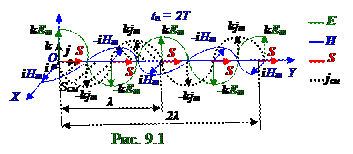
где E_m = kE_Zm - вектор (9.30) из раздела 9.0 "Электромагнитные волны. Излучение"амплитуды напряжённости электрическогополя, а E_Zm - проекция на OZ ось напряжённости электрическогополя в y координате по OY оси и в t время, когда эта напряжённостьотклоняетсяот O координат на максимальное значение, т.е. принимает E_m , "- E_m" значения; H_m =iH_Xm - вектор (9.31) из раздела 9.0 "Электромагнитные волны"амплитуды напряжённости магнитногополя, а H_Xm - проекция на OX ось напряжённости магнитногополя в y координате по OY оси и в t время, когда эта напряжённостьотклоняетсяот O координат на максимальное значение, т.е. принимает H_m , "- H_m" значения.

Согласно (9.26) из раздела 9.0 "Электромагнитные волны. Излучение " колебания векторов напряжённостей E_Zэлектрическогополя вдоль OZ оси и H_Xмагнитногополя вдоль OX осипроисходят в одной фазеили синфазно, поэтому E_Zm , H_Xm - проекции векторов напряжённостейсоответственнона OZ ось электрическогои на OX осьмагнитногополей меняют свой знак одновременно и их произведение всегда положительно,поэтому оно заменено произведением E_mH_m амплитуд электрическогои магнитногополей, а (1.1) вектор S(y, t) плотности потока электромагнитной энергии направлен (рис.9.1) по OY оси.

Согласно (9.1) и (рис.9.1), а также (9.32) из раздела 9.0 "Электромагнитные волны. Излучение векторы напряжённостей E электрическогополя и H магнитногополя в произвольной y координате по OY оси и произвольное t время имеют следующий вид: E =kE_mcos(ωt - ky).(1.2)

H = iH_mcos(ωt - ky). (1.3)

С учётом (9.28) из раздела 9.0 "Электромагнитные волны. Излучение" отношения E_m/H_m амплитуд колебаний векторов напряжённостей E электрического и Hмагнитногополей выражение (1.3) принимает следующий вид: H = i(ε₀ε/μ₀μ)^1/2E_mcos(ωt - ky). (1.4)

Подставляем (1.4), (1.2) в (1.1) и получаем следующее выражение E_m амплитуды векторанапряжённости E электрическогополя электромагнитной волны:

[kE_mcos(ωt - ky)i(ε₀ε/μ₀μ)^1/2E_mcos(ωt - ky)] = jS_mcos²(wt - ky) ↔ [ki](ε₀ε/μ₀μ)^1/2E_m²cos²(wt - ky) = = jS_m cos²(wt - ky) ↔ E_m =S_m ^1/2 (μ₀μ/ε₀ε) ^1/4 . (1.5)

Подставляем (1.5) в (1.4) и получаем следующее выражение H_m амплитуды векторанапряжённости H магнитногополя электромагнитной волны:

H = i(ε₀ε/μ₀μ)^1/2S_m ^1/2(μ₀μ/ε₀ε) ^1/4 cos(ωt - ky) ↔ H_m = (ε₀ε/μ₀μ) ^1/4S_m ^1/2 , (1.6)

где ε, μ-постоянные диэлектрическаяи магнитнаяпроницаемости среды, в которой распространяется электромагнитная волна.

Подставляем (1.5) в (1.2), а также подставляем (1.6) в (1.3) и получаем следующие выражения векторов E(y, t), H(y, t) напряжённостейсоответственно электрическогои магнитногополей в электромагнитной волне как функцию t времени и y координат точки наблюдения:

E = k(μ₀μ/ε₀ε) ^1/4 S_m ^1/2cos(ωt - ky).(1.7) H = i(ε₀ε/μ₀μ)^1/2 S_m ^1/2cos(ωt - ky). (1.8)

3) Объёмная (9.36) из раздела 9.0 "Электромагнитные волны. Излучение" w плотность энергии электромагнитной волныс учётом модулей E, H векторов E(y, t), H(y, t) напряжённостейсоответственно (1.7), (1.8) электрическогои магнитногополей в электромагнитной волне как функцией t времени и y координаты точки наблюдения имеет следующий вид:

w = (1/v)EH = (1/v)|(μ₀μ/ε₀ε) ^1/4 S_m ^1/2cos(ωt - ky)| |(ε₀ε/μ₀μ)^1/2 S_m ^1/2cos(ωt - ky)| = (S_m/v)cos²(wt - ky), (1.9)

где v = 1/(ε₀εμ₀μ)^1/2 - фазовая скорость электромагнитнойволны в среде с постоянными ε диэлектрической и μмагнитной проницаемостями.

4) Среднее áSñ значение вектора Пойнтинга за Δt интервал времени с учётом Δt >>T = 2π/ω, где ω -циклическая частота(9.24) из раздела 9.0 "Электромагнитные волны. Излучение" гармонических колебаний с T периодом векторов напряжённостей E_Z электрическогополя вдоль OZ оси и H_Xмагнитногополя вдоль OX оси (рис. 9.4) из раздела 9.0 "Электромагнитные волны. Излучение" электромагнитнойволны в произвольной y координате точки наблюдения в однородной изотропной среды без эффектов поглощения имеет следующий вид:Δt Δt wΔt- ky

áSñ = ∫[S_mcos²(wt - ky)dt/Δt] = (S_m/Δt) ∫ cos²(wt - ky)dt = (S_m/Δtw)∫cos²zdz =

0 0 - ky

= (S_m/Δtw){[(z/2)] + [(1/4)sin2 z]}| ^{wΔt- ky} _{- ky} = (S_m/Δtw)(1/2){wΔt+ (1/2)[sin2(wΔt - ky)+ sin2ky]}= = (S_m/Δtw)(1/2){wΔt+[sinwΔt cos(wΔt - ky)]} = (S_m/Δtw)(1/2){(2π/T)Δt+[sinwΔt cos(wΔt - ky)]} ≈ S_m/2,(1.10)

где z = wt- ky; dt = dz/w; z₁ = - ky; z₂ =wΔt- ky; |sinwΔt cos(wΔt - ky)| ≤ 1, а (2π/T)Δt = Δtw >>1, т.к. Δt >>T, т.е. интервал Δt времени вычисления среднего áSñ значение вектора Пойнтинга много больше T периода гармонических колебаний векторов напряжённостей E_Z электрическогополя вдоль OZ оси и H_Xмагнитногополя вдоль OX оси электромагнитнойволны.

5) Среднее á S ñ значение (9.37) из раздела 9.0 "Электромагнитные волны. Излучение" модулявектора S Пойнтинга - этоколичество энергии, переносимой электромагнитнойволной через поверхность, перпендикулярную направлению распространения электромагнитнойволны и равной единичнойплощади, за единицу t времени. Эта величина является постоянной величиной, т.е. не зависит от момента t времени, если этот момента t временинаходится в Δt интервале временивычисления среднего áSñ значение вектора Пойнтинга, имеет с учётом (1.10) следующий вид:

á S ñ = S_m/2,(1.11)

где S_m - амплитудное значение вектора S плотности потока электромагнитной энергии, переносимой электромагнитнойволной.

6) Вектор j_смплотности(рис.9.1) тока смещения (8.77) из раздела 8.0 "Электромагнитная индукция. УравненияМаксвелладля электромагнитного поля"-это изменяющееся во t времениэлектрическое полес векторомD электрического смещения(5.87)из раздела 5.2 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля", который имеет с учётом (1.7) следующий вид: j_см= (∂D/∂t) ↔ j_см= = ε₀ε∂E/∂t = -k ε₀ε(μ₀μ/ε₀ε) ^1/4ωS_m ^1/2sin(ωt - ky) = -k(μ₀μ)^1/4/ε₀ε)^3/4ωS_m ^1/2sin(ωt - ky). (1.12)

Вектор j_смплотности(рис.9.1) тока смещения(1.12)сравнительно с (1.7) изменяет своё направление, модуль в произвольной y координате точки наблюдения электромагнитнойволны, распространяющейся в однородной изотропной среде без эффектов поглощения, в соответствии с гармонической функцией и в зависимости от времени сонаправлен или противонаправлен k единичному вектору по OZ оси, т.е. сонаправлен или противонаправлен вектору E напряженности электрического поля(5.3) из раздела 5.1 "Электрическое поле системы неподвижных зарядов в вакууме. ТеоремаГауссадля электростатического поля. Работа и потенциал электростатического поля" электромагнитнойволны

7) В начале 0 координат (рис.9.1), т.е. при y = 0 в (1.12), вектор j_смплотноститока смещения электромагнитнойволны в течение T периода гармонических колебаний векторов напряжённостей E_Z электрическогополя вдоль OZ оси и H_Xмагнитногополя вдоль OX оси меняет своё направление в соответствии со следующей гармонической функцией: j_см= -k (μ₀μ)^1/4/ε₀ε)^3/4ωS_m ^1/2sinωt (1.13)

Среднее á j_см ñ значение за T период колебаний электромагнитной волны с учётом равенства S_см площадей, ограниченных (рис.9.1) за T/2 полпериод колебаний электромагнитной волны функцией (1.13) j_сммодуля плотности тока смещения, имеет следующий вид:

T/2 T/2 T/2

á j_см ñ = (2/T) ∫| j_см|dt = [2(μ₀μ)^1/4/ε₀ε)^3/4ωS_m ^1/2 /T] ∫sinωtdt= [2(μ₀μ)^1/4/ε₀ε)^3/4ωS_m ^1/2 /T] ∫sin(2πt/T)dt =

0 0 0

= [2(μ₀μ)^1/4/ε₀ε)^3/4(2π/T)S_m ^1/2 ν](T/2π) [-cos(2πt/T)]| ^T/2₀ = 4(μ₀μ)^1/4/ε₀ε)^3/4S_m ^1/2 ν,(1.14) где ν = 1/T - частота гармонических колебаний с T периодом векторов напряжённостей

E_Z электрическогополя вдоль OZ оси и H_Xмагнитногополя вдоль OX оси электромагнитнойволны.

8) С учётом (9.62) из раздела 9.0 "Электромагнитные волны. Излучение" сонаправленности вектора K_ед.обимпульса, передаваемого плоской электромагнитнойволной в вакууме проводнику единичного объёма в единицу времени, вектору SПойнтингаэтот вектор K_ед.обимпульса с учётомвыражениявектора S = S_mcos²(wt - ky) плотности потока электромагнитной энергии, заданного в условии,имеет следующий вид: K_ед.об. = S/c² = S_mcos²(wt - ky)/c² ↔ S = c² K_ед.об, (1.15)

где c² = 1/ε₀μ₀ - квадратскорости электромагнитной волныв вакууме.

Вектор SПойнтинга(9.39) из раздела 9.0 "Электромагнитные волны. Излучение" сонаправлен (1.15) вектору K_ед.обимпульса, поэтомумодуль K_ед.об (9.61) из раздела 9.0 "Электромагнитные волны" вектора K_ед.об.импульса, передаваемого плоской электромагнитнойволной проводнику единичного объёма в единицу времени, пропорционален модулю S вектора SПойнтингаплотности потокаэнергии, переносимой электромагнитнойволной, и с учётом(1.9) объёмной w плотности энергии электромагнитной волныэтотмодуль K_ед.об имеет следующий вид:

K_ед.об. = S/c² = S_mcos²(wt - ky)/c² = w/c, (1.16)

где S_mcos²(wt - ky) - модуль вектора S = S_mcos²(wt - ky) плотности потока электромагнитной энергии, переносимой электромагнитнойволной и заданной в условии.

9) Частныйслучай (9.21). (9.23) из раздела 9.0 "Электромагнитные волны. Излучение" трёхмерных волновыхуравнений, справедливых для плоской электромагнитной волны, котораяраспространяется в нейтральной, непроводящейсреде с постоянными ε диэлектрической, μмагнитной проницаемостями, в которой равняется нулюρ плотность свободныхзарядов, т.е. ρ= 0, и равняется нулю вектор j = 0 плотноститоков проводимости, т.е. j = 0, имеет следующий вид:

∂²E_Z/∂y² = εμ(∂²E_Z/∂t²)/c² (1.17)

∂²H_X/∂y ² = εμ(∂²H_X/∂t²)/c² . (1.18)

Простейшим решением одномерных волновыхуравнений (1.17), (1.18) является следующая гармоническаязависимость проекций E_Z, H_X на OZ, OX оси координат соответственно векторов напряжённостей E_Z электрическогои H_X магнитногополя от tвремении y координаты: E_Z = E_mcos(ωt - ky+ φ₁) (1.19) H_X = H_mcos(ωt - ky+ φ₂),(1.20)

где ω -циклическая частотаколебаний векторов напряжённостей E_Z электрическогополя вдоль OZ оси и H_Xмагнитногополя вдоль OX оси; k = ω/v (2.70)из раздела 2.0 "Колебания и волны"- волновое число, v = с/(εμ)^1/2- фазоваяскорость плоской электромагнитной волны; E_m и H_m - амплитуды колебаний векторов напряжённостейсоответственно E_Z электрическогополя вдоль OZ оси и H_Xмагнитногополя вдоль OX оси; φ₁ и φ₂ - начальные фазыколебанийвекторовнапряжённостейсоответственно E_Z электрическогополя вдоль OZ оси и H_Xмагнитногополя вдоль OX оси.

Задача 9.2

Цилиндрическийнерелятивистский протонный пучокрадиуса r₀ распространяется в свободном пространстве. Протоны пучка m_p массой и p_e зарядом летят параллельно, их кинетическаяэнергия равна W_kp, а концентрация равна n. Найти модуль S и направление вектора S Пойнтингавнутрии вне протонного пучкана r, rрасстоянии от его оси.

Дано: r₀, m_p, p_e, W_kp, n/S(r) = ?

Поскольку протоны(рис.9.2) распространяются с вектором v_p нерелятивистскойскорости, то v_p модуль их скорости с учётом заданной W_kp кинетической(1.88) из раздела 1.0 "Физические основы механики" имеет следующий вид: v_p = (2W_kp /m_p)^1/2 м/с. (2.1) Согласно (6.7) из раздела 6.0 "Электрический ток" теории электронной проводимости модуль jвектора j плотноститока, который образован цилиндрическимнерелятивистским протонным пучкомрадиуса r₀ с границами, изображёнными на рис.6.2 красными штриховымилиниями, с учётом (2.1) имеет следующий вид: j = np_ev_p = np_e(2W_k /m_p)^1/2 А/м², (2.2) где m_p, p_e, v_p, n и W_kp - соответственно масса, p_e заряд, модуль v_p вектора v_p нерелятивистскойскорости, концентрация и кинетическая энергияпротонов.

Замкнутаяповерхность воображаемогоцилиндра l длиной, r₁ радиусом (рис.9.1.2) и V₁ = πr₁ ²l объёмом этого воображаемогоцилиндра, находящегося в нерелятивистском протонном пучке, охватывает движущиеся протоны, общий зарядq_p1 которых с учётом их концентрации n и заряда p_e одного протонаимеет следующий вид: q_p1 = p_enV₁ = p_enπr₁²l А·с, (2.3)

где r₁ ≤ r₀.

Векторы E₁', E₁'' ….напряжённостиэлектрического поляпредставляют собой цилиндрическое векторное поле инаправленыперпендикулярно боковойповерхностивоображаемогоцилиндра r₁ радиуса F₁ = 2πr₁l площадью, находящегося в нерелятивистском протонном пучке, т.е. направлены по радиальным силовым линиям напряжённостиэлектрического поля, которые на рис.9.2 изображены точками. Задача определения модуляE₁ вектора E₁ напряжённостиэлектрического поляв нерелятивистском протонном пучке, т.е при r₁ < r₀ , аналогична(1.7)из 5.2 семинара "Проводники и диэлектрики в электрическом поле", в которой определяется модуль E вектора E напряжённостиэлектростатического поля внутри цилиндрического конденсатора.

		Различие с (1.7)из 5.2 семинара "Проводники и диэлектрики в электрическом поле" заключается в равенстве единице относительнойдиэлектрической εпроницаемости в нерелятивистском протонном пучкеи в отличие общего зарядаqp1 движущихся протонов, охватываемых воображаемымцилиндром l длинойи r1 радиусом (рис.9.1.2) с площадью боковойповерхностиэтоговоображаемогоцилиндра F1 = 2πr1l площадью, от погонногоq0 заряда (рис. 5.2) из 5.2 семинара "Проводники и диэлектрики в электрическом поле" на внутреннейобкладке цилиндрического конденсатора. МодульE1 вектора E1 напряжённостиэлектрического поляв нерелятивистском протонном пучкеимеетс учётом (2.3) следующий вид: E1F1= qp1 /ε0 ↔ E12πr1l = penπr12l/ε0↔ ↔ E1 = penr1/2ε0кг·м/А·с3(В/м), (2.4)где r1 ≤ r0.

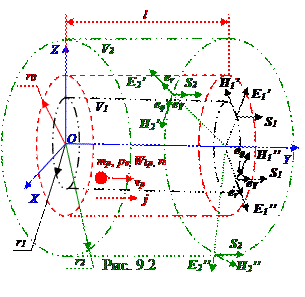Замкнутая поверхность воображаемогоцилиндра l длинойи r₂ радиусом (рис. 9.2), находящаяся за пределами нерелятивистского протонного пучка, охватывает все движущиеся протоны в цилиндре r₀ радиусаи объёмом V₂ = πr₀²lэтого воображаемогоцилиндра, общий зарядq_p2 которых с учётом их концентрации n и заряда p_e одного протонаимеет следующий вид:

q_p2 = p_enV₂ = p_enπr₀²l А·с. (2.5)МодульE₂ вектора E₂ напряжённостиэлектрического поляза пределами нерелятивистского протонного пучкапо аналогии с (2.4) с учётом того, что общий заряд(2.5)q_p2 движущихся за пределами этого нерелятивистского протонного пучка протонов охватывается (рис. 09.1.2) воображаемымцилиндром l длиной и r₂ радиусом с F₂ = 2πr₂l площадью боковойповерхностиэтоговоображаемогоцилиндра, имеетследующий вид:

E₂F₂= q_p2 /ε₀ ↔ E₂2πr₂l = p_enπr₀²l/ε₀↔ E₂ = p_enr₀²/2r₂ε₀кг·м/А·с³(В/м).(2.6) где r₂ ≥ r₀. Результирующийток проводимости I_рез1силой (рис. 9.2) через основание воображаемого цилиндра с r₁ радиусом и площадью N₁ = πr₁², находящегося в нерелятивистском протонном пучке, с учётом (2.2) модуля jвектора j плотноститока в этом цилиндрическомнерелятивистском протонном пучкеимеет следующий вид:I_рез1 = jN₁ = jπr₁ ² = np_e(2W_k /m_p)^1/2πr₁ ² А, (2.7) где r₁ ≤ r₀. Векторы H₁', H₁'' …напряжённостиполямагнитного поля представляют собой цилиндрическое векторное поле инаправленыпо касательной к силовым линиям напряжённостимагнитного поля, которые имеют форму окружности r₁ радиуса, L₁ = 2πr₁ длиной и изображены на

рис. 9.2 чёрнымилиниями штрихс двумя точками. Задача определения модуляН₁ вектора H₁ напряжённостимагнитного поляв нерелятивистском протонном пучке, т.е при r₁ < r₀ аналогична(1.3) из 7.2.1 семинара "Постоянное магнитное поле", в которой определяется модуль Hвекторанапряжённости H магнитного поля в функции от радиуса rокружности, охватывающей кольцевуюповерхность магнетика с внутреннимR радиусоми внешнимr радиусом. Различие с (1.3) из 7.0 семинара "Постоянное магнитное поле" заключается в равенстве единицеотносительнойμмагнитной проницаемостив нерелятивистском протонном пучкеи в отличие результирующеготока проводимости I_рез1 силой (рис. 9.2) через основание воображаемого цилиндра с r₁ радиусом и площадью N₁ = πr₁², находящегося в нерелятивистском протонном пучке, отрезультирующеготока проводимости I_рез силой (1.2) из 7. 0 семинара"Постоянное магнитное поле" через поверхностькольца с внутреннимR радиусом и внешнимr радиусом.