Занятие 6. Электромагнитные волны. Излучение электромагнитных волн 2 страница
МодульH1 вектора H1 напряжённостимагнитного поляв нерелятивистском протонном пучкеимеетс учётом (2.7) следующий вид:
H1L1 = Iрез1 ↔ H12πr1 = npe(2Wk /mp)1/2πr1 2↔ H1 = nper1(Wk /2mp)1/2 А/м, (2.8) где r1 ≤ r0. Результирующийток проводимости Iрез2 силой (рис. 9.2) через основание воображаемого цилиндра с r2 радиусом и N2 = πr22 площадью, находящегося за пределами нерелятивистского протонного пучкаи поэтому включающего все движущиеся протоны через основание цилиндра с r0 радиусом и N0 = πr02 площадью, с учётом (2.2) модуля jвектора j плотноститока в цилиндрическомнерелятивистском протонномпучке этот результирующийток проводимости Iрез2 силой будет иметь следующий вид:Iрез2 = jN0 = jπr0 2 = npe(2Wk /mp)1/2πr0 2 А. (2.9) МодульH2 вектора H2 напряжённостимагнитного поляза пределами нерелятивистского протонного пучкапо аналогии с (2.8) с учётом того, чтосиловые линии напряжённостимагнитного поля, которые имеют форму окружности r2 радиуса, длиной L2 = 2πr2 и изображены на рис. 09.1.2 зелёными линиями штрихс двумя точками, охватывают(2.9) результирующийток проводимости
Iрез2 силой, поэтому этот модульH2 вектора H2 напряжённостимагнитного поля имеет следующий вид: H2L2 = Iрез2 ↔ H22πr2 = npe(2Wk /mp)1/2πr0 2 ↔ H2 = npe r0 2(Wk /2mp)1/2πr2 А/м,(2.10) где r2 ≥ r0. Векторы E1, E2 ….напряжённостиэлектрического поля (рис.6.2) внутри и за пределами нерелятивистского протонного пучкапредставляют собой цилиндрическое векторное полеи направлены по er орту радиальной полярной координаты.
Векторы H1, H2 …напряжённостиполямагнитного поля (рис.9.2) внутри и за пределами нерелятивистского протонного пучкапредставляют собой цилиндрическое векторное полеи направлены по eφ орту угловой полярной координаты.
Вектор S1 Пойнтинга(9.39) из раздела 9.0 "Электромагнитные волны. Излучение" с учётом (2.4) модуляE1 вектора E1 напряжённостиэлектрического поля, а также с учётом (2.8) модуляH1 вектора H1 напряжённостимагнитного поляв нерелятивистском протонном пучке имеют следующий вид: S1 = [E1, H1] = [E1er, H1eφ] = [(penr1/2ε0)er,nper1(Wk /2mp)1/2eφ] =
= (penr1/2ε0)[nper1(Wk /2mp)1/2] ex = [n2 pe 2 r1 2(2Wk /mp)1/2/4ε0]eY, (2.11) где eY- орт в цилиндрическойсистеме координат, направленный по OY оси и составляющий с
er ортом радиальной полярной координаты, eφ ортом угловой полярной координатыправовинтовуюсистему, т.е. eY= [er, eφ]; r1 ≤ r0.
МодульS1 вектора S1 Пойнтинга, направленного вдоль OY оси, в нерелятивистском протонном пучке согласно (2.11)имеет следующий вид:
S1 = n2 pe 2 r1 2(2Wk /mp)1/2/4ε0 кг/с3 (Вт/м2),(2.12) где r1 ≤ r0.
Вектор S2 Пойнтинга(9.39) из раздела 9.0 "Электромагнитные волны. Излучение" с учётом (2.6) модуляE2 вектора E2 напряжённостиэлектрического поля, а также с учётом (2.10) модуляH2 вектора H2 напряжённостимагнитного поляза пределами нерелятивистского протонного пучка имеют следующий вид: S2 = [E2, H2] = [E2er, H2eφ] = [(penr02/2r2ε0 )er,npe r0 2(Wk/2mp)1/2πr2 eφ] = = (penr02/2r2ε0)[nper0 2(Wk /2mp)1/2πr2]ex = [n2pe 2r04(2Wk/mp)1/2/4ε0r22] eY,(2.13) где eY- орт в цилиндрическойсистеме координат, направленный по OY оси и составляющий с er ортом радиальной полярной координаты, eφ ортом угловой полярной координатыправовинтовуюсистему, т.е. eY= [er, eφ]; r2 ≥ r0.
МодульS2 вектора S2 Пойнтинга, направленного вдоль OY оси, за пределами нерелятивистского протонного пучка согласно (2.13)имеет следующий вид: S2 = n2pe 2r04(2Wk/mp)1/2/4ε0r22 кг/с3 (Вт/м2).(2.14)
где r2 ≥ r0.
Согласно (9.37) из раздела 9.0 "Электромагнитные волны. Излучение" и выражениям (2.12), (2.14) с их размерностями модули S1, S2 вектора S1, S2 Пойнтингаравняются количеству энергии, переносимой в нерелятивистском протонном пучкеи соответственно за его пределами через поверхность, перпендикулярную направлению распространения этого нерелятивистского протонного пучка и равную единичнойплощади, за единицу t времени.
Задача 9.3
В вакууме вдоль OY оси распространяются две плоскиеодинаково поляризованные бегущиеэлектромагнитные волны, векторы E1, E2 напряжённостиэлектрического полякоторыхизменяютсяпо следующим уравнениям сгармоническими функциями: E1 = E0cos(ωt - ky) и E2 = E0cos(ωt - ky + φ), где E0 = kE0 - вектор амплитуды каждой из плоских бегущихэлектромагнитных волн, а k - орт декартовой системы координат по OZ оси; φ - начальная фаза колебаний вектора E2 напряжённостиэлектрического полявторой электромагнитной волны.
Найти <S> среднеезначение плотности потокаэнергии, переносимой электромагнитнойволной, т.е среднее<S> значениеS модуля вектораSПойнтингаэтой электромагнитнойволны.
|
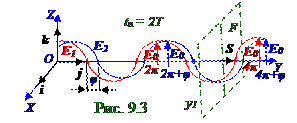
В плоскости площади F, ориентированной перпендикулярно, например, в y1 координате существуютодинаково направленныегармонические колебаний векторов E1, E2 напряжённостиэлектрического поля электромагнитной волны.Результирующийвектор Eр колебаний напряжённостиэлектрического поляпо аналогии с (2.17) из раздела 2.0 "Колебания и волны" определится сложениемдвуходинаково направленныхгармонических колебаний векторов
E1, E2 напряжённостейэлектрического поля электромагнитной волны. С учётом тригонометрическоготождества результирующийвектор Eр колебанийнапряжённостиэлектрического поля двуходинаково направленныхпоk орту гармонических колебаний векторов
E1, E2 напряжённостейэлектрического поля электромагнитной волны имеет следующий вид:
Eр = E0k[cos(ωt - ky1) + cos(ωt - ky1 + φ)] = 2E0 k {cos[2(ωt - ky1) + φ]/2}cos(φ/2), (3.1) где E0 = E0 = E0 - одинаковая амплитуда гармонических колебаний векторов E1, E2 напряжённостиэлектрического поля первой и второй электромагнитной волны.
Вектор Hр результирующегоколебания в y1 координате напряжённостимагнитногополя согласно (9.24) из раздела 9.0 "Электромагнитные волны. Излучение" направлен (рис.9.3) вдоль OX оси и совпадает с направлением единичного i орта. С учётом (3.1) вектор Hр результирующегоколебания в координате y1 напряжённостимагнитногополя электромагнитной волны имеет следующий вид: Hр = H0i[cos(ωt - ky1) + cos(ωt - ky1 + φ)] = 2H0i{cos[2(ωt - ky1) + φ]/2}cos(φ/2), (3.2) где H0 = H0 = H0 - одинаковая амплитуда гармонических колебаний векторов H1, H2 напряжённостиэлектрического поля первой и второй электромагнитной волны.
Согласно (9.29) из раздела 9.0 "Электромагнитные волны. Излучение" отношение E0/H0амплитуд колебаний векторов E0 напряжённостей(9.24) из раздела 9.0 "Электромагнитные волны" электрическогополя вдоль OZ оси и H0 магнитногополя вдоль OX оси электромагнитной волны для вакуума имеет следующий вид: E0/H0 = (μ0/ε0)1/2 кг·м2/А2с2. (3.3) С учётом (9.10) из раздела 9.0 "Электромагнитные волны. Излучение"равенства в вакууме v скорости электромагнитной волнскорости с = 1/(ε0 μ0)1/2 светавыражение(3.3) для H0амплитуды результирующего колебания вектора H0 (10.23) магнитногополя электромагнитной волны принимает следующий вид: H0 = ε0сE0 А/м . (3.4) С учётом направленности вектора Hр результирующегоколебания напряжённостимагнитногополя электромагнитной волны в y1 координате по OX оси с единичным i ортом, а также с учётом (3.4) выражение (3.2) вектора Hр результирующегоколебания в y1 координате напряжённостимагнитногополя электромагнитной волны принимает следующий вид: Hр = 2ε0сiE0 {cos[2(ωt - ky1) + φ]/2}cos(φ/2). (3.5) С учётом направленности вектора Eр результирующегоколебаниянапряжённости электрическогополя электромагнитной волны в y1 координате по OZ оси с единичным k ортом выражение (3.1) вектора Eр результирующегоколебания в y1 координате напряжённостиэлектрическогополя электромагнитной волны принимает следующий вид: Eр = 2kE0 {cos[2(ωt - ky1) + φ]/2}cos(φ/2).(3.6) Вектор S Пойнтинга(9.39) из раздела 9.0 "Электромагнитные волны. Излучение" для(3.6) вектораEр результирующегоколебания в y1 координате напряжённости электрическогополя электромагнитной волныи (3.5) вектора Hр результирующегоколебания в y1 координате напряжённостимагнитного поля этой же электромагнитной волны(рис.9.3) имеет следующий вид: S = [Eр,Hр] = 4ε0с[ik]E0 2{cos2 [2(ωt - ky1) + φ]/2}cos2 (φ/2). (3.7) С учётом равенства в (3.7) векторного [ik] произведения единичному j орту, направленному (рис. 9.3) из раздела 9.0 "Электромагнитные волны. Излучение" вдоль OY оси,модуль S вектора SПойнтинга(3.7) равняется количеству энергии, переносимой результирующейэлектромагнитной волнойв направлении OY оси через поверхность F площадью, перпендикулярную направлению распространения этой результирующейэлектромагнитной волны, расположенную в y1 координате и равную единичнойплощади, за единицу t времени, и имеет следующий вид:
S = 4ε0сE0 2{cos2 [2(ωt - ky1) + φ]/2}cos2(φ/2) кг/с3 (Вт/м2). (3.8) Среднее <S> значение модуля S (3.8) вектора SПойнтинга(рис.9.3), т.е. среднеезначение плотности потокаэнергии, переносимой результирующей электромагнитнойволной в направлении OY осичерез поверхность F площадью, перпендикулярную направлению распространения этой результирующейэлектромагнитной волны, расположенную в y1 координате и равную единичнойплощади, за Δt интервал времени, например (рис. 9.4) из раздела 9.0 "Электромагнитные волны. Излучение", равный периоду T колебаний электромагнитной волны, определяется из следующего выражения: T <S> = 4ε0сE0 2cos2(φ/2) {∫ {cos2 [2(ωt - ky1) + φ]/2}dt}/T. (3.9) 0 В выражении (3.9) при вычислении интеграла применяется (9.24) из раздела 9.0 "Электромагнитные волны. Излучение" соотношение ω=2π/T междуωциклическойчастотойиT периодом колебаний электромагнитной волны, вследствие чего значение этого интеграла принимает следующий вид: T ∫ {cos2 [2(ωt - ky1) + φ]/2}dt}/T = 1/2. (3.10) 0 Подставляем (3.10)в (3.9) с учётом тригонометрического cos2(φ/2) = (1+ cosφ)/2 тождества и получаем следующее среднее <S> значение модуля S вектора SПойнтинга, т.е. среднеезначение плотности потокаэнергии, переносимого результирующей электромагнитнойволной в направлении OY осичерез поверхность F площадью, перпендикулярную направлению распространения этой результирующейэлектромагнитной волны, расположенную в y1 координатеи равную единичнойплощади, за Δt интервал времени:<S> = ε0сE0 2(1+ cosφ) кг/с3 (Вт/м2).(3.11)
Задача 9.4
В вакууме вдоль OY оси установилась плоская стоячая электромагнитная волна, вектор
E напряжённостиэлектрического полякоторыхизменяетсяпо следующему уравнению
E = E0coskycosωt, где E0 = kE0 - вектор амплитуды напряжённостиэлектрического поля стоячей электромагнитной волны, а k - орт декартовой системы координат по OZ оси. Изобразить примерный график распределения векторов E напряжённостиэлектрического поляи H напряжённостимагнитного полястоячей электромагнитной волныв зависимости от y координаты в моменты
t0 = 0, t1 = T/4 времени.Найти H(y, t) уравнение, по которому изменяется вектор H напряжённостимагнитного полястоячей электромагнитной волны. Дано: E = E0coskycosωt/Примерный график = ?H(y, t) = ?
Результирующие E(y, t),H(y, t) уравнения, по которым изменяются векторы E напряжённостиэлектрического поля,H индукциимагнитного полястоячей электромагнитной волны в сечении с
y координатой в произвольныймоментtвремени определяется (2.122) из раздела 2.0 "Колебания и волны" суперпозицией бегущих плоских электромагнитных волнв (2.69) из раздела 2.0 "Колебания и волны" положительную и(2.72) из раздела 2.0 "Колебания и волны" отрицательнуюстороны OY оси.
Проекции EZ+, HX+ на OZ, OX оси координат (9.24) из раздела 9.0 "Электромагнитные волны. Излучение" соответственно векторов напряжённостей EZ+ электрическогои HX+ магнитногополя, в зависимости от tвремении y координаты(рис. 09.1.4) бегущих плоских электромагнитных волнв (2.69) из раздела 2.0 "Колебания и волны" положительную сторону OY оси имеют следующий вид: EZ+ = (E0/2)cos(ωt - ky+ φ1) ↔ EZ+ = (E0/2)cos(ωt - ky); (4.1) HX+ = (H0/2)cos(ωt - ky+ φ2) ↔ HX+ = (H0/2)cos(ωt - ky),(4.2)
где φ1 = φ2 = 0 - начальные фазыколебанийвекторовнапряжённостейсоответственно
EZ+ электрическогополя вдоль OZ оси и HX+магнитногополя вдоль OX осибегущих плоских электромагнитных волн; ω -циклическая частотаколебаний векторов напряжённостей
EZ+ электрическогополя вдоль OZ оси и HX+магнитногополя вдоль OX осибегущих плоских электромагнитных волн; k = ω/c (2.70) из раздела 2.0 "Колебания и волны"- волновое число бегущих плоских электромагнитных волн; с - фазовая(9.10) из раздела 9.0 "Электромагнитные волны. Излучение" скорость плоской бегущей электромагнитной волны в вакууме, которая равна с скорости света в вакууме; E0/2 и H0/2 - амплитуды колебаний бегущих плоских электромагнитных волнв положительную сторону OY оси векторов напряжённостейсоответственно EZ+ электрического вдоль OZ оси и HX+магнитного вдоль OX оси полей.
|
соответственнонапряжённостей EZ электрическоговдоль OZ оси и HX магнитноговдоль OX оси полейимеет следующий вид: S+ = [EZ+, HX+ ] = [EZ+k, HX+i] = EZHXj, (4.3) где j - орт (1.1) из раздела 1.0 "Физические основы механики" в прямоугольной декартовой системе координат, направленный по OY оси и составляющий с k, i ортами, направленными соответственно по OZ, OX осям, правовинтовуюсистему, т.е. j = [k, i].
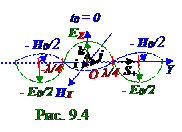
Согласно (4.3) вектор S+Пойнтинганаправлен (рис. 9.4) в положительную сторону OY оси и указывает направление переноса энергии(4.1), (4.2) плоской электромагнитной волной в эту положительную сторону OY оси.
Проекции EZ-, HX- на OZ, OX оси координат (9.24) из раздела 9.0 "Электромагнитные волны. Излучение" векторов соответственно напряжённостей EZ- электрического вдоль OZ оси и
HX-магнитного вдоль OX оси полей, в зависимости от tвремении y координаты(рис. 09.1.5) бегущих плоских электромагнитных волнв (2.72) из раздела 2.0 "Колебания и волны" отрицательную сторону OY оси имеют по аналогии с (4.1), (4.2) следующий вид:
EZ- = (E0/2)cos(ωt + ky+ φ1) ↔ EZ -= (E0/2)cos(ωt + ky); (4.4) HX- = - (H0/2)cos(ωt + ky+ φ2) ↔ HX- = - (H0/2)cos(ωt + ky), (4.5) где знак "-"перед проекцией HX- на OX ось вектора напряжённости HX- магнитноговдоль OX оси поля определяет ориентацию вектора S- Пойнтинга вотрицательную сторону OY оси.
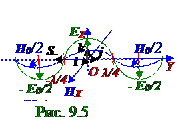
На рис. 9.5 изображена примерная графическая зависимость векторов напряжённостей EZ- электрическоговдоль OZ оси и HX- магнитноговдоль OX оси полей плоской электромагнитной волны, бегущейв отрицательную сторону OY оси, от y координатыв момент, t0 = 0 времени.
Вектор S- Пойнтинга(9.39) из раздела 9.0 "Электромагнитные волны. Излучение" с учётом (4.4), (4.5) направления (рис. 09.1.5) векторов напряжённостей EZ- электрическоговдоль OZ оси и HX- магнитноговдоль OX оси полейимеет следующий вид: S- = [EZ-, HX- ] = [EZ-k, -HX-i] = -EZ-HX-j, (4.6) где j - орт (1.1) из раздела 1.0 "Физические основы механики" в прямоугольной декартовой системе координат, направленный по OY оси и составляющий с k, i ортами, направленными соответственно по OZ, OX осям, правовинтовуюсистему, т.е. j = [k, i].
|
|
|
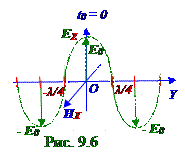
электромагнитных волнв (4.1), (4.2) положительную (рис. 9.4) ив (4.4), (4.5) отрицательную (рис. 9.5) стороны OY оси приводит к (рис.9.6) отсутствию в момент t0 = 0 времени вектора напряжённости HX магнитногополя вдоль OX осиплоской стоячей электромагнитной волны.
Дата добавления: 2016-02-14; просмотров: 1170;
