Намагниченность вещества, находящегося во внешнем магнитном поле

Если несущие ток проводники находятся в какой-либо среде, магнитное поле изменяется. Это объясняется тем, что всякое вещество является магнетиком, т.е. способно под действием магнитного поляприобретать магнитный момент или намагничиваться. Намагниченноевещество создаёт магнитное поле свектором B' индукции, которое накладывается на обусловленное токами в проводниках магнитное поле свектором B₀ индукции. Оба магнитных поля дают в сумме следующий результирующий вектор B индукции магнитного поля: B = B₀ + B'.(7.103) Под действием вектора B₀ индукции внешнего магнитного полявекторы p_m магнитных моментов молекул приобретают преимущественную ориентацию в одном направлении, вследствие чего магнетик намагничивается, т.е. его собственный суммарный векторB' индукции магнитного поля становится отличным от нуля. Вектор J намагниченностив ΔV малом объёме, взятый в окрестности рассматриваемой точки, равен сумме векторов p_m магнитных моментовотдельных молекул, поделённых на этот ΔV малый объём, вследствие чего для вектора J намагниченности имеет место следующее выражение: J = ∑p_m/ΔV, (7.104) ΔV

т.е. вектор J намагниченности магнетикаравен сумме векторов p_m магнитных моментовотдельных молекул, находящихся в единице объёма этого магнетика.

Связь молекулярных токов в магнетике с намагниченностью в интегральном виде

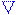
Ротор(7.30) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях" результирующего вектора B индукции магнитного поля в произвольной точке пространства с учётом (7. 103) имеет следующий вид: [ B ] = [B₀] + [ B']. (7.105) Согласно(7.30) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях" [ B₀ ] = μ₀jротор вектора B₀ индукции внешнего магнитного поля в произвольной точке пространства, занятого магнетиком, пропорционален вектору j плотности макроскопическогоили тока проводимости в этой точке пространства. Аналогично (7.30) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях" [ B']ротор собственного суммарного вектораB' индукции магнитного поля в произвольной точке пространства, занятого магнетиком, пропорционален вектору j_мол плотности молекулярныхтоков в этой точке пространства, вследствие чего [ B']ротор собственного суммарного вектораB' магнитной индукции поля имеет следующий вид: [ B'] = μ₀j_мол.(7.106) Подставляем (7.30) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях" (7.106) в (7.105) и получаем, что [ B] ротор

результирующего вектора B индукции магнитного поля в произвольной точке пространства, занятого магнетиком,пропорционаленсуммевекторов плотностей j макроскопического и

j_мол молекулярноготоков, вследствие чего [ B] ротор(7.105) результирующего вектора B индукции магнитного поля в произвольной точке пространства, занятого магнетиком, имеет следующий вид:

[B ] = μ₀(j + j_мол). (7.107) На рис. 7.25 изображена область магнетика, а в материале этого магнетика проведён воображаемыйГ контур, ограничивающий поверхность S площадью в магнетике в OXY плоскости.

Молекулярныетоки I_i_молсилой каждой молекулы текут по окружностямв OYZ плоскости, изображённым на рис.7.18 синими окружностями. Эти молекулярныетоки I_i_молсилой создают магнитные p_imмолекулярные моменты, которые в отсутствие вектора B₀индукции внешнего магнитного поля направлены хаотично, а при его наличии либо имеют направление, совпадающее с направлением вектора B₀ индукции внешнего магнитного поля, - это парамагнетики, либо имеют направление, противоположноес направлением вектора B₀ индукции внешнего магнитного поля, - это диамагнетики.Результирующий молекулярныйток I_молсилой ток через поверхность

S площадью, ограниченной воображаемымГ контуром, создают те молекулярныетоки I_i_молсилой, которые пересекают эту поверхность S площадью. Места пересечений магнетика молекулярнымитоками I_i_молсилой площадью отмечены на рис.7. 18 красными овалами.Молекулярный результирующийток I_молсилой в магнетикеток через поверхность S площадью, ограниченной воображаемымГ контуром, будут создавать лишь темолекулярные токи I_i_молсилой, траекториидвижения которых по окружности

оказываются "нанизанными"навоображаемыйГ контур. На рис.7.18 эти молекулярныетоки обозначенытоком I_i_мол'силой. Молекулярные токи I_i_мол'' силой, которые пересекают в магнетикеповерхность S площадью, ограниченной воображаемымГ контуром, дважды, т.е. один раз снизу и один раз сверху, не будут вносить вклад врезультирующий молекулярныйток I_молсилой, т.к. алгебраическаясумма таких токов при пересечении поверхности S площадью, будет равна нулю.

Результирующий молекулярныйток I_молсилой в магнетикечерез поверхность S площадью, которую ограничивает воображаемыйГ контур, имеет следующий вид: I_мол = ∫j_молdS, (7.108) S

где S - площадь (рис.7.25) поверхности в магнетике, "натянутая" на воображаемыйГ контур.

В выражении (7.108) из результирующего молекулярноготока I_молсилой исключаются молекулярные токи I_i_мол'' силой, которые пересекают в магнетикеповерхность S площадью, "натянутой" на воображаемыйГ контур,дважды, вследствие попеременного одинаковогои противоположного направления единичногоn нормальноговектора к элементарным поверхностям

dS площадью, в пределах которой определяется молекулярныйток с вектором j_мол плотности. Поэтому молекулярные токи I_i_мол'' силой, текущие через поверхность S площадью, а не по воображаемомуГ контуру, в результирующий молекулярныйток I_молсилой вклада не вносят. Результирующий молекулярныйток I_молсилой через поверхность S площадью образуют молекулярные токи I_i_мол' силой,траекториидвижения которых по окружности оказываются

(рис.7. 25) "нанизанными"на воображаемыйГ контур.

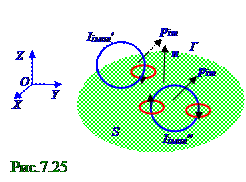
Перед(рис.7.26) и заплоскостью чертежа находится магнетик, верхняя и нижняя части которого разделены воображаемымГ контуром, находящимся в OYZ плоскости. Малаяdl часть воображаемогоГ контура является осью воображаемого косого цилиндра, изображенного на

рис.7.26 штрих - пунктирными красными линиями, основания которого перпендикулярны(7.104) вектору J намагниченностив магнетике, коллинеарного магнитным p_imмолекулярным моментам каждой молекулы и направленного впарамагнетике по вектору B₀индукции внешнего магнитного поля, либо вдиамагнетике противнаправления вектора B₀ индукции внешнего магнитного поля. Площадь основания воображаемого косого цилиндраравна S_молплощадикруга, по окружности которого текутмолекулярные токи I_i_мол' силой.

Все N молекул, которые обозначены на рис. 7.26 чёрными точками, попавшие в V объём воображаемого косого цилиндра, пересекаюттраекториямисвоихмолекулярных токов I_i_мол' силой в местах, отмеченных на рис. 7.26 красными овалами, поверхность магнетика в плоскости чертежа один раз ниже воображаемогоГ контура. Т.е. траекториидвижения этих токов I_i_мол' силой, изображённые на рис. 7.26 синими овалами, оказываются "нанизанными"на воображаемый

Г контур. Поэтому результирующий молекулярныйток I_молсилой на рис.7.19 в магнетике,

ограниченномвоображаемымГ контуром, будут создавать молекулярные токи I_i_мол' силой, траекториидвижения которых оказываются "нанизанными"на этот воображаемыйГ контур. Проекция S_мол┴ площади S_мол основания (рис. 7.26) воображаемого косого цилиндрана плоскость, перпендикулярную его dl оси имеет следующий вид: S_мол┴= S_молcosα, (7.109) где α - угол между вектором J намагниченностии dl осьювоображаемого,косого цилиндра, который равен, вследствие перпендикулярности вектора J намагниченностиплоскостям вращения молекулярных токов I_i_мол' силой, αуглумежду основанием воображаемого равновеликого прямого цилиндра и основанием воображаемого косого цилиндра.

Объём V (рис. 7.26) воображаемого косого цилиндраопределим с учётом равенства его объёмуравновеликого воображаемого прямого цилиндрас S_мол┴ площадьюоснования (7.109) и

dl длиной, вследствие чего V объём воображаемого косого цилиндра имеет следующий вид: V = S_мол┴dl = S_молdlcosα.(7.110)

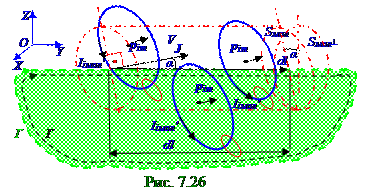
Количество N молекул, попавших в V объём (рис. 7.26) воображаемого косого цилиндра, с учётом их n концентрации и (7.78) значения этогоV объёма воображаемого косого цилиндра имеет следующий вид:N = nV = nS_молlcosα.(7.111)Суммарный I_мол_Vмолекулярныйток всех N молекул, попавших в V объём (рис. 7.26) воображаемого косого цилиндра, с учётом молекулярноготока I_i_мол'силой каждой из этих молекул, пересекающего V объём

воображаемого косого цилиндраодин раз, а также с учётом (7.110) имеет следующий вид: I_мол_V = I_i_мол'N = I_i_мол'nS_молdlcosα. (7.112) В (7.112) произведение I_i_мол'S_мол представляет собой (7.76) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях" модуль p_imвектора p_imмагнитного моментодной молекулы в магнетике, а произведение I_i_мол'nS_мол - модульвекторамагнитногомомента единицы объёма магнетика, т.е. согласно (7.45) - это модульJ вектора J намагниченности.

Поэтому с учётом равенства модуляJ вектора J намагниченности I_i_мол'nS_мол, т.е. J = I_i_мол'nS_мол, выражение (7.112) принимает следующий вид: I_мол_V = Jdlcosα, (7.113) где α - это (рис. 7.26) угол между вектором J намагниченности материаламагнетика ималымdl элементом воображаемогоГ контура, находящимся в OYZ плоскости и разделяющим верхнюю часть этого магнетика от нижней части.

Введя векторdl, направленный по (рис. 7.26) оси воображаемого косого цилиндра, преобразуем (7.113) в следующее скалярное произведение: I_мол_V = Jdl, (7.114) где I_мол_V - суммарныймолекулярныйток, пересекающий V объём косого цилиндра элементарной

dl длиной, или суммарныймолекулярныйток, "нанизанный"на элементарную dl длину воображаемогоГ контура.

Результирующий молекулярныйток I_молсилой в магнетике через поверхность S площадью (рис. 7.26), которую охватывает воображаемыйГ контур и включающий все малые dl элементы этого воображаемогоГ контура, с учётом (7.108) и (7.114) имеет следующий вид:

I_мол = ∫j_молdS = ∫Jdl, (7.115) S Г

где (7.115) является выражением, связывающим молекулярные токи в магнетике с намагниченностью в интегральном виде.

Связь молекулярных токов в магнетике с намагниченностью в дифференциальном виде

Перейдя в(7.115) с использованием теоремы Стоксаотинтегралапо Г контуру кповерхностномуинтегралу по поверхности S площадью, "натянутой" на этот Г контур, получим следующее выражение: ∫j_молdS = ∫Jdl= ∫[J]dS↔ j_мол = [ J].(7.116) S Г S

где (7.116) является выражением, связывающим молекулярные токи в магнетике с намагниченностью в дифференциальном виде.

Вектор j_мол плотности молекулярных токов определяется значением ротора [J]вектораJ намагниченности в магнетике. По аналогии с (5.42) из раздела 5.1 «Электрическое поле системы неподвижных зарядов в вакууме. Теорема Гаусса для электростатического поля. Работа и потенциал электростатического поля» ротор J вектора, т.е. rotJ намагниченности в магнетике для случая представления векторного поля в прямоугольной декартовой системе (1.1) из раздела 1.0 "Физические основы механики" координат определяется следующим выражением: i j k

j_мол= [ J] = rotJ = ∂/∂x ∂/∂y ∂/∂z = [(∂J_z /∂y) - (∂J_y /∂z)]i + [(∂J_x/∂z) - (∂J_z/∂x)]j + J_x J_y J_z

+ [(∂J_y /∂x) - (∂J_x /∂y)]k. (7.117) В случае, когда в произвольной точке пространства, занятого магнетиком, rotJ = 0, то в этой произвольной точке пространства плоскости вращения S_мол молекулярных I_i_мол токов единичных молекул ориентированы так, что вектор j_молрезультирующей плотности молекулярных токов в произвольной точке пространства равна нулю.

В произвольных точках пространства, занятого магнетиком, где rotJ ≠0, оказывается отличной от нуляи вектор j_молплотности молекулярных токов тоже отличен от нуля, причём векторы rotJ и j_мол плотности молекулярных токов имеют одинаковое направление.

Вектор напряженности магнитного поля и его связь с векторами индукции и намагниченности

Подставим (7.116) выражение связи вектора j_молплотности молекулярных токов с ротором

[J]вектораJ намагниченности в (7.107) выражение связи ротора [ B] результирующего вектора B индукции магнитного поля в произвольной точке пространства, занятого магнетиком, с суммойвекторов плотностей j макроскопического и j_мол молекулярноготоков, после чего получим следующее выражение связи ротора [ B/μ₀]этогорезультирующего вектора B индукции магнитного поля в произвольной точке пространства, занятого магнетиком, с вектором j плотностимакроскопического тока: [B ] = μ₀(j + j_мол)= μ₀j + μ₀[ J] ↔ [ , B/μ₀]=j + [ J]. (7.118) Объединим в (7.118) роторыи получим следующее выражение связи вектора j плотностимакроскопического тока в произвольной точке пространства, занятого магнетиком, с векторами B индукции магнитного поля и J намагниченности в этой произвольной точке пространства: [ ,[(B/μ₀) -J]] =j, (7.119) где j- вектор плотности макроскопическогоили тока проводимости в произвольной точке пространства.

Введём следующее выражение вектора H напряжённостимагнитного поля в произвольной точке пространства, занятого магнетиком, в (7.119) соотношение: (B/μ₀) -J = H. (7.120) Подставим (7.120) в (7.119) и получим следующее выражение связи вектора j плотностимакроскопического тока в произвольной точке пространства свектором H напряжённостимагнитного поля в этой произвольной точке, занятого магнетиком:

[ ,[(B/μ₀) -J]] = [ ,H] = rotH = [ H]= j.(7.121)

Теорема о циркуляции вектора напряжённости магнитного поля в дифференциальном и интегральном видах

Согласно (7.121) ротор вектора H напряжённостимагнитного поля впроизвольной точке пространства, занятого магнетиком, равен вектору j плотности макроскопическогоили тока проводимостив этой точке пространства.

Выражение (7.121) является теоремой о циркуляции вектора H напряжённостимагнитного поля по Г контуру, занятого магнетиком, в дифференциальном виде.

Возьмём в области пространства, занятого магнетиком, в котором существует вектор

H напряжённостимагнитного поля и вектор j плотности макроскопического или тока проводимости,произвольный воображаемыйГ контур с "натянутой" на него поверхностью S площадьюи образуем следующее выражение с использованием (7.121):

∫[H]dS= ∫jdS. (7.122) S S Перейдя в(7.122) с использованием теоремы Стоксаотинтеграла по поверхности S площадью, "натянутой" на воображаемыйГ контур, к интегралупо этому воображаемомуГ контуру, с учётом (7.28) из раздела 7.1 "Магнитостатика" результирующеготока I_рез силойв магнетике через поверхность S площадью, охватываемую этим воображаемымГ контуром, а также с учётом вектора j плотности макроскопическогоили тока проводимости через элементарную поверхность dS площадью этой поверхности S площадью, получим следующее выражение: ∫ [H]dS= ∫ Hdl= ∫ j dS = I_рез. (7.123) S Г S Согласно (7.123) циркуляция вектора H напряжённостимагнитного поля повоображаемомуГ контурув области пространства, занятого магнетиком, равнарезультирующему

I_рез макроскопическому или току проводимости через поверхность S площадью, которую охватывает этот воображаемыйГ контур.

Если макроскопические токи I₁, I₂ … I_n силой или токи проводимости текут по n проводам, охватываемымвоображаемымГ контуром, то (7.123) приобретает следующий вид: n

∫ Hdl = ∑I_i. (7.124) Г i = 1 Выражение (7.124) является теоремой о циркуляции вектора H напряжённостимагнитного поля повоображаемомуГ контурув области пространства, занятого магнетиком, в интегральномвиде: циркуляциявектора H напряжённостимагнитного поля повоображаемомуГ контуру, который охватывает в области пространства, занятого магнетиком, n проводников с токами I₁, I₂ … I_n силой, равняется алгебраическойсумме этих токов.

Магнитная восприимчивость и магнитная проницаемость. Диамагнетики, парамагнетики и ферромагнетики

В вакууме вектор J намагниченности J = 0, поэтомувектор H напряжённостимагнитного поля связан в вакуумесогласно (7.120) с вектором B₀индукции магнитного поля следующим образом: H = B₀/μ₀. (7.125) Вектор J намагниченностив области пространства, занятого магнетиком, принято связывать не срезультирующим вектором B индукции магнитного поля в произвольной точке пространства, занятого магнетиком, а свектором H напряжённостимагнитного поля в этой области пространства. С учётом (7.120) коллинеарности вектора B индукции магнитного поля и вектора H напряжённостиэтого магнитного поля векторJ намагниченности и вектор H напряжённостимагнитного поля области пространства, занятого магнетиком, связаны друг с другомследующим

χ коэффициентом пропорциональности : J = χH, (7.126) где χ - магнитная восприимчивостьматериала магнетика, которая у диамагнетиков отрицательна и мала по абсолютной величине, у парамагнетиковтоже невелика, но положительна, у ферромагнетиковположительна и достигает очень больших значений.

В изотропныхвеществах векторJ =χH намагниченности из(7. 126) совпадает по направлениюс вектором H напряжённости магнитного поля у парамагнетиков, т.к. магнитная

χвосприимчивостьэтих парамагнетиков положительна, а у диамагнетиковвектор

J намагниченности противоположенпо направлениювектору H напряжённостимагнитного поля, т.к.магнитнаяχвосприимчивостьэтих магнетиков отрицательна и мала по абсолютной величине.

У ферромагнитныхматериалов, например, у железа, кобальта и их сплавов связь междувектором J намагниченностиэтих материалов и вектором H напряжённости магнитного поля представляет собой сложную нелинейную зависимость.

Подставим (7.126) в (7.120) и получим следующую связь вектора H напряжённостимагнитного поля с результирующим вектором B индукции магнитного поля в произвольной точке пространства, занятого магнетиком: (B/μ₀- χH)= H ↔ H = B/μ₀(1 + χ)= B/μ₀μ, (7.127) где μ = (1+χ) - магнитная проницаемость, которая для однородных магнетиковявляется постоянной безразмерной величиной, а для неоднородных магнетиковзависитот координат точки пространства, в которой эта μ магнитная проницаемостьопределяется.

Согласно(7.127) вектор H напряжённости магнитного поляесть вектор, имеющий то же направление, что и результирующий вектор B индукции магнитного поля в произвольной точке пространства, занятого магнетиком, но в μ₀μ раз меньший по модулю.

Нормальные составляющие вектора напряжённости и индукции магнитного поля на границе раздела магнетиков

Согласно теореме (7.19) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях" Гауссав интегральной формеобщий Ф_mo магнитный поток через замкнутую поверхность S площадью равен нулю. На рис.7.27 замкнутая поверхность S площадью представляет собой в среде магнетиков воображаемый полуцилиндрс S₁площадями оснований, прямоугольного сечения в горизонтальной OYZ плоскости и цилиндрической боковой поверхностью S_бок площадью.Результирующие векторы B₁ и B₂ магнитной индукции поляв среде магнетиков с магнитными проницаемостямисоответственно μ₁ и μ₂ имеют нормальные составляющие B₁_n и B₂_nк верхней и нижней поверхностям воображаемого полуцилиндрас S₁ площадями оснований.

Вследствие противоположного направления вектора B₁ и положительной n₁нормали к верхней поверхности S₁ площадью, а также вследствие совпадениянаправления вектора B₂ и положительной n₂нормали к нижней поверхности S₁ площадью, проекции B₁_n иB₂_n на соответственно n₁, n₂нормалирезультирующих векторов B₁ и B₂ магнитной индукции поляв среде магнетиков смагнитными проницаемостями μ₁ и μ₂ имеют противоположные знаки.

С учётом (рис.7.27) малостиS_бок площади цилиндрической боковой поверхности по сравнению с S₁ площадями оснований воображаемого полуцилиндра общий Ф_mo магнитный поток через замкнутую поверхность S площадью этого воображаемого полуцилиндрав среде магнетиков будет состоять толькоиз нормальных составляющих B₁_n и B₂_nк верхней и нижней поверхностям S₁ площадьювоображаемого полуцилиндра.

С учётом теоремы (7.19) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях" Гауссав интегральной форме, противоположности знаков упроекций B₁_n иB₂_n на соответственно n₁, n₂нормалирезультирующих векторов B₁ и B₂ магнитной индукции поляв среде магнетиков с магнитными проницаемостямиμ₁ и μ₂, а также с учётом равенства верхнего и нижнего оснований S₁ площадьювоображаемых полуцилиндров общий Ф_mo магнитный поток через замкнутую поверхность S площадью этого воображаемого полуцилиндрав среде магнетиковимеет следующий вид: Ф_mo = B₂_n S₁- B₁_n S₁= 0 ↔ B₁_n = B₂_n. (7.128)

При определении в(7.128) общего Ф_mo магнитного потока через замкнутую поверхность (S) площадьювоображаемого полуцилиндране учитывались тангенциальные B_1τи B_2τ составляющиерезультирующих векторов B₁ и B₂ магнитной индукции поляв среде магнетиков с магнитными проницаемостямисоответственно μ₁ и μ₂, т.к. предполагалась малая h толщинавоображаемого полуцилиндрас S₁ площадямиоснований, вследствие чего: h → 0; S₂ → 0; S_бок → 0.

Поэтому магнитный потокчерез прямоугольное сечение S₂ площадьюи цилиндрическую боковую поверхностью S_бок площадью воображаемого полуцилиндра тоже стремитсяк нулю.

Подставим (7.127) B = μ₀ μH пропорциональной связи вектора H напряжённости магнитного полясрезультирующим вектором B магнитной индукции поляв среде магнетика с

μмагнитной проницаемостью,котороесправедливо, в частности, для проекций H₁_n, H₂_n на соответственно n₁, n₂нормали к верхней и нижней поверхности S₁ площади векторов H₁,H₂ напряжённостей магнитного поля, в выражение (7.128) и получим следующее соотношение между этими проекциями H₁_n, H₂_n на границе раздела магнетика с магнитными проницаемостямисоответственно μ₁ и μ₂:

μ₀ μ₁H₁_n = μ₀ μ₂H₂_n ↔ H₁_n/H₂_n = μ₂/μ₁. (7.129)

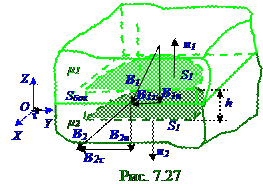
Таким образом, из (7.128) и (7.129)векторы нормальных составляющих B₁_n и B₂_n индукции магнитного поля на границе магнетиковсμ₁ и μ₂магнитными проницаемостямисохраняют своё направлениеи модуль, а векторы нормальных составляющих H₁_n и H₂_n напряжённости H магнитного поля сохраняют своё направление, но изменяютвеличинусвоего модуляпропорционально μ₂/ μ₁отношению магнитных проницаемостей μ₂ и μ₁.

Для случая μ₂> μ₁ векторы(рис. 7.27) нормальных составляющих H₁_n и H₂_n напряжённости

H магнитного поля сохраняют своё направление, но модуль(7.97)H₁_n больше H₂_n в μ₂/μ₁ раз.

Тангенциальные составляющие вектора напряжённости и индукции магнитного поля на границе раздела магнетиков

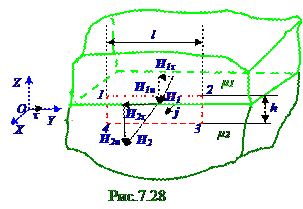
В (рис.7. 28) пренебрежении h толщиной 1 - 2 - 3 -4 контура, т.к. h → 0 циркуляция(7.124) вектора H напряжённостимагнитного поля поэтому1 - 2 - 3 -4 контуру в области пространства на границе магнетиковсμ₁ и μ₂магнитными проницаемостямиприналичии в общем случае вектора j плотности макроскопическихили токов проводимостина поверхностиграницы раздела магнетиков будет иметь следующий вид: ∫ Hdl = ∫H_1τdl + ∫H_2τdl = jl, (7.130) 1-2 -3-4 1-2 3-4

где j -модуль вектора j плотности тока, перпендикулярного ограниченной 1 - 2 - 3 -4 контуром поверхности, макроскопических или токов проводимостина границе раздела магнетиков; l - длина границы раздела магнетиков, по которой протекают токи проводимости.

Циркуляция (7.130) векторов H_1τиH_2τтангенциальныхсоставляющих вектора H напряжённостимагнитного поля при обходе 1 - 2 - 3 -4 контурапо "часовой стрелке" c учётом отрицательной проекции вектораdlна направление вектора H_1τ тангенциальнойсоставляющей вектора H напряжённостимагнитного поля приобходе 1 - 2 части контура l длиной, а также с учётом положительной проекции вектораdlна направление вектора H_2τ тангенциальнойсоставляющей вектора H напряжённостимагнитного поля приобходе3 -4 части контура l длиной имеет следующий вид: ∫Hdl = ∫H_1τdl + ∫H_2τdl= H_2τl - H_1τl = jl ↔ H_2τ - H_1τ = j. (7.131) 1-2 -3-4 1-2 3-4

Таким образом согласно (7.131) выражениювекторы H_1τиH_2τ тангенциальныхсоставляющихнапряжённости H магнитного поля на границе разделамагнетиковсмагнитными проницаемостямисоответственно μ₁ и μ₂приусловии наличия вектора j плотности макроскопических или токов проводимостина этой поверхностигранице раздела магнетиков сохраняют своё направление, но (рис.7.28) изменяютвеличинусвоего модуляна величину j модуля вектора j плотности тока проводимости, существующего на поверхностигранице раздела магнетикови перпендикулярного OYZ плоскости, в которой находятся векторы H напряжённостимагнитного поля.

При отсутствиивектора j плотности макроскопических или токов проводимостина поверхностиграницы раздела магнетиков(7.131) выражение принимает следующий вид:

H_2τ - H_1τ = 0 ↔ H_2τ = H_1τ. (7.132) Подставим (7.127) H = B/μ₀μ пропорциональной связи вектора H напряжённости магнитного полясрезультирующим вектором B магнитной индукции поляв среде магнетика с

μмагнитной проницаемостью,котороесправедливо, в частности, для проекций H_1τ, H_2τ на направление τ единичного (рис. 7.28) вектора векторов H₁,H₂ напряжённостей магнитного поля, в выражение (7.100) и получим следующее соотношение между проекциями B_1τ, B_2τна направление

τ единичного вектора результирующего вектора B индукции магнитного поля на границе раздела магнетика с магнитными проницаемостямисоответственно μ₁ и μ₂ при условии отсутствиявектора j плотности макроскопических или токов проводимостина этой поверхностигранице раздела магнетиков:B_1τ/μ₀ μ₁ = B_2τ/μ₀ μ₂↔ B_1τ/B_2τ = μ₁/μ₂.(7.133) Таким образом из (7.132), (7.133)векторы H_1τ и H_2τ тангенциальныхсоставляющих вектора H напряжённости магнитного поля на границе магнетиковсмагнитными проницаемостямисоответственно μ₁ и μ₂сохраняют своё направлениеи модуль, а векторы тангенциальныхсоставляющихвектора B индукции магнитного поля B_1τ и B_2τ сохраняют своё направление, но изменяютвеличинусвоего модуляпропорциональноотношению магнитных проницаемостей μ₁ и μ₂при условии отсутствиявектора j плотности макроскопических или токов проводимостина этой поверхностиграницы раздела магнетиков.

Для случая μ₂> μ₁ векторы(рис. 7.27) тангенциальныхсоставляющихвектора B индукции магнитного поля B_1τ и B_2τ сохраняют своё направление, но модуль(7.133)B_2τ больше B_1τ в μ₂/μ₁ раз.

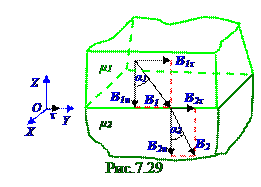
Векторы B индукции (рис.7.29) магнитного поля B₁, B₂ в среде магнетиков с μ₁ и μ₂магнитными проницаемостямисоответственно имеют согласно (7.128)равные нормальные составляющие B₁_n и B₂_n.Тангенциальныесоставляющиевектора B индукции магнитного поля B_1τ, B_2τ зависят при отсутствиивектора j плотности макроскопических или токов проводимостина поверхностигранице раздела магнетиков согласно (7.133) от величин μ₁ и μ₂магнитных проницаемостей. Поэтому α₁угол c учётом (7.128), (7.133)между нормальной

Дата добавления: 2016-02-14; просмотров: 1370;