ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ. Изучение процесса осаждения
Изучение процесса осаждения
Твердых частиц в жидкости
В химической технологии часто возникает необходимость разделения неоднородных смесей на составляющие фазы. Примерами таких неоднородных смесей являются пыли - взвеси частиц твердого вещества в газе; туманы - взвеси мелких капель жидкости в газе; эмульсии - взвеси капель жидкости в другой жидкости несмешивающейся с первой; суспензии - взвеси частиц твердого вещества в жидкости.
Разделение таких неоднородных смесей путем осаждения может быть осуществлено несколькими способами:
- путем гравитационного осаждения, т.е. под действием сил тяжести;
- под действием центробежных сил;
- под действием сил электрического притяжения в электрическом поле.
Гравитационное осаждение является простейшим методом разделения неоднородных смесей. На практике его осуществляют в аппаратах, называемых отстойниками. Для расчета последних необходимо знать скорость осаждения частиц.
Если плотность шарообразной частицы ρч диаметром dв процессе гравитационного осаждения больше плотности жидкости ρЖ, то твердая частица будет осаждаться в жидкости, в противном случае, если ρч < ρж, частица будет всплывать (рисунок 1).
Кроме изменения направления движения частицы, принципиального различия между этими способами нет.
Если частица осаждается в жидкости под действием сил тяжести и начальная скорость ее движения равна нулю,
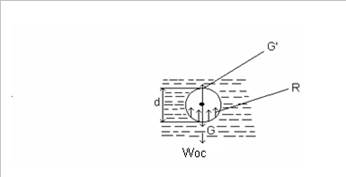
Рисунок 1 -
то частица будет двигаться вначале ускоренно, и баланс сил будет выражаться уравнением
DWос
G - G’- R = m---------- (1)
dτ
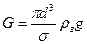
где G - сила тяжести, равная весу частицы, Н;
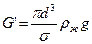
G/ - подъемная сила, равная весу вытесненной жидкости, H;
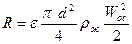
R - сила сопротивления жидкости, отнесенная к поперечному
сечению частицы, H;
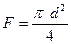 |
где e- коэффициент сопротивления, безразмерный;
Wос - скорость осаждения, м/с;
t- время, с;
m- масса частицы, кг;
Правая часть уравнения (1) представляет собой силу инерции. Однако под влиянием силы сопротивления R ускоренное движение частицы сменится замедленным, а начиная с некоторого момента времени, частица будет осаждаться с постоянной скоростью. В условиях постоянной скорости осаждения баланс сил будет иным:
G - G’- R = 0, (2)
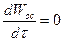 |
так как
Поскольку при постоянной скорости осаждения время движения частиц с ускорением мало по сравнению с общей длительностью процесса осаждения, то с достаточной для технических расчетов точностью можно период движения частицы с ускорением исключить из дальнейшего рассмотрения.
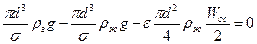 |
Уравнение (2) в развернутом виде запишется:
|
откуда скорость осаждения
|
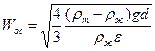 |
Уравнение (4) включает коэффициент сопротивления 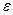 , который зависит от режима осаждения. В связи с этим необходимо рассмотреть гидравлические режимы осаждения.
, который зависит от режима осаждения. В связи с этим необходимо рассмотреть гидравлические режимы осаждения.
Исследования показывают, что наблюдаются три режима осаждения: ламинарный, переходный и турбулентный. В пределах каждого режима характер обтекания частицы жидкостью специфичен (рисунок 2). При ламинарном режиме осаждения жидкость обтекает частицу без образования вихрей (рисунок 2а).
При турбулентном режиме осаждения за частицей образуется цепочка вихрей, т.н. вихревая дорожка (рисунок 2в). Переходный режим (рисунок 2 б) является промежуточным между ламинарным и турбулентным.
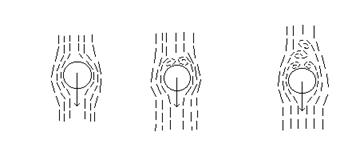 |
а б в
Рисунок 2 – Различные режимы движения частицы
Изменение характера обтекания при переходе одного режима к другому как раз обусловливает изменение характера зависимости коэффициента.
Область существования режимов осаждения (аналогично режимам движения жидкости в трубопроводах) определяется величиной критерия Рейнольдса
Re = Wос *dэкв *rж/mж,(5)
при Re £ 1,85наблюдается ламинарный режим осаждения;
при 1,85 £ Re £ 500–переходный режим;
при Re > 500 – турбулентный режим.
Коэффициент сопротивления e также зависит от Re.
Причем в ламинарном режиме
e = 24/Re, (6)
в переходном
e = 18,5/Re0,6, (7)
в турбулентном
e = 0,44. (8)
Постановка значений из уравнений (6 - 8) в уравнение (4) невозможна, т.к. неизвестен режим движения. Целесообразно поэтому переходить к критериальным уравнениям.
Решив уравнение (4) относительно e, получим
|
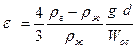 |
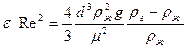 |
Умножив левую и правую часть на Re2, после сокращения приходим к выражению
|
Дробь в правой части уравнения (10) представляет собой безразмерный комплекс, носящий название критерия Архимеда
|
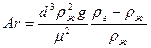 |

|
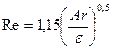 |
Тогда уравнение (10), решенное относительно Re, запишется:
В общем случае осаждающиеся частицы не шарообразны, а форма частиц должна при расчете скорости осаждения учитываться. С этой целью в уравнение (12) вводится коэффициент формы ψ,
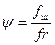 |
представляющий собой отношение поверхности частицы шарообразной формы ƒш к поверхности частицы данной формы ƒг, но того же веса. Для частиц шарообразной формы коэффициент формы равен 1, поскольку ƒш = ƒг, а для частиц любой иной формы ψ< 1, поскольку ƒш < ƒг. С учетом коэффициента формы уравнение (12) имеет вид
|
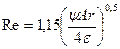 |
Совместное решение уравнения (13) с уравнениями (6 - 8) дает расчетные критериальные уравнения для расчета скорости осаждения:
в ламинарном режиме, при
Re < 1,85 или при ψ*Ar < 33
|
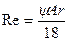 |
в переходном, при 1,85 < Re< 500 или при 33 < ψ*Ar< 82500
Re = 0,152*(ψ*Ar)0,715 ; (15)
в турбулентном, при Re> 500 или при ψ*Ar> 82500
Re = 1,74*(ψ*Ar)0,75. (16)
Критериальные зависимости (13 - 16) могут быть представлены в общем виде:
Re = m Arn(17)
Откуда
LgRe = lgm + n*lgAr. (18)
|
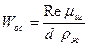 |
Удобство уравнений (13 - 17) заключается в том, что искомая величина входит только в критерий Рейнольдса, а величины, входящие в критерий Архимеда, известны по условиям задачи. Известен также коэффициент формы ψ. Поэтому по величине произведения ψ*Ar можно судить о режиме осаждения и для определения Re, а следовательно и Woc, воспользоваться необходимым уравнением. При найденном численном значении Reскорость осаждения определяется как
|
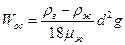 |
В практике осаждения наиболее распространен ламинарный режим осаждения. Раскрывая для этого случая уравнение (13) и решая его относительно Woc (принимая ψ= 1), получим
Уравнение (20) позволяет проанализировать влияние параметров на Woc в ламинарном режиме, что предлагается сделать студентам самостоятельно.
В приведенных выше формулах размерности первичных единиц следующие: размерность длины - м, размерность времени - с, размерность массы - кг (система СИ).
Обратим внимание на физический смысл критериев подобия Рейнольдса и Архимеда.
Критерий Рейнольдса является мерой отношения инерционных сил в жидкостном покое (в данном слое при обтекании частицы) и вязкостных сил. При малых значениях Re поток жидкости формируется в условиях преобладания вязкостных сил над силами инерции и при обтекании частицы не происходит образование вихрей (рисунок 2). При больших значениях Re, наоборот, преобладает действие инерционных сил. Возникшие при обтекании частицы возмущения жидкостного потока вязкостные силы погасить не могут, и за частицей возникает цепочка вихрей (рисунок 2в).
Критерий Архимеда является мерой отношения подъемной силы (разности сил веса и Архимедовой силы) к вязкостным силам.
Таким образом, критериальные уравнения (13 - 17) в специфической форме учитывают не только действующие на частицу в процессе осаждения силы (2), но и характерные особенности обтекания частицы жидкостью.
На рисунке 3 приведен логарифмический график зависимости критерия Рейнольса от критерия Архимеда для различных режимов осаждения частиц согласно уравнению (18).
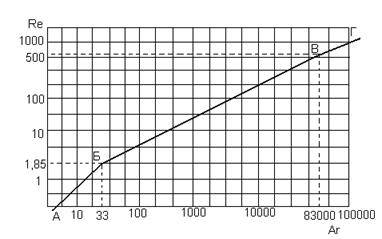 |
Рисунок 3 - Зависимость критерия Рейнольса от критерия Архимеда для различных режимов осаждения частиц
ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ
Установка состоит из трех стеклянных цилиндров, заполненных глицерином с концентрацией 50, 70 и 100%, а, следовательно, и различной вязкостью. Вверху и внизу каждого цилиндра нанесены метки, фиксирующие расстояние, которое частицы проходят в процессе осаждения. Замеряя время, в течение которого частицы проходят расстояние между метками (1 м), можно определить скорость осаждения частицы. С целью исключить влияние ускоренного участка движения частицы в жидкости верхняя метка на 30 - 40 мм ниже уровня жидкости.
| <== предыдущая лекция | | | следующая лекция ==> |
| ВОЗМОЖНОСТИ ИХ ВОЗНИКНОВЕНИЯ В РАЙОНАХ СТИХИЙНЫХ БЕДСТВИЙ И КАТАСТРОФ. | | | Единицы измерения ионизирующих излучений. |
Дата добавления: 2016-03-15; просмотров: 1456;
