Проводники второго рода, явления, связанные с перемещением ионов

Растворы электролитов – это проводники второго рода. В них электрический ток обусловлен перемещением заряженных частиц (ионов) под действием приложенной разности потенциалов. В таких системах наблюдаются два типа явлений:

1. Явления, связанные только лишь с перемещением ионов (заряженных частиц) в растворе;

2. Явления, где изменяется механизм переноса электричества, так, называемые электродные процессы.

Сейчас будет рассмотрена первая группа явлений, а электродные процессы будут рассмотрены в разделе «электрохимия».

Способность растворов электролитов проводить электрический ток называется электропроводностью (L). Электропроводность – это величина, обратная сопротивлению проводника электрического тока R:

L = 1/ R , [L]= ом^-1

Сопротивление проводника электрического тока R пропорционально длине проводника и обратно пропорционально площади поперечного сечения проводника: _l

ρ - удельное сопротивление, т.е. сопротивление проводника с длиной l =1 м и площадью сечения S =1 м² (как видно, объем такого проводника 1 м³). Таким образом, единицы измерения [ρ]= Ом_*м.

Величина, обратная удельному сопротивлению называется удельной электропроводностью (χ - «капа»):

χ = 1/ρ ,т.е. [χ]= Ом^-1_*м^-1

Очевидно, что электропроводность раствора зависит от концентрации ионов, но зависимость эта сложная: с увеличением концентрации ионов увеличивается количество носителей заряда, но с другой стороны, усиливается электростатическое взаимодействие, снижающее скорость их движения, а следовательно, и их способность проводить электрический ток, поэтому на графике (см. рис.χ =f(С)) представлена экстремальная зависимость, проходящая через maximum.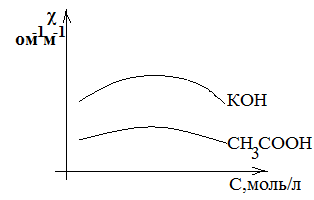

Кроме этого, удельная электропроводность зависит и от скорости движения ионов, которая обусловлена:

1. Разной природой ионов (их размером, зарядом, степенью гидратации);

2. Разной природой растворителя (его диэлектрической проницаемостью, вязкостью);

3. Различными внешними условиями (например, температурой). Известно, что повышение температуры раствора на 1^оС увеличивает величину удельной электропроводности на 2 – 2,5 % вследствие уменьшения вязкости раствора.

Для устранения двойственного (экстремального) влияния концентрации электролита на электропроводность его раствора, вводят понятие эквивалентной электропроводности (λ -«лямбда»), т. е. электропроводности раствора, приведенной к единичной его концентрации.

Эквивалентная электропроводность раствора – это электропроводность раствора, содержащего один эквивалент электролита в 1 м³ раствора, и поэтому для каждого конкретного раствора, может быть легко определена по формуле:

λ _v = 1000 χ / С_N ;[λ] = ом^-1_*м²_*экв^-1

λ _v– эквивалентная электропроводность при данной концентрации раствора,

С_N – нормальная концентрация раствора.

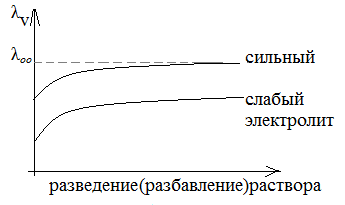
С уменьшением концентрации раствора (с увеличением разведения раствора) (см. рис.λ_v= f(разведение)) эквивалентная электропроводность достигает предельного значения при бесконечном разведении раствора (λ _оо).

Таким образом, эквивалентная электропроводность при бесконечном разведении (λ_∞) зависит только от скорости движения ионов.

Закон Кольрауша.

Было установлено, что при бесконечном разведении катионы и анионы электролитов движутся и, следовательно, проводят электрический ток независимо друг от друга: λ _оо = λ _к + λ _а

Это утверждение носит название закон Кольрауша.В этом законе величиныλ _к и λ _а имеют смысловое значение подвижностей катиона и аниона, соответственно. Они измеряются экспериментально в единицах эквивалентной электропроводности:

λ _к = F _* U_k ; λ _а = F _* U_a

F - число Фарадея (96480 кулонов)

U_k и U_a - абсолютные скорости движения катиона и аниона, соответственно.