Простейшие геометрические фигуры

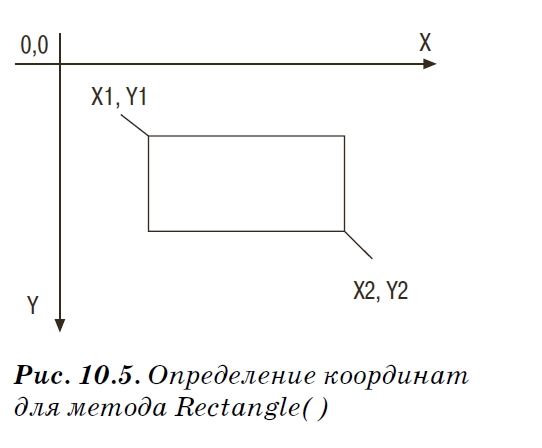
Для рисования прямоугольника можно

воспользоваться методом Rectangle(). Процедура является перегружаемой и в качестве параметров принимает координаты верхнего левого (X1, Y1) и нижнего правого (X2, Y2) углов прямоугольника или координаты, заданные в формате TRect (рис. 10.5):

procedureRectangle(X1, Y1, X2, Y2:

Integer); overload;

procedureRectangle(constRect:

TRect); overload;

Прямоугольник со скругленными углами получится при использовании метода:

procedureRoundRect(X1, Y1, X2, Y2, X3, Y3: Integer);

Первые четыре параметра соответствуют координатам вершин функции Rectangle(). Значения X3 и Y3 определяют степень сглаживания углов, задавая ширину и высоту скругляющего эллипса (рис. 10.6).

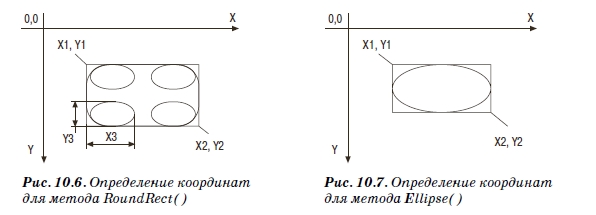
Вы уже заметили, что большинство методов GDI рисуют простейшие геометрические фигуры внутри ограничивающей прямоугольной области. Например, эллипс (рис. 10.7) вписывается в рамки прямоугольника с координатами, аналогичными процедуре Rectangle():

procedureEllipse(X1, Y1, X2, Y2: Integer); overload;

procedureEllipse(constRect: TRect); overload;

Следующие три родственных метода посвящены прорисовке части эллипса:

procedureArc(X1, Y1, X2, Y2, X3, Y3, X4, Y4 : Integer);

procedureChord(X1, Y1, X2, Y2, X3, Y3, X4, Y4: Integer);

procedurePie(X1, Y1, X2, Y2, X3, Y3, X4, Y4 : Longint);

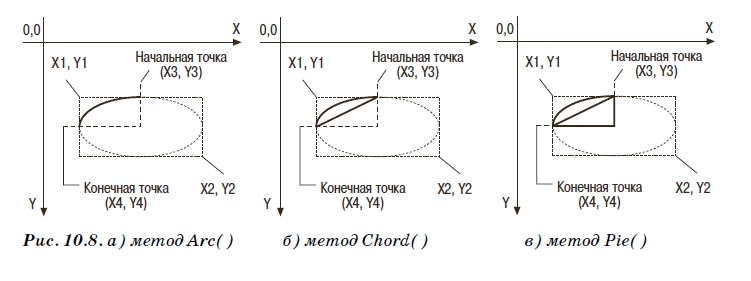
Процедура Arc() чертит сегмент, Chord() – хорду, а Pie() – сектор эллипса (рис. 10.8). Как вы уже догадались, все изображения вписываются в эллипс (а точнее в прямоугольник, содержащий эллипс) с координатами вершин (X1, Y1) и (X2, Y2). Логические координаты (X3, Y3) и (X4, Y4) описывают воображаемые лучи, исходящие из центра эллипса. Места пересечения лучей с контуром эллипса соединяются дугой. Начальной точкой дуги считается пересечение эллипса с лучом (X3, Y3), конечной – с лучом (X4, Y4).

Для рисования сегмента окружности (рис. 10.9) пользователи Windows NT могут воспользоваться функцией Windows API AngleArc() (к сожалению, эта функция не поддерживается в Windows 95/98/Me):

functionAngleArc(HDC: hdc; X,Y: integer; dwRadius: Longword; eStartAngle, eSweepAngle : real):boolean;

В качестве параметров функции AngleArc() выступают: HDC – дескриптор контекста устройства; X и Y – координаты центра окружности; dwRadius – радиус окружности в пик селах; eStartAngle – угол (в градусах) относительно оси Х, определяющий начальную точку сектора; eSweepAngle – угол раскрытия сектора.

Методы Rectangle(), Ellipse(), RoundRect(),

Chord() и Pie() предназначены не только

для рисования простейших геометрических фигур, но и для закрашивания текущей кистью ограниченной этими фигурами области. По умолчанию кисть сплошная и белая.