Геометрические и кинематические параметры
Лекция 7
Краткое содержание.
Общие сведения. Геометрические и кинематические параметры. Червячные передачи со смещением. Скольжение в червячной передаче и КПД. Расчет прочности зубьев. Материалы и допускаемые напряжения. Тепловой расчет.
Червячные передачи
Общие сведения
Червячная передача – это механизм для передачи вращения зацеплением с непосредственным контактом витков червяка и зубьев червячного колеса (рис.1).
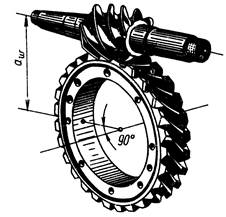
Рис.1
Червяк – это винт с трапециидальной или близкой к ней по форме резьбой. Червячное колесо является косозубым зубчатым колесом с зубьями особой дуговой формы. Такая форма зубьев обеспечивает увеличение длины и прочности зубьев на изгиб.
Червячные передачи применяют при необходимости передачи движения между перекрещивающимися валами. Угол перекрещивания обычно равен 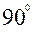 .
.
Достоинства червячных передач: 1) возможность получения большого передаточного числа в одной ступени; 2) плавность и малошумность в работе; 3) повышенная кинематическая точность; 4) возможность обеспечения самоторможения.
Недостатки червячных передач: 1) низкий КПД; 2) необходимость изготовления зубьев колеса из дорогих антифрикционных материалов; 3) повышенные требования к точ6ности сборки, необходимость регулировки; 4) необходимость специальных мер по интенсификации теплоотвода. Указанные недостатки ограничивают мощность червячных передач (обычно до 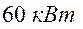 ).
).
Червячные передачи применяют в станках, автомобилях, подъемно - транспортных машинах и других машинах.
Геометрические и кинематические параметры
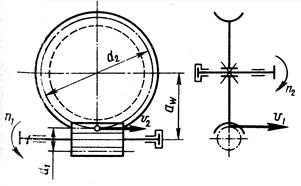
В червячной передаче различают диаметры начальных и делительных цилиндров (рис.2): 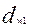 ,
, 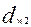 – начальные диаметры червяка и колеса;
– начальные диаметры червяка и колеса; 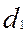 ,
, 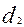 – делительные диаметры червяка и колеса. В передачах без смещения
– делительные диаметры червяка и колеса. В передачах без смещения 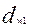 =
= 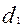 ,
, 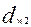 =
= 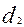 .
.
 | |||
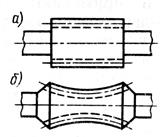 | |||
Рис.2 Рис.3
По форме тела червяки разделяют на цилиндрические (рис 3, а) и глобоидные ( рис. 3, б). По форме профиля резьбы – с прямолинейным (рис 4, а) и криволинейным (рис. 4 ,б) в осевом сечении. Наиболее распространены цилиндрические червяки. Цилиндрические червяки бывают видов: архимедов червяк, теоретический торцовый профиль которого – архимедова спираль; эвольвентный червяк, теоретический торцовый профиль которого – эвольвента. Архимедов червяк можно нарезать на обычных токарных или резьбофрезерных станках. Поэтому их широко применяют. С целью повышения работоспособности стали применять шлифованные высокотвердые червяки. Для шлифования архимедовых червяков требуются специальные шлифовальные круги фасонного профиля. Поэтому архимедовы червяки изготовляют в основном с нешлифованными витками при 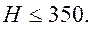
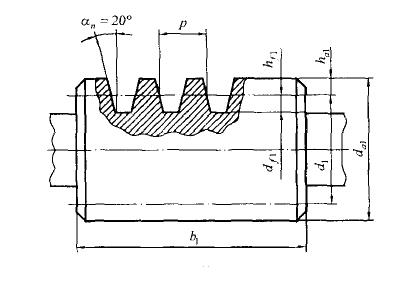
Рис.4 Геометрические параметры червяка
В червячных передачах угол профиля 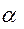 принимают равным
принимают равным 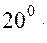 . Расстояние между одноименными точками боковых сторон смежных витков червяка называют шагом
. Расстояние между одноименными точками боковых сторон смежных витков червяка называют шагом 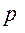 червяка. . Отношение
червяка. . Отношение 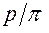 называют осевым модулем
называют осевым модулем 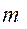 . Резьба червяка может быть однозаходной или многозаходной. Число заходов червяка обозначают
. Резьба червяка может быть однозаходной или многозаходной. Число заходов червяка обозначают 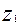 . По стандарту,
. По стандарту, 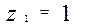 ;
; 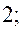
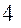 . Рекомендуют:
. Рекомендуют: 
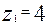 при передаточном отношении
при передаточном отношении 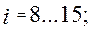
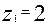 при
при 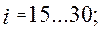
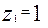 при
при 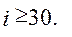
Делительный диаметр червяка принимается кратным модулю:
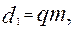 (1)
(1)
где 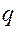 – коэффициент диаметра червяка. Значения
– коэффициент диаметра червяка. Значения 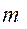 и
и 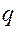 стандартизованы. Ряд модулей, мм: 1,0; 1,25; 1,6; 2,0; 2,5; 3,15; 4,0; 5,0; 6,3; 8,0 и т.д. Ряд
стандартизованы. Ряд модулей, мм: 1,0; 1,25; 1,6; 2,0; 2,5; 3,15; 4,0; 5,0; 6,3; 8,0 и т.д. Ряд 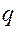 : 8; 10; 12,5; 16; 20; 25. Рекомендуют
: 8; 10; 12,5; 16; 20; 25. Рекомендуют 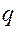 >
> 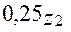 .
.
Угол подъема витка червяка на делительном диаметре
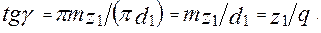 (2)
(2)
Диаметры вершин и впадин:
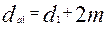 ;
; 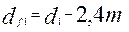 . (3)
. (3)
Длина 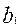 нарезанной части червяка:
нарезанной части червяка:
при числе витков 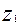 =
= 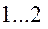

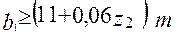 ;
;
при числе витков 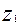 =
= 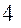
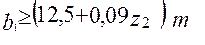 .
.
Примечание. Для шлифуемых и фрезеруемых червяков полученную величину b1 следует увеличить на 25 мм – при m < 10 мм; на 35…40 мм – при m = 10…16 мм.
Червячные колеса. Минимальное число зубьев червячных колес в силовых передачах 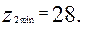 Наиболее желательно для силовых передач
Наиболее желательно для силовых передач 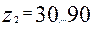 . Геометрические параметры червячного колеса, нарезанного без смешения (рис. 5), равны:
. Геометрические параметры червячного колеса, нарезанного без смешения (рис. 5), равны:
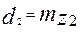 ;
; 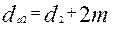 ;
; 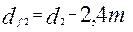 ;
;
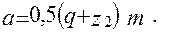 (4)
(4)
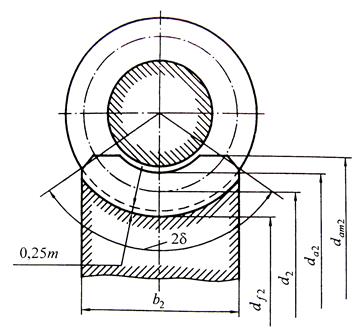
Рис. 5 Геометрические параметры червячного колеса
Ширина колеса 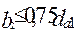 (при
(при 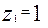 или
или 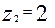 ),
), 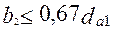 (при
(при 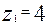 ).
).
Наибольший диаметр колеса можно определить по формуле
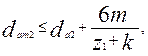 (5)
(5)
где 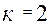 для архимедовых и эвольвентных червяков.
для архимедовых и эвольвентных червяков.
Дата добавления: 2016-03-05; просмотров: 1407;
