Геометрические вероятности.
Пусть множество между множеством 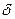 , которое является бесконечным бессчётным множеством и все исходы которого предполагаются равновозможными и пусть между точками этого множества и точками некоторого множества сигма-прямой, плоскости ил пространства, имеющего длину, площадь или объём, установлено взаимооднозначное соответствие, а также, в результате этого соответствия, каждому событию А. Взаимнооднозначно соответствует помножество сигма и имеющее меру: длина, площадь или объём.
, которое является бесконечным бессчётным множеством и все исходы которого предполагаются равновозможными и пусть между точками этого множества и точками некоторого множества сигма-прямой, плоскости ил пространства, имеющего длину, площадь или объём, установлено взаимооднозначное соответствие, а также, в результате этого соответствия, каждому событию А. Взаимнооднозначно соответствует помножество сигма и имеющее меру: длина, площадь или объём.
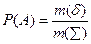 (1)
(1)
Вероятность по формуле 1.ю называется геометрической вероятностью события.
Формула 1 часто записывается в виде, с учётом того, что пространство исходов отождествлено с множеством омега.
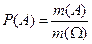 (2)
(2)
Пример. На окружности единичного радиуса случайным образом появляются 3 точки: A, B и С. Найти вероятность того, что треугольник ABC – остроугольный.
Решение.
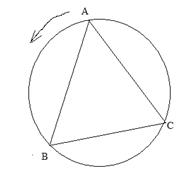
Будем измерять длины дуг единичной окружности между точками в таком направлении, чтобы при движении по окружности за точкой А, следовала точка B, а затем C.
Обозначим:
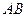 x
x
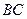 y
y
Тогда различным 3-м точкам на окружности, мы на координатной плоскости Oxy поствим точки с координатами x,y 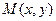 .
.
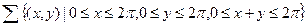
 ,
, 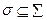
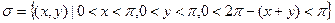
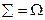
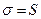
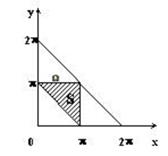
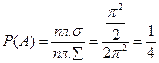
Пример. Два человека обедают в столовой, которая открыта с 12 часов до 13 часов. Каждый из них приходит в произвольный момент времени и обедает в течение 10 минут. Какова вероятность их встречи?
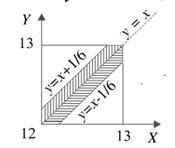
Пусть x – время прихода первого лица в столовую, y – время прихода второго, таким образом, исходы ситуации можно описать парами чисел: 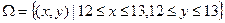 .
.
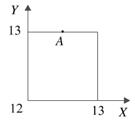
Пусть А – событие, состоящее в том, что встреча состоялась.
Первый случай.
Пусть 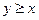 , то есть первый пришёл не позже второго. Каким условием мы характеризуем, что встреча состоялась?
, то есть первый пришёл не позже второго. Каким условием мы характеризуем, что встреча состоялась? 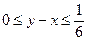 .
.
Второй случай.
Пусть 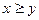 , то есть второй пришёл не позже первого.
, то есть второй пришёл не позже первого. 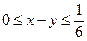
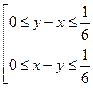
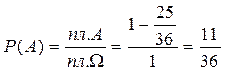
Дата добавления: 2016-04-11; просмотров: 5017;
