Вычисление координат вершин теодолитного хода

Невязки в приращениях координат замкнутого полигона (рис. 12.8, а). Известно, что сумма проекций замкнутого поли­гона на любую координатную ось равна нулю, следовательно, теоретически алгебраическая сумма приращений координат дол­жна быть

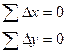(12.17)

Но так как результаты измерений углов и линий содержат ошибки, вследствие которых практически

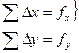(12.18)

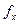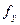величины и называются невязками в приращениях коорди­нат соответственно по оси абсцисс и по оси ординат.

Прежде чем распределять эти невязки, надо убедиться в их допустимости, для чего необходимо вычислить невязку в пери­метре

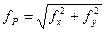(12.19)

и определить ее допустимость по формуле

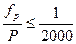, (12.20)

где Р — периметр полигона.

Если невязка в периметре допустима, то невязк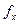и и 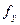рас­пределяют с обратным знаком соответственно на все прираще­ния 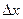и 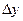пропорционально длинам линий с округлением до 0,01 м.

Контролем вычисления поправок служит равенство: сумма поправок в приращениях по оси абсцисс и оси ординат должна равняться невязке с обратным знаком. Полученные поправки алгебраически прибавляют к соответствующим приращениям и получают исправленные приращения. Сумма исправленных при­ращений по каждой оси в замкнутом полигоне должна равняться нулю.

После исправления приращений вычисляют координаты всех вершин полигона, пользуясь правилом: координата последующей точки равна координате предыдущей точки плюс соответствую­щее приращение. Для вычисления этих координат надо иметь исходные координаты, которые получают путем привязки теодо­литного хода к опорной геодезической сети либо выбирают про­извольно.

Контролем вычисления координат является последовательное вычисление координат точек замкнутого полигона, чтобы в ре­зультате получить координаты исходной точки.

Невязки в приращениях разомкнутого хода (см. рис. 12.1,6) определяются по формулам

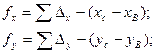(12.21)

Координаты начального и конечного пунктов хода известны. Невязка 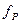в периметре вычисляется по формуле (12.19), а ее допустимость по формуле (12.20). Если ход проложен между пунктами теодолитного хода (см. рис. 12.8, б), то допустимость невязки определяется по формуле

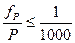(12.22)

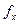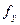Распределение невязок и , вычисление исправленных при­ращений и координат пунктов разомкнутого хода выполняются так же, как и в замкнутом полигоне.

Контролем служит сумма исправленных приращений по оси абсцисс и оси ординат, равная разности соответствующих ко­ординат конечной и начальной точек хода. Последовательно вычисляя координаты хода по исходным координатам началь­ного пункта, получаем координаты конечного пункта.

Обработку угловых измерений, вычисление дирекционных углов и румбов, вычисление приращений и координат вершин теодолитного хода выполняют в специальной ведомости, кото­рую принято называть ведомостью координат.

Пример вычисления координат замкнутого теодолитного хода приведен в табл. 12.2. В графу 2 ведомости вычисления коорди­нат выписываются из журнала полевых измерений (табл. 12.1) средние значения горизонтальных углов хода, а в графу 6 сред­ние значения длин линий, измеренных в прямом и обратном направлениях. При углах наклона, превышающих 1°, в длины линий вводится поправка за наклон. По формуле (12.2) находится угловая невязка, которая в приведенном примере 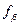= —1,2', т. е. меньше предельной невязки 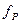=2,4', вычислен­ной по формуле (12.3). Следовательно, угловая невязка допу­стима, она распределяется с обратным знаком поровну на все измеренные углы.

Исправленные углы записываются в графу 3. Сумма исправ­ленных углов в замкнутом полигоне равна теоретической сумме, в приведенном примере равна 720°.

По исходному дирекционному углу линии 1—2, равному 10°40' (графа 4), вычисляются дирекционные углы всех осталь­ных сторон по формулам (12.5), т. е.

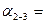10°40' + 180° — 118°03,2' = 72°36,8'; 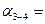72°36,8' + 180⁰ —103°32,2' = 149⁰4,6'; ….

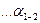= 291°50,7' + 180° —101°10,7'—360°= 10°40' (!) Последняя строка контрольная.

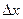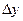По дирекционным углам вычисляются румбы и записыва­ются в графу 5 ведомости. По горизонтальным проложениям линий (графа 6) и значениям румбов вычисляются с помощью микроЭВМ типа «Электроника» или таблиц приращения коор­динат и по формулам (12.12) и записываются в графы 7 и 8. Суммируя приращения по осям X и У, получают по фор­муле (12.18) невязки 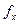= —0,37 и 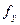= +0,05.

Относительная невязка в периметре, вычисленная по фор­муле (12.20), равна 1/3400, т. е. меньше предельно допустимой - 1/2000. Следо­вательно, невязк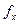и и 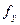допустимы, они распределяются с об­ратным знаком на приращения пропорционально длинам линий по формулам

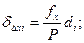
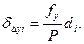
Сумма поправок должна равняться невязкам с обратным зна­ком. Поправки округляются до сантиметров. В графы 9 и 10 ведомости записываются значения исправленных приращений. Сумма исправленных приращений в замкнутом полигоне должна равняться нулю. После проверки этого условия вычисля­ются координаты. По исходным координатам первой точки x = + 500,00 и y = +500,00 вычисляются координаты всех ос­тальных точек замкнутого теодолитного хода, т. е.

X₂ = +500,00 + 329,60 = +829,60; y₂ = +500,00+ 62,04 = +562,04;

X₃ = +829,60 + 53,18= +882,78; y₃ = +562,04 + 169,66 =+731,70;

………………………………………………………………………….

X₁ =+450,80+49,20 =+ 500,00; y₁ = + 622,63—122,63 = +500,00 (!).

Последняя строка является контрольной. Если вычисление ко­ординат проводится в произвольной системе, то целесообразно координаты исходной точки взять такими, чтобы все координаты были положительными.

Пример обработки диагонального хода приведен в табл.12.3.

При обработке диагонального хода теоретическая сумма измеренных углов вычисляется по формуле (12.8). Для данного примера (см. рис. 12.8, б)

,

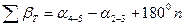где 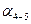и 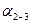взяты из ведомости координат основного хода (см. табл. 12.2), т. е.

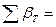205°42,4'—72°36,8' +180°*4= 853°05,6'. Исключив из этой суммы 360°, получают

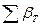= 493°05,6^/.

Таблица 12.2