Журнал измерения горизонтальных углов и линий
| №№ стан- ций | №№ точек визир. | Отсчеты по горизонтальному кругу | Угол из полу приемов | Среднее значение угла | Длина линий, м. | Угол наклона линии | Примечание | ||||
| Основной полигон | |||||||||||
| 12 | |||||||||||
| 2610 | 11,5/ 01,0 36,0 25,0 | 1010 | 10,0| 11,0 | 1010 | 10,5| | 335,23 | +00 | 20| | Оптический теодолит 2Т30, точность отсчета 0,5/ | ||
| 26,5 24,0 04,5 01,0 | 02,5 03,5 | 03,0 | 335,35 177,81 | +00 | 34| | ||||||
| 2460 | 47,0/ 15,0 38,0 06,0 | 1030 | 32,0| 32,0 | 1030 | 32,0| | 177,77 257,31 | -00 | 37| | |||
| 1790 | 03,0/ 41,0 54,0 32,0 | 230 | 22,0| 22,0 | 1230 | 22,0| | 257,26 185,84 | -00 | 23| | |||
| 1450 | 41,5/ 40,0 17,0 15% | 1310 | 01,5| 01,5 | 1310 | 01,5| | 185,80 166,76 | +20 | 30| | |||
| 2710 | 57,5/ 08,0 03,0 13,0 | 1420 | 40,5| 50,0 | 1420 | 49,8| | 166,72 132,14 | -00 | 17| | |||
| 132,10 Диагональный ход С точки 5 на точку 2 основного полигона | |||||||||||
| 780 | 24,0/ 14,0 20,5 10,0 | 750 | 10,0| 10,5 | 750 | 10,2| | 134,01 | +00 | 25| | |||
| 2140 | 50,5/ 08,0 44,0 01,0 | 1120 | 42,5| 43,0 | 1120 | 42,8| | 134,03 94,28 | +00 | 30| | |||
| 2690 | 59,5/ 04,0 29,0 34,0 | 2400 | 55,5| 55,0 | 2400 | 55,2| | 94,32 216,50 | -00 | 27| | |||
| 1180 | 34,0/ 18,0 06,5 50,0 | 640 | 16,0| 16,5 | 640 | 16,2| | 216,58 |
Для получения исходных координат и дирекционного угла теодолитного хода его нужно привязать к пунктам триангуляции или полигонометрии, координаты которых известны.
Если ход проходит через пункт А опорной сети (рис. 12.3, а), то привязка заключается в измерении примыкающих углов в этой точке для передачи дирекционного угла на линию теодолитного хода, например, 3—4.
Если теодолитный ход не проходит через пункт опорной сети, то в этом случае от одного из пунктов хода прокладывают наиболее короткий теодолитный ход до пункта опорной сети и измеряют в этом ходе углы и линии для передачи координат и дирекционного угла, например, на пункт 8 и дирекционного угла на линию 8—9 (рис. 12.3, б).
3. Съёмка ситуации местности
Для съемки ситуации применяются различные способы, изложенные ниже.
1. Способ перпендикуляров. Этот способ применяется при съемке ситуации и местных предметов, имеющих правильные геометрические формы, например, зданий, а также криволинейных контуров, например, рек, дорог и других вытянутых в длину контуров.
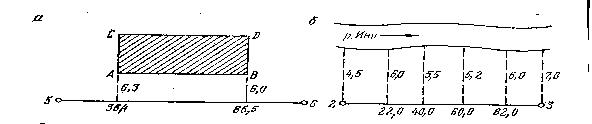
Рис. 12.4. Схемы съемки ситуации способом перпендикуляров
Перпендикуляры опускают из снимаемых точек здания или точек контура местности на стороны теодолитного хода. Например, положение точек. А и В (рис. 12.4, а) определится длиной перпендикуляров и расстоянием от точки 5 теодолитного хода до этих перпендикуляров. Положение точек С и D получают по данным обмера здания рулеткой.
На рис.12.4, б показана запись измерений при съемке берега реки способом перпендикуляров. Длина перпендикуляров допускается при съемке в масштабе 1:5000 — 10 м; 1:2000 — 8 м; 1:1000 — 6 м; 1:500 — 4 м. При такой длине перпендикуляры от снимаемых характерных точек опускаются на линию на глаз, более длинные — с помощьюэккера
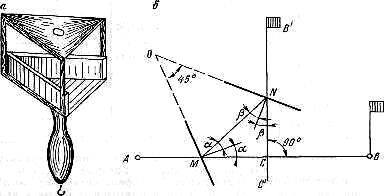
Рис. 12.5. Двух зеркальный эккер: а — внешний вид эккера; б — ход лучей в экере
Двухзеркальный эккер (рис. 12.5, а) — простейший прибор, у которого два зеркала установлены под углом 45°. Зеркала прикреплены с внутренней стороны к корпусу, имеющему ручку с крючком, на котором подвешивается отвес. Над зеркалами в корпусе вырезаны окошечки. Луч из точки В (рис. 12.5,б), падающий на зеркало М под углом 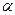 , отражается и падает на другое зеркало N под углом
, отражается и падает на другое зеркало N под углом 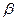 и, отразившись от этого зеркала, попадает в глаз наблюдателя по направлению СС'. Это направление пересекает линию АВ под углом 90°.
и, отразившись от этого зеркала, попадает в глаз наблюдателя по направлению СС'. Это направление пересекает линию АВ под углом 90°.
Чтобы восставить перпендикуляр в точке С к линии АВ, держат эккер по отвесу в данной точке С так, чтобы зеркало М было обращено к вехе В. Затем, смотря в другое зеркало N и в окошечко над ним, выставляют веху В' по направлению изображения вехи В в этом зеркале.
При опускании перпендикуляра из точки В' на АВ перемещаются с эккером по линии АВ до тех пор, пока изображение вехи В закроет веху В'.
Эккер исправен, если угол между зеркалами установлен правильно, т. е. 45°. Поверка этого условия выполняется так: к прямой АВ в точке С восставляют зккером перпендикуляр по обеим вехам А и В.
Если оба перпендикуляра сольются в одно направление, то эккер исправен. В противном случае, действуя исправительными винтами, изменяют положение зеркал, добиваются их совпадения.
При применении эккера длины перпендикуляров допускаются до 80 м при съемке в масштабе 1:5000, до 60 м при съемке в масштабе 1 :2000, до 40 м при съемке в масштабе 1 : 1000 и до 20 м при съемке в масштабе 1 :500.
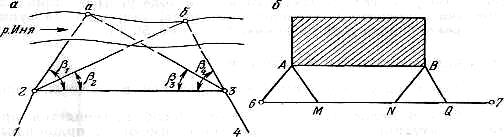
Рис.12.6. Способы съемки ситуации: а — угловых засечек;; б — линейных засечек
2.Способ угловых засечек. Этот способ выгодно применять при съемке труднодоступных контуров, например, при съемке противоположного берега реки. В этом случае при точках 2 и 3 (рис, 12.6, а) теодолитом измеряют одним полуприемом углы 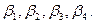 Засечки точек а и бдолжны быть под углом не менее 30° и не более 150°.
Засечки точек а и бдолжны быть под углом не менее 30° и не более 150°.
Построением на плане этих углов получим точки а и б на противоположном, относительно линии теодолитного хода, берегу реки.
3. Способ линейных засечек. Способ применяется при съемке зданий (рис.12.6,б).В этом случае положение точки А определяется измерением расстояний 6А, 6М и МА. Эти расстояния измеряются лентой или рулеткой, и они должны быть примерно равными. Для получения на плане точки А надо построить треугольник 6МА. Положение точки В определяется аналогично, но измеряются расстояния 6N, 6Q, NB и QB, причем NQ — часть стороны теодолитного хода 6—7. Построением на плане этих углов получим точки а и б на противоположном, относительно линии теодолитного хода, берегу реки.
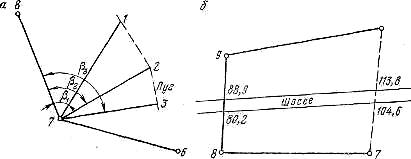
Рис, 12.7. Способы съемки ситуации: а — полярный; б — створов
4. Способ полярных координат или полярный способ. Суть полярного способа съемки ситуации заключается в том, что точки 1, 2, 3,... (рис.12.7, а) определяются в системе полярных координат, т. е. горизонтальными углами 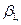 ,
, 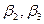 , образованными начальным направлением 7—8 и расстояниями 7—1, 7—2, 7—3 от точки полюса 7 до снимаемых точек. Эти расстояния определяются с помощью нитяного дальномера и не должны превышать при съемке масштаба 1:5000—150 м; 1:2000 — 100 м; 1:1000 — 60 м. Углы измеряются одним полуприемом. Чтобы не делать вычислений, поступают так: совмещают нулевой штрих алидады с нулевым штрихом лимба и, вращая лимб, визируют на точку 8. Для съемки точек 1, 2, 3 вращением алидады последовательно визируют на дальномерную рейку, устанавливаемую на эти точки, и записывают отсчеты по лимбу, равные углам
, образованными начальным направлением 7—8 и расстояниями 7—1, 7—2, 7—3 от точки полюса 7 до снимаемых точек. Эти расстояния определяются с помощью нитяного дальномера и не должны превышать при съемке масштаба 1:5000—150 м; 1:2000 — 100 м; 1:1000 — 60 м. Углы измеряются одним полуприемом. Чтобы не делать вычислений, поступают так: совмещают нулевой штрих алидады с нулевым штрихом лимба и, вращая лимб, визируют на точку 8. Для съемки точек 1, 2, 3 вращением алидады последовательно визируют на дальномерную рейку, устанавливаемую на эти точки, и записывают отсчеты по лимбу, равные углам 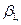 ,
, 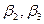 , и расстояния, взятые по дальномеру. Для контроля визируют вновь на точку 8 и делают отсчет, который не должен отличаться от нуля более 2'. Результаты измерений этим способом записывают в журнал.
, и расстояния, взятые по дальномеру. Для контроля визируют вновь на точку 8 и делают отсчет, который не должен отличаться от нуля более 2'. Результаты измерений этим способом записывают в журнал.
5. Способ створов. Этот способ применяется при съемке точек, расположенных в створе линии теодолитного хода, либо в створе линии, опирающейся на точки теодолитного хода (рис.12.7,б).
При съемке ситуации составляется абрис. Абрис является схематическим чертежом, на котором показывают все снимаемые точки с соблюдением порядка и взаимного расположения контуров местности между собой и относительно опорных линий. Абрис составляется отдельно для каждой стороны теодолитного хода и снятой ситуации с этой стороны. Абрис ведут карандашом четко и аккуратно с записями всех выполненных при съемке угловых и линейных измерений.
4. Обработка результатов полевых измерений
При теодолитной съемке получают геодезический журнал измерений углов, линий и абрис. Эти документы служат основным материалом для построения плана. Поэтому обработку результатов полевых измерений начинают
с проверки правильности всех записей и вычислений, сделанных в журнале, а также вычислений поправок за наклон сторон теодолитного хода. Дальнейшая обработка измерений при теодолитной съемке складывается из следующих действий: обработка угловых измерений и вычисление дирекционных углов и румбов сторон, вычисление приращений и координат вершин теодолитного хода, построение плана участка теодолитной съемки.
Угловая невязка замкнутого хода. Известно, что теоретическая сумма углов плоского многоугольника равна
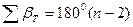 , (12.1)
, (12.1)
где 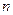 — число углов многоугольника.
— число углов многоугольника.
Пусть практическая сумма измеренных углов замкнутого многоугольника (рис. 12.8, а) равна 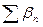 .
.
Разность между практической суммой измеренных углов и теоретической суммой называется угловой невязкой полигона и обозначается через 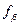 .
.
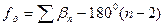 . (12.2)
. (12.2)
Для углов, измеренных теодолитом тридцатисекундной точности полным приемом, допустимая предельная невязка суммы углов определяется по формуле
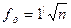 , (12.3)
, (12.3)
а для углов, измеренных теодолитом одноминутной точности,
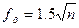 . (12.4)
. (12.4)
Допустимая невязка распределяется с обратным знаком поровну на все углы с округлением до 0,1|.
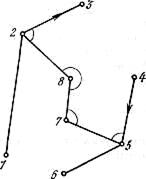

Рис. 12.8. Схемы обработки теодолитных ходов: а — замкнутого хода; б — диагонального хода
Сумма всех поправок в углы должна равняться невязке 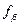 с обратным знаком, а сумма исправленных углов — удовлетворять формуле (12.1).
с обратным знаком, а сумма исправленных углов — удовлетворять формуле (12.1).
Вычисление дирекционных углов и румбов сторон замкнутого хода. Исходный дирекционный угол 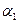 например, стороны 1—2 хода (рис. 10.7, а) получают в результате привязки этой стороны к пунктам геодезической опорной сети или определяют для нее истинный или магнитный азимут.
например, стороны 1—2 хода (рис. 10.7, а) получают в результате привязки этой стороны к пунктам геодезической опорной сети или определяют для нее истинный или магнитный азимут.
По известному дирекционному углу 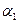 и по исправленным углам
и по исправленным углам 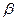 вычисляют дирекционные углы всех сторон замкнутого хода по формулам
вычисляют дирекционные углы всех сторон замкнутого хода по формулам
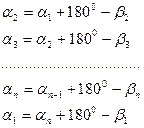 (12.5)
(12.5)
Последняя строка равенств (12.5) контрольная.
По дирекционным углам вычисляют румбы, пользуясь их зависимостью между собой.
Угловая невязка разомкнутого теодолитного хода. На рис. 12.2,б показан разомкнутый ход, проложенный между пунктами В и С опорной сети. Координаты исходных точек А, В и С, D опорной сети и дирекционные углы  и
и 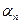 известны. Для определения дирекционных углов разомкнутого теодолитного хода напишем формулы
известны. Для определения дирекционных углов разомкнутого теодолитного хода напишем формулы
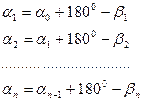 (12.6)
(12.6)
Сложив равенства (10.6), получим
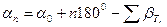 (12.7)
(12.7)
откуда
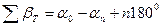 , (12.8)
, (12.8)
Угловая невязка
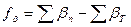 (12.9)
(12.9)
Допустимость угловой невязки 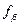 в разомкнутом ходе определяется по формуле (12.3) или (12.4). Распределение допустимой невязки, вычисление дирекционных углов и румбов сторон разомкнутого теодолитного хода выполняются так же, как и в замкнутом полигоне.
в разомкнутом ходе определяется по формуле (12.3) или (12.4). Распределение допустимой невязки, вычисление дирекционных углов и румбов сторон разомкнутого теодолитного хода выполняются так же, как и в замкнутом полигоне.
5. Прямая и обратная геодезические задачи
При вычислительной обработке результатов измерений на местности, при проектировании инженерных сооружений и перенесении их в натуру возникает необходимость решать прямую и обратную геодезические задачи.
Прямая геодезическая задача. Даны координаты 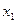 и
и 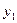 точки А начала линии АВ, ее горизонтальное проложение
точки А начала линии АВ, ее горизонтальное проложение 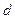 и дирекционный угол
и дирекционный угол 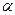 . Требуется определить координаты
. Требуется определить координаты 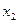 и
и 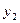 точки В конца этой линии (рис. 12.9) . Из рис. 12.9 видно, что координаты
точки В конца этой линии (рис. 12.9) . Из рис. 12.9 видно, что координаты
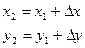 (12.10)
(12.10)
Разности координат конечной и начальной точек линии АВ, т. е. 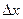 и
и 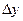 называются приращениями координат:
называются приращениями координат:
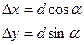 (12.11)
(12.11)
 При помощи румбов приращения координат вычисляются по popмулам:
При помощи румбов приращения координат вычисляются по popмулам:
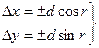 (12.12)
(12.12)
Приращения координат имеют знаки, которые зависят от знака косинуса и синуса дирекционного угла или от названия румба линии:
Румбы.......... СВ ЮВ ЮЗ СЗ
Приращения:
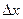 .......... + - -
.......... + - -
Рис. 12.9. Прямая и обратная 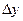 .......... + + - -
.......... + + - -
геодезические задачи
Вычисление приращений координат выполняют с помощью таблиц натуральных значений sin и cos или с помощью вычислительных машин.
Обратная геодезическая задача. Даны координаты х1 и у1 точки А начала линии АВ и координаты х2, у2 точки В конца этой линии. Требуется определить длину и дирекционный угол или румб этой линии. Из рис. 12.9 следует, что
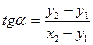 (12.13)
(12.13)
или
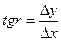 , (12.14)
, (12.14)
где- г определяют по таблицам натуральных значений тригонометрических функций или с помощью микрокалькулятора. Название румба определяют по знакам 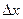 и
и 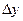 . Зная румб, можно вычислить дирекционный угол
. Зная румб, можно вычислить дирекционный угол 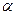 . Расстояние
. Расстояние 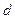 можно вычислить по формулам
можно вычислить по формулам
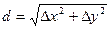 (12.15)
(12.15)
или
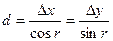 . (12.16)
. (12.16)
Дата добавления: 2016-03-15; просмотров: 4735;
