КРИТЕРИИ РАЗРУШЕНИЯ НА ОСНОВЕ ТЕОРИИ ТРЕЩИН
известно, что реальная прочность твердых тел во много раз меньше теоретической, равной 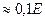 , где Е – модель Юнга. Объясняется это тем, что реальные тела имеют разного рода микро- и макродефекты: трещины, поры, узкие полости, инородные включения и т.п. Распределение этих дефектов в объеме тела, как правило, случайно, и поэтому случайна величина прочности материала. Экспериментально это убедительно подтверждается тем, что наблюдается разброс (иногда довольно значительный) при испытаниях одинаковых образцов в одинаковых условиях, и имеет место так называемый масштабный эффект: большие образцы имеют меньшую прочность чем малые образцы той же формы. Это характерно для всех хрупких тел вообще, горных пород и тампонажного камня в частности.
, где Е – модель Юнга. Объясняется это тем, что реальные тела имеют разного рода микро- и макродефекты: трещины, поры, узкие полости, инородные включения и т.п. Распределение этих дефектов в объеме тела, как правило, случайно, и поэтому случайна величина прочности материала. Экспериментально это убедительно подтверждается тем, что наблюдается разброс (иногда довольно значительный) при испытаниях одинаковых образцов в одинаковых условиях, и имеет место так называемый масштабный эффект: большие образцы имеют меньшую прочность чем малые образцы той же формы. Это характерно для всех хрупких тел вообще, горных пород и тампонажного камня в частности.
Кроме того, современные экспериментальные данные свидетельствуют о постепенном развитии разрушения и о большой роли первичных дефектов в формировании картины разрушения. Трещины начинаются развивается задолго до полного разрушения тела. Разрушение не единовременный акт, оно развивается с большей или меньшей скоростью при сравнительно невысоких напряжениях и представляет собой некоторый динамический процесс (см. разд. 4.2).
Поэтому прежние представления о наступлении разрушения при достижении некоторого критического напряжения материала устарели.
Для оценки реальной прочности тел необходимо исходить из наличия в теле дефектов. При этом важное значение приобретает использование современных результатов теории трещин [33]. Хотя эти результаты не позволяют охватить все многообразие особенностей разрушения, но их использование дает инженеру необходимый инструмент для более правильной оценки прочности тел и для более глубокого понимания причин разрушения. С помощью теории трещин можно количественно объяснить больше различие между реальной и теоретической прочностью тел, влияние масштабного фактора, различие между прочностью на сжатие и растяжение и многое другое.
Гриффитс впервые показал, что низкая реальная прочность хрупких тел вызывается наличием трещин, приводящих к значительной концентрации напряжений. В основе теории Гриффитса лежит представление об энергетическом барьере – поверхностной энергии, который необходимо преодолеть для развития трещины, т.е. для образования новой поверхности. В то же время при увеличении трещины освобождается потенциальная энергия, которая может быть израсходована на разрушение.
Любой материал в данных условиях (температура, влажность, внешняя среда и т.д.) характеризуется некоторой плотностью поверхностной энергии 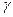 , которая определяет величину работы, необходимую для образования единицы новой свободной поверхности. Энергетический критерий Гриффитса формулируется следующим образом: разрушение тела развивается, если плотность освобождающейся энергии достигает критического значения. Например, для трещины длиной 2l в поле равномерно растяжения напряжением p в условиях плоской деформации (рис. 52) критерий Гриффитса записывается в виде
, которая определяет величину работы, необходимую для образования единицы новой свободной поверхности. Энергетический критерий Гриффитса формулируется следующим образом: разрушение тела развивается, если плотность освобождающейся энергии достигает критического значения. Например, для трещины длиной 2l в поле равномерно растяжения напряжением p в условиях плоской деформации (рис. 52) критерий Гриффитса записывается в виде
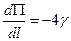 ,
,
где 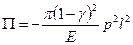 - потенциальная энергия тела.
- потенциальная энергия тела.
Отсюда следует условие предельного равновесия при растяжении
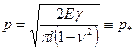 . (4.33)
. (4.33)
Если при данной длине трещины напряжение 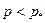 , то трещина не растет. Если же напряжение достигает критического значения
, то трещина не растет. Если же напряжение достигает критического значения 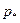 , то трещина расширяется. Из формулы (4.33) вытекает, что не предельное напряжение
, то трещина расширяется. Из формулы (4.33) вытекает, что не предельное напряжение 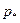 - прочностная характеристика материала, а произведение
- прочностная характеристика материала, а произведение
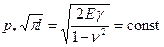 . (4.34)
. (4.34)
В инженерных расчетах используется более удобный силовой критерий прочности Ирвина, который по существу эквивалентен критерию Гриффитса, но основан на особенности распределения напряжений в окрестности вершины трещины:
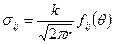 ,
,
где r, 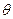 - локальная система координат с началом в вершине трещины, k – коэффициент интенсивности напряжений (КИН), который зависит от формы тела, системы нагрузок и геометрии трещины.
- локальная система координат с началом в вершине трещины, k – коэффициент интенсивности напряжений (КИН), который зависит от формы тела, системы нагрузок и геометрии трещины.
Согласно критерию Ирвина, для каждого материала есть критическое значение коэффициента интенсивности напряжений 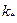 , по достижении которого трещина начинает расти, т.е. для прочности тела необходимо, чтобы
, по достижении которого трещина начинает расти, т.е. для прочности тела необходимо, чтобы
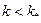 .
.
Таким образом, для оценки влияния трещин на прочность тела необходимо решить соответствующую задачу теории упругости, найти КИН и сравнить его с опытной для данного материала величиной 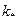 .
.
Напряжения и перемещения около вершины трещины для каждого типа раскрытия определяются коэффициентами интенсивности 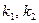 и
и 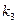 нормального напряжения, поперечного и продольного сдвигов соответственно. Иногда в литературе используют другие обозначения КИН
нормального напряжения, поперечного и продольного сдвигов соответственно. Иногда в литературе используют другие обозначения КИН 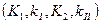 и вводят иные физические понятия. Например, согласно Г.И. Баренблатту,
и вводят иные физические понятия. Например, согласно Г.И. Баренблатту, 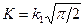 называют модулем сцепления, а
называют модулем сцепления, а 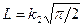 - сдвиговым модулем сцепления.
- сдвиговым модулем сцепления.
В простейших случаях равномерного растяжения плоскости (рис. 52) плоского и антиплоского сдвигов (рис. 54) коэффициенты интенсивности напряжений вычисляются по формулам
 ,
,
где 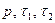 - соответственно силы растяжения, плоского и антиплоского сдвигов.
- соответственно силы растяжения, плоского и антиплоского сдвигов.
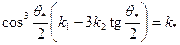 , (4.35)
, (4.35)
где 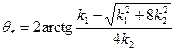 - угол начального распространения трещины относительно ее направления (ориентации).
- угол начального распространения трещины относительно ее направления (ориентации).
Отсюда и находятся критические значения внешней нагрузки, при которой начинается локальное разрушение тела. Например, при равномерном растяжении или сжатии плоскости с трещиной, расположенной под углом 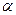 к направлению внешней силы, имеют место следующие формулы для определения:
к направлению внешней силы, имеют место следующие формулы для определения:
Коэффициентов интенсивности напряжений
 ;
;
угла начального распространения трещины
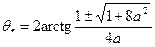 .
.
Предельного напряжения
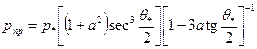 ,
,
где верхние знаки соответствуют растяжению, а нижние – сжатию; 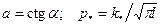 -критическое значение напряжения при растяжении плоскости с трещиной, перпендикулярной к направлению растяжения [см. рис. 52 и формулу (4.33)].
-критическое значение напряжения при растяжении плоскости с трещиной, перпендикулярной к направлению растяжения [см. рис. 52 и формулу (4.33)].
Коэффициенты интенсивности напряжений при указанных на рис. 57 видах нагружения вычисляются по формуле [7]
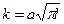 ,
,
где
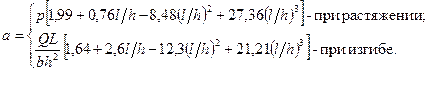
разрушение образца в целом определяется локальной прочностью его наиболее слабого элемента объема.
Функция распределения прочности 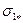 при хрупком разрушении представляется следующим образом:
при хрупком разрушении представляется следующим образом:
 (4.36)
(4.36)
где  - параметры закона распределения, подлежащие определению из опытов.
- параметры закона распределения, подлежащие определению из опытов.
Последнее выражение с помощью двукратного логарифмирования можно преобразить в уравнение прямой
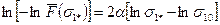
в координатах 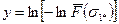 и
и 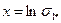 . Обычно для построения прямой
. Обычно для построения прямой 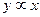 используются абсциссы
используются абсциссы 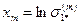 и соответствующие им ординаты
и соответствующие им ординаты 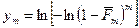 , где
, где 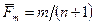 ; т – номер наблюдаемого значения прочности (расположены в порядке возрастания); п – общее число наблюдений.
; т – номер наблюдаемого значения прочности (расположены в порядке возрастания); п – общее число наблюдений.
Для определения параметров 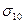 и
и 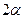 используется либо графическое построение, либо метод наименьших квадратов. В результате
используется либо графическое построение, либо метод наименьших квадратов. В результате
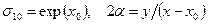 ,
,
где 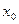 - значение х при у = 0.
- значение х при у = 0.
Доказано, что параметр 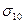 связан с объемом тела. Если найден параметр
связан с объемом тела. Если найден параметр  для образца объемом
для образца объемом 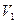 , то для образца объемом
, то для образца объемом 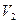 будет
будет 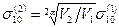 .
.
Вероятность разрушения образца под действием напряжения 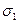 вычисляется по формуле
вычисляется по формуле
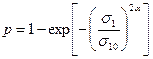 ,
,
где отношение 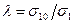 можно рассматривать как коэффициент безопасности.
можно рассматривать как коэффициент безопасности.
Отсюда легко доказать, что для двух образцов, объемы которых 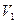 и
и 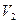 , разрушение равновероятно, если выполняется соотношение
, разрушение равновероятно, если выполняется соотношение
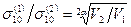 .
.
В общем случае результаты испытаний на прочность могут быть приближены одним уравнением (4.36) лишь в довольно ограниченном интервале. Чаще для адекватного описания требуются две прямые с различным наклоном. Точка пересечения этих прямых может означать изменение самого механизма разрушения.
Для того, чтобы определить влияние на хрупкое разрушение неоднородного поля напряжений, сравнивают наибольшее напряжение в неоднородном поле напряжений в момент разрушения с разрушающим напряжением в однородном поле, используя условие равной вероятности разрушения.
Например, в случае чистого изгиба балки имеет место следующее соотношение между прочностью на изгиб и прочностью на растяжение:
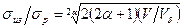 ,
,
где V – объем образца, испытываемого на растяжение; 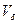 - объем балки. Если, например,
- объем балки. Если, например, 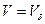 и
и 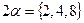 , то
, то 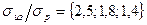 .
.
Статистический подход к хрупкому разрушению при трехмерном напряженном состоянии может быть основан на допущении, что по отношению к разрушению напряжения 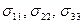 не взаимодействуют. Тогда сравнение с вероятностью разрушения под действием одноосного нагружения напряжением
не взаимодействуют. Тогда сравнение с вероятностью разрушения под действием одноосного нагружения напряжением  дает уравнение равной вероятности разрушения
дает уравнение равной вероятности разрушения
 ,
,
представляющее собой условие трехмерного разрушения.
Дата добавления: 2016-03-15; просмотров: 897;
