МГНОВЕННЫЕ УРАВНЕНИЯ СОСТОЯНИЯ И КРИТЕРИИ ПРОЧНОСТИ
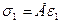 (5.1)
(5.1)
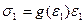 (5.2)
(5.2)
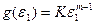 (5.3)
(5.3)
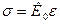 (5.4)
(5.4)
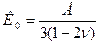 (5.5)
(5.5)
В практике инженерных расчетов чаще других используется следующая эмпирическая зависимость предельного значения 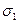 (
( 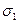 или
или 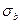 ) от среднего нормального напряжения
) от среднего нормального напряжения  , предложенная Э. Хоеком:
, предложенная Э. Хоеком:
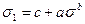 , (5.6)
, (5.6)
где с – значение 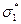 при
при 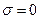 ; a, b – константы, являющиеся функциями температуры, влажности и др.
; a, b – константы, являющиеся функциями температуры, влажности и др.
Для многих горных пород хорошей аппроксимацией может оказаться линейная зависимость, называемая критерием Мора,
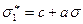 (5.7)
(5.7)
Инженерные расчеты удобно проводить, когда зависимость параметров с, а, b, равно как и K и т в формуле (5.3), от температуры и влажности принята в аналитической форме. Однако таких общепринятых норм в литературе не предложено. Поэтому необходимо руководствоваться соображениями удобства при расчетах с требуемой точностью. Например, в формуле (5.3) часто бывает удобным фиксировать показатель т, а коэффициент K считать линейной функцией, или экспонентой.
2. При сложно-напряженном состоянии упругое деформирование изотропных тел описывается общими уравнениями состояния, называемыми обобщенным законом Гука:
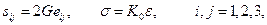 (5.8)
(5.8)
т.е. компоненты девиаторов напряжений и деформаций, среднее нормальное напряжение и относительное изменение объема пропорциональны или в эквивалентной форме:
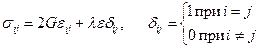 (5.9)
(5.9)
т.е. компоненты тензора напряжений суть линейные функции компонент тензора деформаций и обратно:
 (4.10)
(4.10)
где 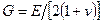 - модуль сдвига;
- модуль сдвига; 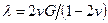 - коэффициент Ламе. Характерно, что коэффициенты пропорциональности в этих общих уравнения определяют параметрами, получаемым при простых видах нагружения.
- коэффициент Ламе. Характерно, что коэффициенты пропорциональности в этих общих уравнения определяют параметрами, получаемым при простых видах нагружения.
На основании уравнений (5.8) и формул (1.21), (1.40) выведено полезное соотношение
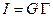 , (5.8/)
, (5.8/)
т.е. интенсивность касательных напряжений Т пропорциональна интенсивности деформаций сдвига Г.
Более сложными уравнениями описывается неупругая деформация. В приложениях обычно пользуются упрощенными теориями пластичности.
Наиболее широкое применение получили уравнения состояния деформационной теории пластичности
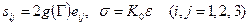 (5.11)
(5.11)
или в эквивалентной форме
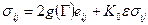 , (5.12)
, (5.12)
и обратная зависимость
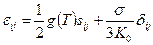 , (5.13)
, (5.13)
которые являются простым обобщением уравнений (5.8) – (5.10).
В уравнениях (5.11) – (5.13) функция g(Г) в силу соотношения 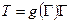 и формулы (5.2) определяется по виду функции
и формулы (5.2) определяется по виду функции 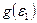 , например, подобно формуле (5.3):
, например, подобно формуле (5.3):
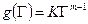 .
.
Функция 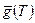 служит коэффициентом в обратном соотношении
служит коэффициентом в обратном соотношении 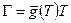 : например, для степенного закона (5.3)
: например, для степенного закона (5.3)
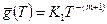 ,
,
где 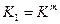 .
.
В случае несжимаемого тела (v = 0,5) уравнения состояния принимают вид
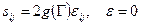 .
.
В состояния пластического течения (см. рис.42 участок АВ), например, при обобщенном критерии Губера – Мизеса, характеризующим переход к пластическим деформациям,
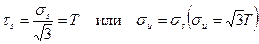 ,
,
3. Условие перехода какого-либо элемента нагруженного твердого тела в состояние хрупкого разрушения или пластического течения, когда в известной мере исчерпывается несущая способность, принято называть критерием прочности при кратковременном монотонном нагружении.
Поэтому в общем случае критерий прочности определяется некоторой предельной поверхностью 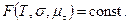
Предложено много различных критериев прочности при сложно-напряженном состоянии изотропных тел [17]. В инженерных расчетах чаще других применяют критерий Шлейхера – Надаи
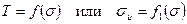 , (4.15)
, (4.15)
где вид функции в правой части устанавливается экспериментально по данным опытов для конкретных материалов.
В частности, при 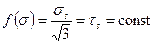 из (4.15) следует критерий Губера – Мизеса (4.14) или эквивалентный ему по форме энергетический критерий. Оба этих критерия основаны на гипотезе, по которой процесс разрушения зависит главным образом от изменения формы элемента тела.
из (4.15) следует критерий Губера – Мизеса (4.14) или эквивалентный ему по форме энергетический критерий. Оба этих критерия основаны на гипотезе, по которой процесс разрушения зависит главным образом от изменения формы элемента тела.
При достижении потенциальной энергией формоизменения элемента тела предельного состояния наступает его разрушение или переход к пластической деформации.
Если 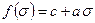 , то из условия (4.15) следует обобщенный критерии Мора
, то из условия (4.15) следует обобщенный критерии Мора 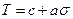 . Используя формулы разд. .2, критерий (4.15) можно сформулировать в терминах максимального касательного
. Используя формулы разд. .2, критерий (4.15) можно сформулировать в терминах максимального касательного 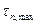 и нормального
и нормального 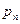 напряжений:
напряжений:
 .
.
Например, относительно главных координатных осей при условии 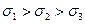 , обобщая соотношение (4.6), можно принять
, обобщая соотношение (4.6), можно принять
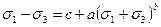 .
.
4. При изучении анизотропии горных пород чаще всего ограничиваются изучением свойств горных пород в плоскости, параллельной напластованию, и плоскости, перпендикулярной к напластованию, считаю любое из направлений в этих плоскостях эквивалентным в отношении механических свойств. Такие тела принято называть трансверсально-изотропными.
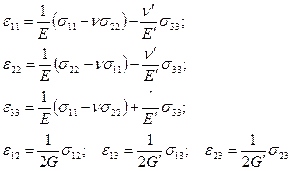 (4.16)
(4.16)
где 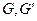 - модули сдвига в плоскости
- модули сдвига в плоскости 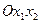 и в перпендикулярных к ней плоскостях.
и в перпендикулярных к ней плоскостях.
Для большинства горных пород модули сдвига рекомендуется вычислять по формулам
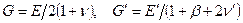 ,
,
где 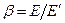 - основной параметр анизотропии.
- основной параметр анизотропии.
Известно, что прочность горных пород на сжатие существенно отличается от прочности на растяжение или сдвиг.
Сравнительно простым критерием прочности может служить, например, следующий [25]:
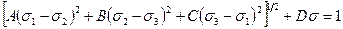 ,
,
который представляет собой обобщение критерия Мора (4.6) относительно главных направлений.
Для хрупкого тела, подчиняющегося этому условию, должно выполняться следующее соотношение между пределами прочности на растяжение  и сжатие
и сжатие 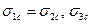 в плоскости напластования
в плоскости напластования 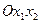 и направлении
и направлении 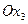 , перпендикулярном к ней:
, перпендикулярном к ней:
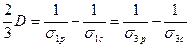 .
.
Постоянные А, В и С связаны с пределами прочности формулами вида

Предложены и более сложные критерии разрушения анизотропных тел [25], содержащие большое число констант, подлежащих определению на основании опытных данных. Однако использование их вряд ли возможно из-за больших трудностей в проведении опытов.
Из (4.17) как частный случай следует критерий прочности для изотропных тел 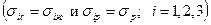 :
:
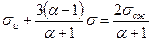 , (4.17’)
, (4.17’)
где 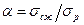 .
.
Этот критерий является одним из весьма полезных разновидностей общего критерия (4.15) для оценки прочности горных пород и цементного камня.
Опытами доказано, что деформация объема и величина предельного напряжения горной породы зависят исключительно от эффективных напряжений
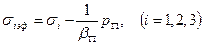 ,
,
где 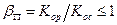 - коэффициент порового давления, характеризующий различную сопротивляемость скелета породы растяжению и сжатию;
- коэффициент порового давления, характеризующий различную сопротивляемость скелета породы растяжению и сжатию; 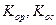 - модули объемной деформации расширения и сжатия соответственно. В это же время установлено, что изменение формы элемента тела не зависит от порового давления.
- модули объемной деформации расширения и сжатия соответственно. В это же время установлено, что изменение формы элемента тела не зависит от порового давления.
Следовательно, для учета поровых (пластовых) давлений необходимо во всех приведенных выше уравнениях состояния и критериях прочности нормальные напряжения 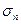 и среднее давление
и среднее давление 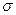 заменить эффективными напряжениями
заменить эффективными напряжениями 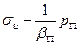 и
и 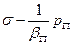 , оставив без изменения касательные напряжения
, оставив без изменения касательные напряжения 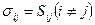 .
.
Например, закон Гука (4.10) и критерий прочности (4.15) перепишутся в виде
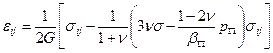 ; (4.10’’)
; (4.10’’)
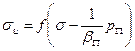 . (4.15’’)
. (4.15’’)
В таком случае все исходные уравнения, включая и уравнения движения (1.45), будут содержать суммарные (тотальные) напряжения 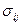 .
.
Для глин и глинистых пород, склонных к набуханию, компоненты деформации 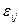 в уравнениях состояния (4.10’) необходимо дополнить слагаемыми
в уравнениях состояния (4.10’) необходимо дополнить слагаемыми  , где
, где 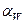 - коэффициент объемного расширения при увлажнении породы;
- коэффициент объемного расширения при увлажнении породы; 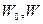 - начальная и текущая влажность породы.
- начальная и текущая влажность породы.
Аналогично учитывается расширение (сжатие) любого твердого тела при нагревании (охлаждении) введением в уравнения состояния слагаемых 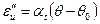 , где
, где  - коэффициент объемного расширения при нагревании;
- коэффициент объемного расширения при нагревании;  ºС,
ºС, 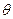 ºС – начальная и текущая температура тела.
ºС – начальная и текущая температура тела.
Дата добавления: 2016-03-15; просмотров: 719;
