Физические величины и шкалы измерений

Физические величины, методы и средства измерений

Физические величины и шкалы измерений

Все объекты окружающего мира характеризуются своими свойствами. Свойство – это философская категория, выражающая такую сторону объекта (явления, процесса), которая обуславливает его различие или общность с другими объектами (явлениями, процессами) и обнаруживается в его отношениях к ним. Свойство – категория качественная. Для количественного описания различных свойств процессов и физических тел вводится понятие величины. Величина – это свойство чего-либо, что может быть выделено среди других свойств и оценено тем или иным способом, в том числе и количественно. Величина не существует сама по себе, она имеет место лишь постольку, поскольку существует объект со свойствами, выраженными данной величиной (рис. 1.1).

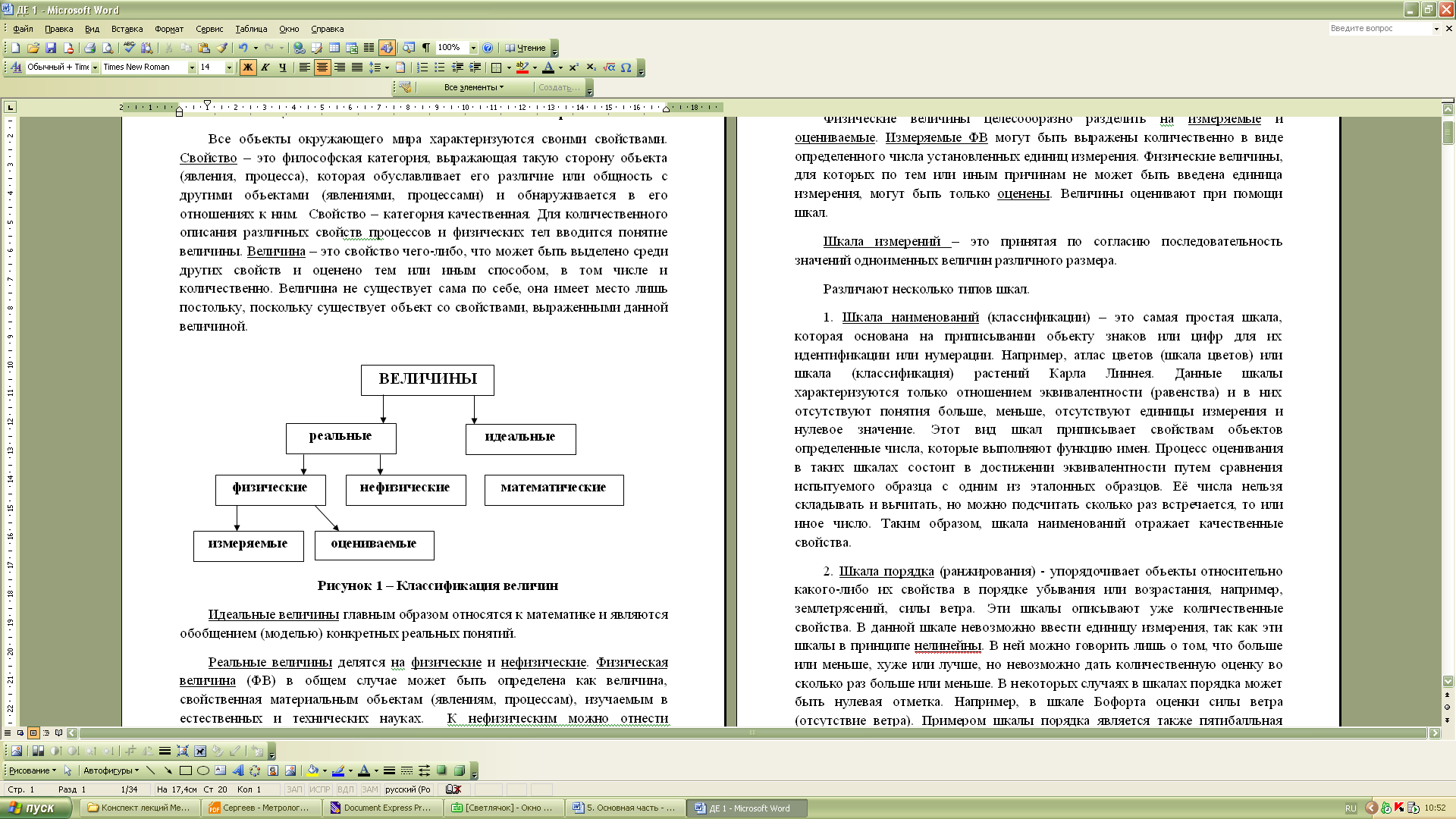
Рис. 1.1. Классификация величин

Идеальные величины главным образом относятся к математике и являются обобщением (моделью) конкретных реальных понятий.

Реальные величины делятся на физические и нефизические. Физическая величина (ФВ) в общем случае может быть определена как величина, свойственная материальным объектам (явлениям, процессам), изучаемым в естественных и технических науках. К нефизическим можно отнести величины, присущие общественным (нефизическим) наукам – философии, социологии, экономике и т. д.

Физическая величина (ФВ) – характеристика одного из свойств физического объекта (физической системы, явления, процесса), общая в качественном отношении для многих физических объектов, но в количественном отношении индивидуальна для каждого объекта.

Физические величины целесообразно разделить на измеряемые и оцениваемые. Измеряемые ФВ могут быть выражены количественно в виде определенного числа установленных единиц измерения. Физические величины, для которых по тем или иным причинам не может быть введена единица измерения, могут быть только оценены. Величины оценивают при помощи шкал.

Шкала измерений – это принятая по согласию последовательность значений одноименных величин различного размера.

Различают несколько типов шкал.

1. Шкала наименований (классификации) – это самая простая шкала, которая основана на приписывании объекту знаков или цифр для их идентификации или нумерации. Например, атлас цветов (шкала цветов) или шкала (классификация) растений Карла Линнея. Данные шкалы характеризуются только отношением эквивалентности (равенства) и в них отсутствуют понятия больше, меньше, отсутствуют единицы измерения и нулевое значение. Этот вид шкал приписывает свойствам объектов определенные числа, которые выполняют функцию имен. Процесс оценивания в таких шкалах состоит в достижении эквивалентности путем сравнения испытуемого образца с одним из эталонных образцов. Её числа нельзя складывать и вычитать, но можно подсчитать сколько раз встречается, то или иное число. Таким образом, шкала наименований отражает качественные свойства.

2. Шкала порядка (ранжирования) упорядочивает объекты относительно какого-либо их свойства в порядке убывания или возрастания, например, землетрясений, силы ветра. Эти шкалы описывают уже количественные свойства. В данной шкале невозможно ввести единицу измерения, так как эти шкалы в принципе нелинейны. В ней можно говорить лишь о том, что больше или меньше, хуже или лучше, но невозможно дать количественную оценку во сколько раз больше или меньше. В некоторых случаях в шкалах порядка может быть нулевая отметка. Например, в шкале Бофорта оценки силы ветра (отсутствие ветра). Примером шкалы порядка является также пятибалльная шкала оценки знаний учащихся. Ясно, что «пятерка» характеризует лучшее знание предмета, чем «тройка», но во сколько раз лучше, сказать невозможно. Другими примерами шкалы порядка являются шкала силы землетрясений (например, шкала Рихтера), шкалы твердости, шкалы силы ветра. Некоторые из этих шкал имеют эталоны, например, шкалы твердости материалов. Другие шкалы не могут их иметь, например, шкала волнения моря.

Шкалы порядка и наименований называют неметрическими шкалами.

3. Шкала интервалов (разностей) содержит разность значений физической величины. Для этих шкал имеют смысл соотношения эквивалентности, порядка, суммирования интервалов (разностей) между количественными проявлениями свойств. Шкала состоит из одинаковых интервалов, имеет условную (принятую по соглашению) единицу измерения и произвольно выбранное начало отсчета – нуль. Примером такой шкалы являются различные шкалы времени, начало которых выбрано по соглашению (от Рождества Христова, от переселения пророка Мухаммеда из Мекки в Медину). Другими примерами шкалы интервалов являются шкала расстояний и температурная шкала Цельсия. Результаты измерений по этой шкале (разности) можно складывать и вычитать.

4. Шкала отношений – это шкала интервалов с естественным (не условным) нулевым значением и принятые по соглашению единицы измерений. В ней нуль характеризует естественное нулевое количество данного свойства. Например, абсолютный нуль температурной шкалы. Это наиболее совершенная и информативная шкала. Результаты измерений в ней можно вычитать, умножать и делить. В некоторых случаях возможна и операция суммирования для аддитивных величин. Аддитивной называется величина, значения которой могут быть суммированы, умножены на числовой коэффициент и разделены друг на друга (например, длина, масса, сила и др.). Неаддитивной величиной называется величина, для которой эти операции не имеют физического смысла, например, термодинамическая температура. Примером шкалы отношений является шкала масс – массы тел можно суммировать, даже если они не находятся в одном месте.

5. Абсолютные шкалы – это шкалы отношений, в которых однозначно (а не по соглашению) присутствует определение единицы измерения. Абсолютные шкалы присущи относительным единицам (коэффициенты усиления, полезного действия и др.), единицы таких шкал являются безразмерными. Результаты измерений имеют наибольшую достоверность, информативность и чувствительность к неточности измерений.

6. Условные шкалы – шкалы, исходные значения которых выражены в условных единицах. К таким шкалам относятся шкалы наименований и порядка.

Шкалы разностей, отношений и абсолютные называются метрическими (физическими) шкалами.

Для более детального изучения ФВ необходимо классифицировать и выявить общие метрологические особенности их отдельных групп.

По видам явлений ФВ делятся на следующие группы:

· вещественные, т. е. описывающие физические и физико-химические свойства веществ, материалов и изделий из них. К этой группе относятся масса, плотность, электрическое сопротивление, емкость, индуктивность и др.;

· энергетические, т. е. величины, описывающие энергетические характеристики процессов преобразования, передачи и использования энергии. К ним относятся ток, напряжение, мощность, энергия;

· характеризующие протекание процессов во времени. К этой группе относят различного рода спектральные характеристики, корреляционные функции и т. д.

По принадлежности к различным группам физических процессов ФВ делятся на:

· пространственно-временные;

· механические;

· тепловые;

· электрические и магнитные;

· акустические;

· световые;

· физико-химические;

· ионизирующих излучений;

· атомной и ядерной физики.

По степени условной независимости от других величин ФВ делятся на:

· основные;

· производные;

· дополнительные.

По наличию размерности ФВ делятся на:

· размерные;

· безразмерные.

Когда интересуются количественным содержанием свойства в объекте, говорят о размере физической величины. Это ее количественная характеристика. Чтобы иметь представление о физической величине с количественной точки зрения, необходимо выразить ее числом, т. е. измерить. Измерить физическую величину – значит найти отношение ее размера к размеру той же величины, условно, обычно по международному соглашению, принятому за единицу измерения. Такое сравнение измеряемой величины с однородной ей величиной, размер которой известен, является главной частью любого процесса измерения. Метрология имеет дело с измеримыми физическими величинами. Физическую величину можно измерить, если выделить ее среди других, выбрать единицу для измерений и воплотить ее в средстве измерений.

Единицей физической величины называется такая физическая величина, которой приписывается числовое значение, равное 1.

Оценка физической величины в виде некоторого числа принятых для нее единиц называется значением физической величины. Значения физической величины получают в результате ее измерения или вычисления. В соответствии с основным уравнением измерения:

Q = n [Q]; (1.1)

где Q – значение физической величины; n – числовое значение измеряемой величины в принятых единицах; [Q] – выбранная для измерений единица.

Числовое значение конкретной физической величины изменяется в зависимости от размера выбранной единицы, в то время как размер этой величины остается одним и тем же.

Размер нужно отличать от значения физической величины – конкретного выражения размера в виде определенного числа выбранных единиц измерения (например, 2 метра, 200 люкс).

Отвлеченное число, входящее в значение физической величины, называется ее числовым значением (в последнем примере – это 2 и 200).

Размер величины существует реально, независимо от того, известен он или нет, и не зависит от выбора единицы измерения. Числовое же значение зависит. Например, 0,001 км; 1 м; 100 см; 1000 мм (четыре варианта представления одного размера) – это значения измеряемой величины.