Общие принципы комбинаторики
Классическое определение вероятности, по существу, является не определением, а методом подсчета вероятностей событий в опытах, обладающих симметрией возможных исходов. Для подсчета вероятностей по классической формуле обычно используют методы комбинаторики.
Комбинаторика – это раздел математики, посвященный решению задач выбора и расположения элементов в соответствии с каким-либо правилом. Например, сколькими способами можно выбрать 6 карт из колоды, состоящей из 36 карт; или сколькими способами можно составить очередь, состоящей из10 человек и т.д. Каждое правило в комбинаторике определяет способ построения некоторой конструкции, составленной из элементов исходного множества и называемой комбинацией. Основная цель комбинаторики состоит в подсчете количества комбинаций, которые можно составить из элементов исходного множества в соответствии с заданным правилом. При решении комбинаторных задач используются два правила: принцип умножения и принцип сложения.
Принцип умножения. Если элемент А можно выбрать из некоторого множества m способами и если после каждого такого выбора элемент B можно выбрать n способами, то пара элементов (А,В) в указанном порядке может быть выбрана (m×n) способами.
Пример 1.4. Из пункта А в пункт В ведут 3 дороги, а из пункта В в пункт С – 4 дороги. Сколькими способами можно совершить поездку из А в С через В?
Решение. В пункте А есть 3 способа выбора дороги в пункт В, а в пункте В есть 4 способа попасть в пункт С. Согласно принципу умножения, существует 3×4=12 способов попасть из пункта А в пункт С.
Принцип умножения легко обобщается на случай произвольного конечного множества.
Пример 1.5. Сколько четырехзначных чисел можно составить из цифр: 1, 2, 3, 4 и 5, если: а) цифры не повторяются; б) повторение допустимо; в) числа должны быть нечетные и без повторения.
Решение. а) Первую цифру можно выбирать 5-ю способами. Так как в числе цифры не повторяются, то вторую цифру уже можно выбрать из четырех оставшихся 4-мя способами. Далее получаем, что третью цифру можно выбрать 3-мя способами и четвертую – двумя. Таким образом, число возможных четырехзначных чисел равно N=5×4×3×2=120.
б) Так как повторения допустимы, то каждую цифру можно выбирать каждый раз из 5 имеющихся цифр, т.е. пятью способами. Тогда число возможных чисел равно N=5×5×5×5=54=625.
в) У нечетного числа последняя цифра нечетная, т.е. в данном случае может быть либо 1, либо 3, либо 5. Поэтому на это место можно поставить любую из этих трех чисел. После этого на оставшиеся места можно поставить: четыре цифры, три цифры и две цифры, ибо никакие из пяти цифр нельзя использовать более одного раза. Таким образом, N=3×4×3×2=72.
Принцип сложения. Если элемент А можно выбрать из некоторого множества m способами, а другой элемент B – n способами, причем выборы А и В таковы, что взаимно исключают друг друга и не могут быть выбраны одновременно, то выбор какого-либо одного из этих элементов (либо А, либо В) можно осуществить (m+n) способами.
Пример 1.6. Имеется 20 изделий 1-го сорта и 30 изделий 2-го сорта. Необходимо выбрать два изделия одного сорта. Сколько способов выбора возможно в данной ситуации, если учитывается порядок выбора изделий?
Решение. По принципу умножения два изделия 1-го сорта можно выбрать 20×19=380 способами. Аналогично два изделия 2-го сорта можно выбрать 30×29=870 способами. Согласно условию задачи следует выбирать два изделия одного сорта, не важно какого, т.е. либо 1-го, либо 2-го. Эти действия взаимно исключают друг друга. Поэтому общее число способов выбора изделий одного сорта равно 380+870=1250.
При решении комбинаторных задач важно уметь выделять случаи, где можно использовать те или иные формулы. Пусть имеется множество, состоящее из n элементов, например, урна, содержащая n различных шаров. Выборкой будем называть любую совокупность k элементов этого множества; другими словами, выбор k шаров из урны. Однако, при постановке такого эксперимента должно быть строго оговорено, каким способом производится выбор и что понимается под различными выборками.
Существует две принципиально различные схемы выбора. В первой схеме выбор осуществляется без возвращения элементов. Это означает, что в выборке невозможны повторения элементов. Во второй схеме выбор осуществляется по-элементно с обязательным возвращением отобранного элемента при каждом шаге. Это означает, что в выборке возможны повторения.
После того. как выбор тем или иным способом осуществлен, отобранные элементы могут быть либо упорядочены, либо неупорядочены. В первом случае, выборки, состоящие из одних и тех же элементов, но отличающиеся порядком следования этих элементов, объявляются различными. Во втором случае порядок следования элементов не принимается во внимание, и такие выборки объявляются тождественными.
В результате получаются четыре различные постановки эксперимента по выбору k элементов из общего числа n элементов некоторого множества.
| Набор Выбор | Упорядоченный | Неупорядоченный |
| Без возвращений (без повторений) | Размещения
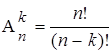
| Сочетания
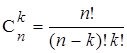
|
| С возвращением (с повторениями) | Размещения с повторениями
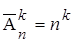
| Сочетания с повторениями
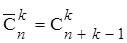
|
Эту таблицу для случая n=3, k=2 можно записать следующим образом:
| Набор Выбор | Упорядоченный | Неупорядоченный |
| Без возвращений (без повторений) | (1,2) (1,3) (2,3) (2,1) (3,1) (3,2) | (1,2) (1,3) (2,3) |
| С возвращением (с повторениями) | (1,2) (2,1) (1,1) (1,3) (3,1) (2,2) (2,3) (3,2) (3,3) | (1,2) (1,3) (2,3) (1,1) (2,2) (3,3) |
Подобные задачи возникают в статистической физике, например, при изучении распределения n частиц (это могут быть молекулы, электроны, протоны, нейтроны и другие частицы) по k состояниям (это могут быть энергетические уровни). Так, статистика Максвелла-Больцмана характеризуется как система k различных частиц (например, молекулы газа), каждая из которых может находится в одном из n состояний вне зависимости от того, где при этом находятся остальные частицы. Статистика Бозе-Эйнштейна определяется как система k неразличимых (тождественных) частиц, каждая из которых независимо от остальных может находиться в одной из n состояний. Статистика Ферми-Дирака определяется как статистика Бозе-Эйнштейна, в которой дополнительно действует принцип запрета Паули, требующий, чтобы в каждом состоянии находилось не более одной частицы. Отметим, что случай различных частиц, подчиняющихся принципу запрета, в физике не встречается.
| Набор Выбор | Упорядоченный | Неупорядоченный |
| С запретом (без повторений) | Статистика Ферми-Дирака | |
| Без запрета (с повторениями) | Статистика Максвелла-Больцмана | Статистика Бозе-Эйнштейна |
 | |
 |
Дата добавления: 2016-03-10; просмотров: 4719;
