Классическое определение вероятности. Изложим классическое определение вероятности, служившее основой этой науки со времен ее зарождения в XVII в

Изложим классическое определение вероятности, служившее основой этой науки со времен ее зарождения в XVII в. (Б. Паскаль, П. Ферма, Я. Бернулли) вплоть до 20-30-х годов XX в., когда теория вероятностей встала на путь аксиоматического метода.

Чтобы охарактеризовать вероятность события числом, нужно установить единицу измерения вероятности. Здесь поступают следующим образом: достоверному событию приписывают вероятность, равную единице; невозможному – равную нулю. Таким образом, вероятность P(A) события А должна удовлетворять следующим условиям:

1^о. P(A)=1, если А – достоверное событие;

2^о. P(A)=0, если А – невозможное событие;

3^о. 0<P(A)<1, если А – случайное событие.

Классическое определение вероятности основано на понятии равновозможности (или равновероятности). Это понятие относится к числу первичных, не подлежащим формальному определению. Оно лишь поясняется рядом простых и доступных примеров. Например, выпадение одной из сторон монеты или одной из граней игральной кости – равновозможные события. Это утверждение опирается на повседневную практику и симметрию изучаемого объекта. Симметрия возможных исходов чаще всего наблюдается в искусственно организованных опытах, где приняты специальные меры для ее обеспечения (например, тасовка карт или костей домино, которая для того и производится, чтобы каждая из них могла быть выбрана с одинаковой вероятностью; или же приемы случайного выбора группы изделий для контроля качества в производственной практике). В таких опытах подсчет вероятностей производится проще всего. Не случайно первоначальное свое развитие теория вероятностей получила на материале азартных игр.

Говорят, что несколько событий образуют полную группу, если в результате опыта неизбежно должно появится хотя бы одно из них. Примеры событий, образующих полную группу: 1) появление "1", "2", "3", "4", "5", "6" очков при бросании игральной кости; 2) "два попадания", "два промаха", "одно попадание" при двух выстрелах по мишени; 3) "появление хотя бы одного белого", "появление хотя бы одного черного" шара при вынимании двух шаров из урны. Несовместные события, образующие полную группу, называются элементарными событиями (или элементарными исходами). Отметим, что события первого и второго примеров являются элементарными, а третьего – нет, т.к. они совместны.

Элементарные исходы, в которых интересующее нас событие наступает, называются благоприятствующими этому событию. Например, при бросании одной игральной кости для события, состоящего в том, что выпадет не более двух очков, благоприятствующими элементарными исходами будут выпадение "1" или "2" очков.

Классическое определение вероятности: вероятностью события А называется отношение числа m благоприятствующих этому событию исходов к общему числу n всех равновозможныхнесовместных элементарных исходов, образующих полнуюгруппу:

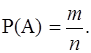
Пример 1.2. В урне находится 5 шаров, из которых 2 белых и 3 черных. Из урны наугад вынимают один шар. Найти вероятность того, что этот шар будет белым.

Решение. Обозначим через А интересующее нас событие, т.е. появление белого шара. Общее число всех равновозможных несовместных элементарных исходов, образующих полную группу, равно n=5; из них благоприятствующих событию А будет m=2. Следовательно, вероятность события А равна

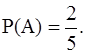
Прием непосредственного подсчета вероятностей был положен в основу т.н. "классической" теории вероятностей и долгое время считался универсальным. Опыты, не обладающие симметрией возможных исходов, искусственно сводились к "классической схеме". Несмотря на ограниченную сферу практического применения этой схемы, она все же представляет известный интерес, т.к. именно на ней легче всего познакомится со свойствами вероятностей.

"Ахиллесовой пятой" классического определения вероятности является понятие равновозможности, т.е. вопрос о том являются ли рассматриваемые события равновозможными или нет. Ответить на эти вопросы не всегда легко. На заре создания теории вероятностей здесь было наделано немало ошибок.

Пример 1.2. (Ошибка Даламбера). Бросаются две монеты. Какова вероятность того, что обе монеты выпадут "гербом" вверх? При решении этой задачи один из выдающихся французских ученых Ж. Даламбер рассуждал следующим образом. При подбрасывании двух монет возможны три случая: А₁={два герба}, A₂={две решки}, A₃={герб и решка}. Эти события находятся в равных условиях, поэтому их вероятности равны 1/3. Однако это неверно. Эти события не являются равновозможными. Последнее событие, как показали наблюдения, вдвое вероятнее каждого из остальных. Решим эту задачу иначе. Для этого рассмотрим следующие события: В₁={на первой монете герб, на второй – герб}, В₂={на первой монете решка, на второй – решка}, В₃={на первой монете герб, на второй – решка}, В₄={на первой монете решка, на второй – герб}. Все эти события несовместны, равновозможны и образуют полную группу. Следовательно вероятность события В₁ равна 1/4, что совпадает с результатами наблюдений.

Пример 1.3. (Задача де Мере). Бросаются три игральные кости. Что вероятнее: получить в сумме выпавших очков 11 или 12? Эта задача была одно из первичных, на основании которых формировались понятия и методы теории вероятностей. Утверждают, что с такой задачей обратился однажды к Б. Паскалю шевалье де Мере. Он заявил Паскалю, что согласно логике обе эти суммы должны появляться одинаково часто, но наблюдения показали, что сумма 11 появляется все же чаще, чем 12. Обоснование де Мере звучит довольно убедительно на первый взгляд. Числа 11 и 12 могут быть разложены на сумму трех целых положительных чисел лишь шестью способами: 11 = 1+5+5 = 1+4+6 = 2+3+6 = 2+4+5 = 3+3+5 = 3+4+4 и 12 = 1+5+6 = 2+4+6 = 2+5+5 = 3+4+5 = 3+3+6 = 4+4+4. Отсюда, по мнению де Мере, вытекает равновероятность обоих сумм. Но почему 11 выпадает все же чаще? Дело в том, что исходы, которые рассматривал де Мере, не являются равновозможными. Необходимо учитывать, на какой из трех костей выпадают те или иные очки. Поэтому комбинация (1,4,6) может возникнуть при шести различных исходах бросания, комбинация (1,5,5) – при трех, а (4,4,4) – при единственном исходе.

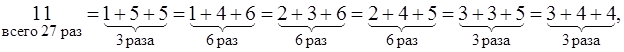
Нетрудно подсчитать, что событию А={сумма очков равна 11} благоприятствует 27 исходов, а событию В={сумма очков равна 12} – 25 исходов. Поскольку при подбрасывании трех игральных костей возможны 6³=216 несовместных и равновозможных исходов, образующих полную группу, то по формуле классической вероятности получаем

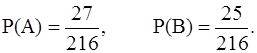
Отсюда видно, что P(A)>P(B).