Расчет выправки кривой

Рассматривается расчет выправки расстроенной в процессе эксплуатации кривой, основанный на теории нормалей /4/.

Эпюра проектных и натурных стрел в этом случае будет иметь вид, представленный на рис. 8.1.1 /4, рис. 50/.

L

f_i F_i

L_I

0 C I

L₁ L_c

Рисунок 8.1.1 – Эпюра проектных и натурных стрел

Предварительные расчеты.

Исходными данными для проведения расчета являются: измеренные с шагом а натурные стрелы f_i , угол поворота кривой φ в градусной мере, пикетажное значение начальной точки измерения стрел, средняя V_ср и максимальная V_max скорости движения поездов в данной кривой.

Расчеты проводятся в табличной форме, /4, табл. 13/, где в гр.1 заносится пикетажное значение точки кривой, в которой измерялась натурная стрела, в гр.2 – номер этой точки, в гр.3 записываются измеренные натурные стрелы f_i, а в гр.4 - исправленные натурные стрелы f_{i испр}. Следует помнить, что нумерация точек начинается с нуля; номер последней точки измерения стрел – N.

Проверка правильности измерения натурных стрел проводится по формуле

, (8.1.1)

где φ – угол поворота кривой, радиан; a – шаг деления кривой, мм (обычно принимается a =10000 мм); S'_теор – первая теоретическая сумма натурных стрел, мм.

Из формулы (8.1.1) определяем S'_теор

В таблице вычислений первая сумма измеренных натурных стрел (S'_изм) равняется сумме значений измеренных натурных стрел в гр.3.

Погрешность измерения стрел (δ S') не должна превышать величину:

δ S' <=1,5√N+1 , где N+1 – количество измеренных стрел.

т.е. δ S' = |S'_изм – S'_теор|<=1,5√N+1

Если полученная погрешность удовлетворяет данному условию, исправляем значения измеренных натурных стрел (меняем значение стрелы в данной точке не более, чем на 1 мм), доводя сумму их значений до величины S'_теор. Исправленные значения натурных стрел заносятся в гр.4. Далее все расчеты ведутся с исправленными натурными стрелами.

Подсчитываются первые (S') и вторые (S'')суммы натурных исправленных стрел и записываются соответственно в гр. 5 и гр.6. При этом сумма значений гр.4 должна быть равна значению S' в последней строке гр.5, а сумма значений гр.5 - значению S'' в последней строке гр.6. Сумма значений S'' гр.6 представляет собой тройную сумму натурных исправленных стрел - S'''.

Определение положения характерных точек.

Находим расстояние от начальной точки измерения стрел до центра тяжести эпюры натурных стрел (L_c):

. (8.1.2)

Вычисляем значение квадрата радиуса момента инерции эпюры натурных стрел

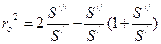. (8.1.3)

Длину переходной кривой назначаем из условия обеспечения нормативного уклона отвода возвышения наружного рельса:

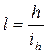, (8.1.4)

где l – длина переходной кривой, м; h – возвышение наружного рельса, мм; i_h – уклон отвода возвышения наружного рельса, ‰.

Согласно /СТН Ц 01-95/, нормативное значение i_h = 1‰.

Возвышение наружного рельса в кривой определим как максимальное из условия равномерного износа рельсов (8.1.5) и условия комфортабельного движения пассажиров (8.1.6):

; (8.1.5)

, (8.1.6)

где R – радиус круговой кривой, м;

Определяем длину круговой кривой (L) при n_ср = 0

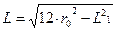. (8.1.7)

г) Определяем проектную стрелу в пределах круговой кривой

(8.1.8)

и соответствующий ей радиус

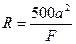. (8.1.9)

д) Расстояние от последней точки I до начала выходной переходной кривой

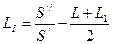. (8.1.10)

е) Определяем пикетажные значения характерных точек:

;

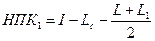(8.1.11)

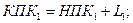
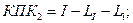
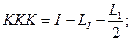
Все длины и пикетажные значения характерных точек вычисляются в дам с точностью до 0,001 м.

Определение проектных стрел.

а) Рассчитываем проектные стрелы для точек в пределах переходных кривых:

первой

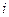, =1,2,3,…

второй

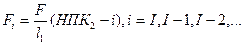(8.1.12)

б) Проектные стрелы заносятся в графу 7 и корректируются так, чтобы

.

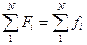Расчет сдвигов.

а) Находим разность проектных и натурных стрел в каждой точке деления 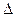f_i = f_i – F_i и записываем в графу 8.

б) В столбец 9 записываются удвоенные разности стрел со сдвигом на одну точку вперед по ходу нумерации точек.

в) В графу 10 записываем сумму удвоенных разностей, а в графу 11 сумму сумм удвоенных разностей. Следовательно в графе 11 запишется величина сдвига со своим знаком. Напомним, что знак минус показывает сдвиг внутрь, а плюс – наружу кривой.

Так как , то нормаль в последней точке должна быть равна нулю.

г) Полученную невязку распределяем на все точки.

Невязка в последней точке возникает из-за округления проектных стрел до 1 мм.

Невязку, в зависимости от её абсолютной величины, можно распределять по линейному или параболическому закону.