СХЕМА СИЛ И УРАВНЕНИЯ ДВИЖЕНИЯ НА РАЗЛИЧНЫХ ЭТАПАХ ВЗЛЕТА
При разбеге на самолет действуют аэродинамические силы:
- подъемная сила крыла Y;
- сила лобового сопротивления X;
- вес самолета G;
- сила тяги силовой установки Р;
- нормальная реакция земли N=N1+N2;
- сила трения колес о земную поверхность F=F1+F2 (Рис. 5).
Как уже говорилось ранее, в аэродинамике и динамике полета самолета рассматривается движение центра тяжести относительно внешней среды и движение частей самолета вокруг центра тяжести. В данном случае рассмотрим движение центра тяжести.
Уравнения движения центра тяжести самолета при разбеге имеют вид:
Условие разгона
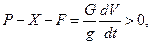 (7.21)
(7.21)
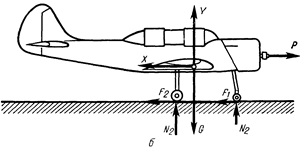
Рис. 5 Схема сил, действующих на самолет ТЛ-2000 на взлете
условие прямолинейного разгона
Y+N-G=0. (7.22)
В уравнении (7.21) сила тяги должна быть больше лобового сопротивления и силы трения колес вместе взятых или произведение массы - 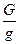 - на прирост скорости должно быть больше нуля. В уравнении (7.22) вес самолета должен быть равен сумме подъемной силы и реакции земли. Силу тяги следует считать направленной по скорости движения. Силу трения определяют через нормальную реакцию N и коэффициент трения f
- на прирост скорости должно быть больше нуля. В уравнении (7.22) вес самолета должен быть равен сумме подъемной силы и реакции земли. Силу тяги следует считать направленной по скорости движения. Силу трения определяют через нормальную реакцию N и коэффициент трения f
F=Nf. (7.23)
Коэффициент трения f при разбеге на колесах по бетонной ВПП равен 0,03...0,05, а по травянистому грунту - 0,1...0,12.
По мере увеличения скорости полета подъемная сила растет, а нормальная реакция земли уменьшается. Когда подъемная сила становится равной весу самолета, то он отрывается от земли.
На этапах разгона и подъема на самолет действуют следующие силы: подъемная сила Y; вес самолета G; сила тяги Р (Рис. 5).
Уравнения движения центра тяжести самолета при разгоне с подъемом имеют вид:
условие разгона
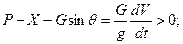 (7.24):
(7.24):
условие прямолинейности полета
Y-Gcos 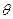 =0. (7.25)
=0. (7.25)
В уравнении (7.24) тяга двигателя Р должна быть больше суммы лобового сопротивления и составляющей силы веса самолета, а в уравнении (7.25) -подъемная сила Y должна быть равна составляющей веса самолета G cos 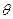 .
.
Уравнения движения (7.24) и (7.25) показывают, что самолет движется прямолинейно (Y=Gcos 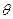 ) и с ускорением. Ускорение равно
) и с ускорением. Ускорение равно
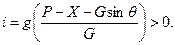
Дата добавления: 2016-03-05; просмотров: 3295;
