Метод моментов (метод условного нуля)
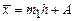 ,
, 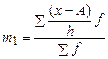 , где m1 – момент первого порядка, h – величина интервала, А – варианта, соответствующая максимальной частоте.
, где m1 – момент первого порядка, h – величина интервала, А – варианта, соответствующая максимальной частоте.
Пример 4.5
По данным таблицы 6 рассчитать среднедушевой доход методом моментов.
Решение: Для нашего примера h=5000; А=17500 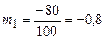
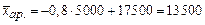 .
.
Таблица 6
| Среднедушевой доход | Количество человек, f | 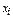
| 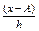
| 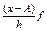
|
| до 5000 | – 3 | – 30 | ||
| 5000 - 10000 | – 2 | – 40 | ||
| 10000 - 15000 | 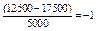
| – 25 | ||
| 15000 - 20000 | 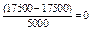
| |||
| 20000 и выше | ||||
| Итого | 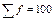
| - | - | 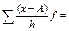
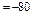
|
Другие виды степенных средних
Из общей формулы 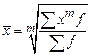 можно получить другие виды степенных средних.
можно получить другие виды степенных средних.
При 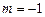 рассчитывается средняя гармоническая
рассчитывается средняя гармоническая
взвешенная – 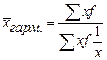 для сгруппированного ряда;
для сгруппированного ряда;
простая – 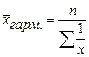 для не сгруппированного ряда.
для не сгруппированного ряда.
Средняя гармоническая используется, когда неизвестны весовые коэффициенты (частоты или частости).
Пример 4.6
Определить среднюю цену реализации товара по данным трех торговых точек (табл.7):
Таблица 7
| Торговая точка | Цена, руб. | Выручка, тыс. руб. |
Решение: 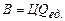 , где В – выручка, Ц – цена единицы продукции.
, где В – выручка, Ц – цена единицы продукции.
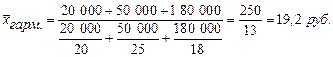
При 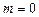 рассчитывается средняя геометрическая
рассчитывается средняя геометрическая
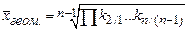 - используется в рядах динамики при расчете среднего темпа роста .
- используется в рядах динамики при расчете среднего темпа роста .
При 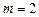 рассчитывается средняя квадратическая
рассчитывается средняя квадратическая
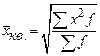 .
.
При 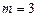 рассчитывается средняя кубическая:
рассчитывается средняя кубическая:
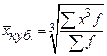 .
.
Средняя квадратическая и средняя кубическая используются для расчета моментов 2–ого и 3–его порядка.
Свойство мажорантности (ранжирование степенных средних): чем больше степень, тем больше средняя.
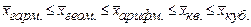
Дата добавления: 2016-03-05; просмотров: 1270;
