Осевое растяжение и сжатие прямолинейного стержня
2.6.1. Построение эпюр продольных сил
Рассмотрим случай осевого растяжения или сжатия, при котором внешние силы действуют по оси стержня. Для определения внутренних усилий (продольных осевых сил) применим метод сечений. Вначале определим реакцию связи RA.
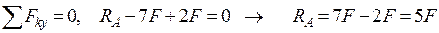 .
.
Проводим сечение n-n, отбрасываем верхнюю часть и рассматриваем равновесие оставшейся части (рис. 2.12). Воздействие отброшенной части заменяем внутренним усилием N1. Под действием двух внешних сил 7F и 2F и внутреннего усилия N1 оставшаяся часть бруса будет находиться в равновесии. Составляем уравнение равновесия в виде суммы проекций всех сил на вертикальную ось и находим N1:
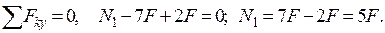
Таким образом, в сечении n-n действует растягивающее усилие, величина которого равна 5F. Очевидно, что такой же результат получится, если сечение провести в любом месте на участке от точки приложения силы 7F до точки А. Рассуждая аналогичным образом, определим внутреннее усилие в сечении m-m. В этом сечении действует сжимающее усилие равное 2F. Принято растягивающее усилие считать положительным, а сжимающее – отрицательным.
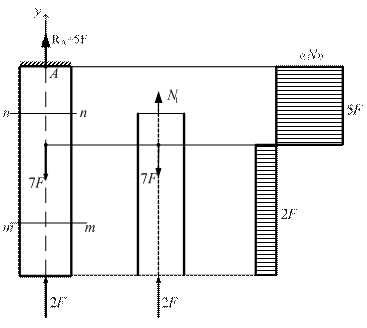
Рис. 2.12
Построим график изменения продольных сил по оси стержня. Базовую ось графика проводим параллельно оси стержня, а значения продольных сил откладываем перпендикулярно оси в выбранном масштабе. Положительные значения откладывают вправо либо вверх, если ось горизонтальная, отрицательные значения – влево либо вниз. Такой график называется эпюрой продольных сил. Этими же правилами будем пользоваться при построении эпюр различных величин, таких как напряжения, крутящие моменты, перемещения и т. д.
2.6.2. Определение нормальных напряжений
в поперечных сечениях стержня
Нанесём на поверхность призматического стержня линии перпендикулярные и параллельные оси и приложим к нему растягивающую осевую силу F (рис. 2.13).

Рис 2.13
Можно заметить, что после деформации линии, нанесённой на стержень, сетки останутся взаимно перпендикулярными, а расстояние между горизонтальными линиями увеличится, при этом они останутся прямыми. Поскольку горизонтальные линии представляют собой след секущей плоскости, то можно сделать вывод о том, что поперечные сечения стержня, плоские и нормальные к его оси до деформации, остались плоскими и нормальными к оси и после деформации. Это очень важная гипотеза сопротивления материалов, которая носит название гипотезы плоских сечений или гипотезы Бернулли.
На основании гипотезы Бернулли можно сделать вывод о том, что в поперечных сечениях стержня действуют только нормальные напряжения, равномерно распределённые по сечению, в противном случае горизонтальные линии не сохраняли бы прямолинейность и не были бы нормальными к оси. Касательные напряжения в этих сечениях отсутствуют, так как углы сетки остались прямыми, что свидетельствует об отсутствии сдвига слоёв материала стержня.
Продольная сила N является равнодействующей нормальных напряжений в поперечном сечении:
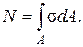 (2.1)
(2.1)
Поскольку σ = сonst, то 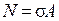 , откуда
, откуда 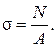 (2.2)
(2.2)
Формула (2.2) применяется и при сжатии с той разницей, что сжимающие напряжения считаются отрицательными.
2.6.3. Определение деформаций
Для большинства конструкционных материалов при нагружении до определённых значений напряжений справедлива следующая зависимость между деформацией стержня и нормальным напряжением:
 (2.3)
(2.3)
где ε – относительное удлинение стержня; 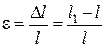 ;
;
∆ℓ – абсолютное удлинение стержня; ℓ – длина образца до деформации;
ℓ1– длина образца после деформации (рис. 2.13).
Зависимость (2.3) носит название закона Гука и формулируется следующим образом: линейные деформации прямо пропорциональны нормальным напряжениям.
Коэффициент Е, зависящий от материала, называется модулем продольной упругости, или модулем упругости первого рода. Он характеризует жёсткость материала, т. е. его способность сопротивляться деформации. Поскольку ε – величина безразмерная, то единица измерения модуля продольной упругости Е та же, что и у напряжения σ, т. е. паскаль. В табл. 2.1 приведены значения Е для некоторых материалов.
| Материал | E, МПа | Материал | E, МПа |
| Сталь | 2×105 … 2,2×105 | Бронза | 1,2×105 |
| Медь | 1×105 | Титан | 1×105 |
| Чугун | 0,75×105 … 1,6×105 | Дерево | 1×105 |
| Алюминий | 0,675×105 | Стеклопластики | 0,18×105…0,4×105 |
Таблица 2.1
Поскольку 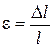 и
и 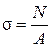 , из формулы (2.3) получаем выражение для определения абсолютного удлинения или укорочения стержня длиной ℓ:
, из формулы (2.3) получаем выражение для определения абсолютного удлинения или укорочения стержня длиной ℓ: 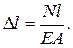 (2.4)
(2.4)
Между продольной и поперечной деформациями существует зависимость:
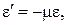 (2.5)
(2.5)
где ε` – относительное поперечное сужение стержня. Коэффициент μ называется коэффициентом Пуассона или коэффициентом поперечной деформации. Значение μ для различных материалов колеблется в пределах от 0 до 0,5. Для всех марок сталей можно принимать значениеμ=0,3. Поскольку 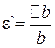 , то полное поперечное сужение (при растяжении) или уширение (при сжатии) определяется по формуле
, то полное поперечное сужение (при растяжении) или уширение (при сжатии) определяется по формуле
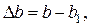
где ∆b – абсолютная поперечная деформация; b – первоначальный поперечный размер; b1 – поперечный размер стержня после деформации.
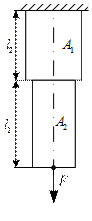 Рис. 2.14
Рис. 2.14
|
В практике часто встречаются стержни переменного сечения, в основном – ступенчатые. У таких стержней полное изменение длины определяется как алгебраическая сумма деформаций его отдельных частей, в пределах которых величины Е, N и A постоянны:
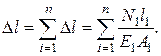
В частности, для приведённой на рис. 2.14 схемы полное удлинение ступенчатого стержня определится как сумма деформаций двух участков:
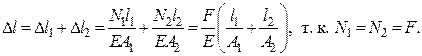
2.6.4. Статически неопределимые задачи при осевом растяжении или сжатии
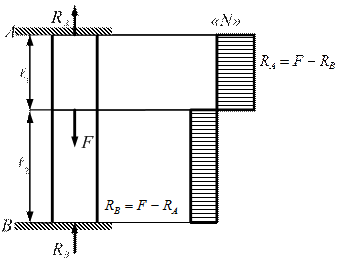 Рис. 2.15
Рис. 2.15
|
Определить реакции и усилия в частях бруса ℓ1 и ℓ2 (рис. 2.15). Сила F растягивает верхнюю часть бруса и сжимает нижнюю. Обозначим реакции заделки RA и R
Уравнение равновесия:
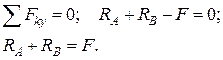
Рассмотрим деформации. Поскольку концы бруса защемлены, то удлинение верхней части равно укорочению нижней, следовательно, 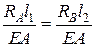 или
или 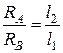 т. е. реакции обратно пропорциональны длинам l1 и l2. Решаем это уравнение совместно с уравнением статики:
т. е. реакции обратно пропорциональны длинам l1 и l2. Решаем это уравнение совместно с уравнением статики:
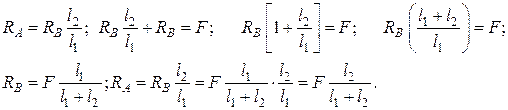
Дата добавления: 2016-03-05; просмотров: 1767;
