Эвольвентное зубчатое зацепление
Построим два зубчатых колеса, находящихся в зацеплении (рис.9.1). Для этого отложим межосевое расстояние 
 , равное сумме радиусов начальных окружностей, а из центров
, равное сумме радиусов начальных окружностей, а из центров 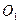 и
и  проведем эти окружности. Начальные окружности касаются друг друга в полюсе Р. Через полюс Р проведем прямую, перпендикулярную
проведем эти окружности. Начальные окружности касаются друг друга в полюсе Р. Через полюс Р проведем прямую, перпендикулярную  . Затем под углом
. Затем под углом  (для нормального зубчатого зацепления) проведем прямую N-N, на которую из центров
(для нормального зубчатого зацепления) проведем прямую N-N, на которую из центров 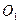 и
и  восстановим перпендикуляры
восстановим перпендикуляры 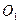 А и
А и  Р. Радиусами
Р. Радиусами 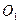 А и
А и  В проводим основные окружности. На отрезке АВ возьмем произвольную точку К.
В проводим основные окружности. На отрезке АВ возьмем произвольную точку К.
Если прямую N-N катать без скольжения по первой основной окружности, а затем по второй, то точка К опишет в начале эвольвенту 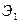 , а затем эвольвенту
, а затем эвольвенту 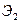 , которые примем за боковые профили зубьев зубчатых колес.
, которые примем за боковые профили зубьев зубчатых колес.
На основании свойства эвольвенты прямая N-N является одновременно нормалью эвольвент 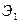 и
и 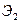 и, следовательно, должна проходить через точку их касания К. По-другому общая нормаль к эвольвентам не может пройти , так как должна касаться основных окружностей.
и, следовательно, должна проходить через точку их касания К. По-другому общая нормаль к эвольвентам не может пройти , так как должна касаться основных окружностей.
Линия N-N представляет собой геометрическое место точек касания зубьев и называется линией зацепления.
Вне этой линии зубья не контактируют. Прямая N-N не меняет своего положения и всегда пересекает межосевое расстояние  в полюсе Р. По основной теореме зацепления передаточное отношение для зубчатого механизма
в полюсе Р. По основной теореме зацепления передаточное отношение для зубчатого механизма 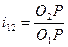 является постоянной величиной.
является постоянной величиной.
Установим границы линии зацепления. Участок АВ называется теоретической частью линии зацепления. Первой точкой зацепления колес будет точка а – точка пересечения окружности вершин 2 колеса с линией зацепления N-N. Последней будет находиться в зацеплении точка пересечения окружности вершин 1 колеса с линией зацепления.
Участок ab называется рабочий участок линии зацепления.
Дуги начальных окружностей между положениями соответствующих профилей зубьев в начале и конце зацепления для каждого из колес называются дугами зацепления.
Угол  называется углом зацепления.
называется углом зацепления.
Дата добавления: 2016-03-05; просмотров: 692;
