Использование теории ожидаемой полезности при принятии решений
Как показывает практика, люди далеко не всегда принимают решения исходя из реальных значений. Подсознательно они ориентируются на субъективную "ценность" исходов. Одним из первых, кто сформулировал это и предпринял попытку дать свое теоретическое объяснение, был математик Д. Бернулли. Изучая так называемый "петербургский парадокс", он еще в 1738 году предположил, что при сравнении альтернатив реальный человек ориентируется не на ожидаемое значение самого выигрыша, а на математическое ожидание его субъективной "полезности". Развивая данную идею, Бернулли ввел понятие функции полезности, предложил для нее формулу и описал свойства. Это послужило основой теории ожидаемой полезности, которая до сих пор применяется для объяснения поведения экономических агентов в условиях риска.
Функция полезности отражает меру психологического удовлетворения благами. Традиционно она обозначается u(x). Единицей измерения полезности является "ютил". Аргументом х для данной функции выступает количество благ. В наших примерах в качестве х используются денежные суммы выигрышей, прибыли или убытков. Поэтому u(x) представляет функцию полезности денег.
Согласно предположению Бернулли, альтернативы сравниваются по их ожидаемой полезности. Чтобы ее рассчитать, необходимо в соответствие каждому возможному исходу x поставить некоторое значение полезности u. Это можно сделать, введя функцию полезности u(x), определяющую однозначную зависимость между х и u.
Свойства данной функции:
1) функция полезности должна быть возрастающей. Это отражает принцип: "чем больше благ, тем лучше";
2) в общем случае, функция полезности должна быть непрерывна, поскольку если две альтернативы обеспечивают нам близкое количество благ, то и полезности этих двух альтернатив должна быть близкими.
3) функция полезности должна отражать отношение ЛПР к риску - склонность или неприятие. Это значит, что функция должна корректно описывать различия в психологическом восприятии ЛПР потерь и выигрышей.
В зависимости от отношения к риску выделяют три чистых психологических типа:
· не склонный к риску ("рискофоб");
· нейтральный к риску;
· склонный к риску ("рискофил").
Люди, относящиеся к указанным типам, по-разному оценивают потери и выигрыши. У лиц, не склонных к риску, психологические переживания в связи с потерей некоторой суммы денег являются более сильными, чем удовлетворение от выигрыша такой же суммы. Это означает, что для такого ЛПР, обладающего богатством в размере х0 рублей, функция полезности должна удовлетворять условию:
u(x0) - u(x0 - Δх) > u(x0 + Δх)- u(x0),
где: u(x0) - u(x0 - Δх) - отражает уменьшение полезности (то есть меру переживаний, неудовлетворения) из-за потери Δх рублей, u(x0 + Δх) - u(x0) - отражает увеличение полезности (то есть меру удовлетворения) от выигрыша такой же суммы Δх.
Данное условие выполняется, если функция полезности является "выпуклой вверх". На рис. 21 хорошо видно, что выпуклая вверх функция u(x) действительно отражает большую "чувствительность" ЛПР к возможным потерям, чем к выигрышам.
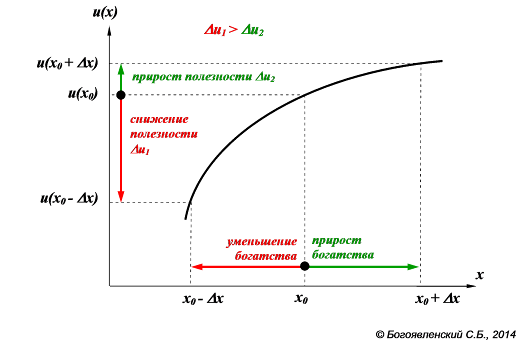
Рис. 21. Выпуклая ВВЕРХ функция полезности, отражающая НЕПРИЯТИЕ риска.
Напротив, для ЛПР, любящего рисковать, психологические выгоды от возможности выиграть Δх рублей превосходят переживания из-за такой же потери. Подобное отношение к риску описывается "выпуклой вниз" функцией полезности (рис. 22).
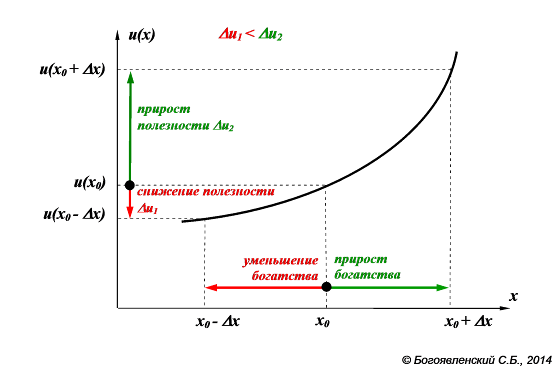
Рис. 22. Выпуклая ВНИЗ функция полезности, отражающая СКЛОННОСТЬ к риску.
Функция полезности для лиц, нейтральных к риску, представляет собой прямую (рис. 23), обеспечивая тем самым одинаковое (равное) отношение как к выигрышам, так и к проигрышам. Все рассмотренные нами в предыдущих главах методы принятия решений были справедливы именно для ЛПР, относящегося к такому типу поведения.
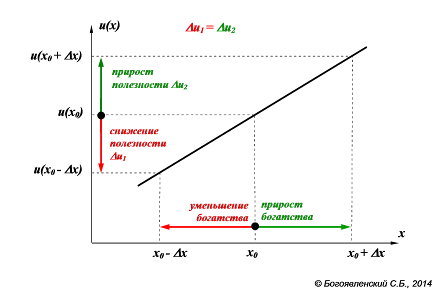
Рис. 23. Линейная функция полезности, отражающая НЕЙТРАЛЬНОЕ отношение к риску.
Итак, функция полезности в теории - это возрастающая непрерывная функция, выпуклая вверх для лиц, не склонных к риску, выпуклая вниз для тех, кто любит риск, и прямая для людей, нейтральных к риску.
Следует отметить, что перечисленные типы являются "чистыми". Люди, относящиеся исключительно к одному чистому типу, в жизни встречаются редко. В зависимости от возраста, ситуации, настроения, уровня богатства, величины возможных потерь или выигрышей один и тот же человек может демонстрировать как "рискофобное" поведение, так и склонность к риску, либо "нейтралитет".
Согласно исследованиям, основная часть людей в экономическом плане в большей или меньшей степени демонстрируют неприятие риска. Поэтому в экономической литературе значительное внимание уделено именно такому типу поведения.
Чтобы выявить специфику экономического поведения в условиях риска мы будем использовать модель так называемой "простой лотереи" или "простого шанса". У ЛПР есть шанс оказаться в состоянии х1 с вероятностью р1 = р и в состоянии х2 с вероятностью р2 = (1 - р). Других возможностей, кроме этих двух вариантов, нет. Поэтому такую лотерею также часто называют бинарной. В кратком виде "простой шанс" записывается следующим образом:
L = { x1, x2, p}
Ожидаемый результат такой лотереи ML может быть определен по общей формуле для расчета математического ожидания дискретной СВ:
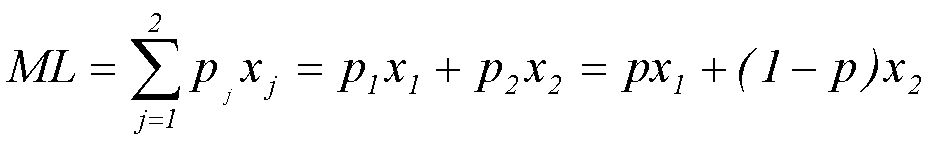
Ожидаемая полезность данной лотереи MuL рассчитывается по аналогичной формуле, только вместо реальных значений исходов х1 и х2 в нее подставляются значения функции полезности u(х1) и u(х2):
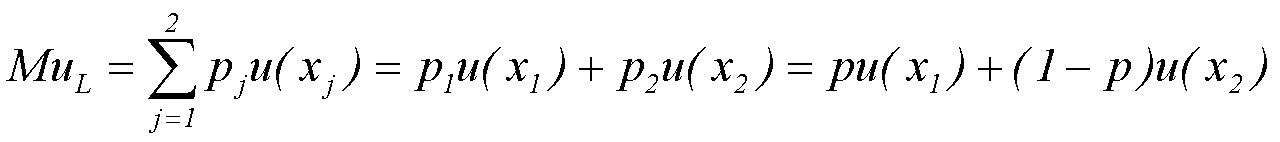
Это означает, что на координатной плоскости ожидаемая полезность будет находиться на отрезке, соединяющем значения функции полезности u(х1) и u(х2) (рис. 24), причем:
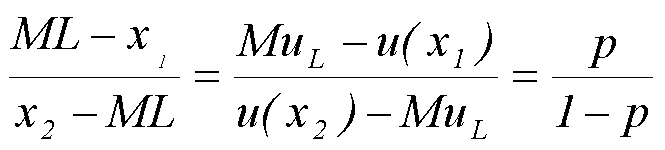
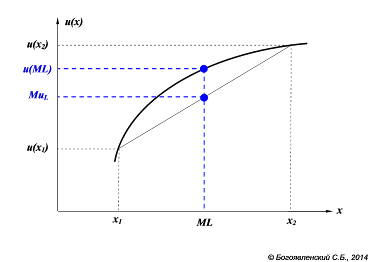
Рис. 24. Сравнение рисковой и безрисковой альтернатив для ЛПР, несклонного к риску.
Опираясь на график, попробуем понять, как люди, по-разному относящиеся к риску, ответили бы на два простых вопроса.
Вопрос 1. Что лучше: гарантированно иметь некоторую сумму денег или получить возможность сыграть в лотерею, ожидаемый выигрыш в которой равен этой же сумме? Вариант с гарантированным обладанием деньгами называется "безрисковая альтернатива" (sure alternative). В свою очередь, возможность сыграть в лотерею по аналогии называют "рисковой альтернативой". Из графика полезности ЛПР, не склонного к риску (рис. 24), видно, что ожидаемая полезность лотереи MuL при любых значениях х1, х2 и р будет ниже полезности гарантированной суммы в размере ожидаемого выигрыша ML: u(ML) > MuL Это означает, что осторожные люди, не любящие риск, предпочтут получить гарантированную сумму вместо того, чтобы сыграть в лотерею с таким же ожидаемым выигрышем. Нетрудно показать, что лица, склонные к риску, в подобных условиях выберут лотерею, а для "нейтрала" рисковая и безрисковая альтернативы будут равноценны.
Вопрос 2. Какая игра лучше: игра, где можно много выиграть, но и много проиграть, или где возможный выигрыш меньше, но проигрыш незначительный? Для ответа на этот вопрос рассмотрим две простые лотереи L{x1, x2, p} и L'{x'1, x'2, p'}, такие что: x1 < x'1 и x'2 < x2
Лотерея L дает возможность выиграть больше, чем L', но и возможный проигрыш здесь тяжелее. Исходы лотереи L' не выходят за пределы L. Относительно вероятностей выигрыша или проигрыша никаких предположений не вводим. Как мы увидим дальше, ответ на интересующий нас вопрос в данном случае от вероятностей не зависит. Как уже отмечалось выше, ожидаемая полезность каждой из этих лотерей лежит на хорде, которая соединяет две точки на графике полезности, соответствующие двум возможным исходам. Точное положение ожидаемой полезности на этой хорде зависит от вероятности выиграть или проиграть. Проводя все возможные хорды для любых значений х1, х2 , х'1 , х'2 при условии, что x1 < x'1 и x'2 < x2 (рис. 25), можно заметить следующую закономерность. При выпуклом вверх графике полезности хорда, описывающая ожидаемую полезность второй лотереи L', всегда выше хорды для L. Это означает, что при заданных пределах ЛПР, не склонный к риску, всегда будет выбирать альтернативу с меньшим разбросом исходов.
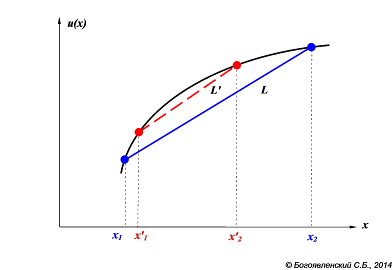
Рис. 25. Влияние разброса исходов простой лотереи на ожидаемую полезность альтернатив для ЛПР, несклонного к риску.
Лицам, хорошо воспринимающим риск, а, значит, и менее чувствительным к возможным проигрышам, вариант с широким диапазоном исходов (а, значит, и с более значительным выигрышем) кажется привлекательней.
При нейтральном отношении к риску решение будет зависеть не от разброса исходов, а от ожидаемого значения. Здесь может оказаться предпочтительным вариант с широким разбросом, если он обещает больший ожидаемый выигрыш (и, следовательно, более высокую ожидаемую полезность).
Как было указано выше, мы разделили людей в зависимости от их отношения к риску на три типа: рискофобы, рискофилы и нейтралы. Но на принятие решения влияет не только общая направленность, но и степень толерантности к риску. Действительно, два рискофоба в одинаковых ситуациях могут выбрать разные альтернативы, потому что их "сила отторжения" риска различна. Что же может служить мерой неприятия риска? По каким показателям можно судить, насколько человек толерантен к риску? Мы отметили готовность человека, не склонного к риску, платить за его отсутствие. Это дает возможность использовать количественные характеристики такой готовности в качестве меры неприятия риска. Действительно, чем сильнее человек опасается риска, тем больше он согласен заплатить за его отсутствие. Эта готовность платить (willingness to pay) может быть количественно измерена, как минимум, двумя показателями:
· величиной максимальной страховой премии, на которую согласен ЛПР;
· величиной так называемой "премии за риск".
Премия за риск может быть представлена как в абсолютных, так и в относительных величинах (как доля от максимальной страховой премии). Рассмотрим эти характеристики подробнее на примере гипотетической ситуации с человеком, не склонным к риску и обладающим начальным богатством х0 денежных единиц.
Предположим, что с вероятностью р может произойти убыток в размере у денежных единиц. Дискретная случайная величина Y, описывающая данный убыток, может быть записана как простейшая лотерея Y {y, 0, p}. Начальное богатство детерминировано и равно х0. Но поскольку убыток случаен, то конечное богатство также является случайной величиной Х:
Х = x0 - Y
Распределение этой случайной величины имеет следующий вид:
• с вероятностью р конечное богатство равно (х0 - у), а
• с вероятностью (1 - р) оно останется неизменным и равным х0.
Данная схема описывает типичную ситуацию так называемого "чистого" риска, который несет в себе возможность только потерять и не предполагает возможность обогатиться. В лучшем случае все просто останется, как есть.
График полезности для рассматриваемой ситуации приведен на рис. 26.
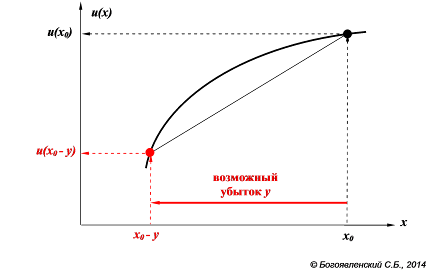
Рис. 26. Полезность возможных исходов конечного богатства.
Ожидаемое конечное богатство МХ составляет:
MX = M(x0 - Y) = M(x0) - MY , где
MY - ожидаемый убыток, который может быть найден по общей формуле математического ожидания для дискретной СВ:
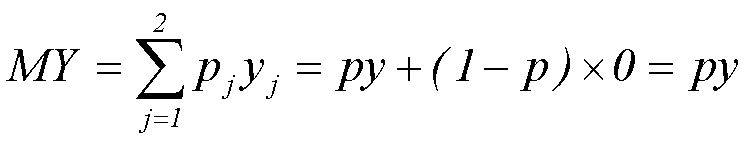
Так как x0 - детерминированная величина, то ее математическое ожидание равно самому значению: M(x0) = x0. Таким образом: MX = x0 - MY
Поскольку мы рассматриваем ситуацию с позиции ЛПР, не склонного к риску, то ожидаемая полезность конечного богатства MuX оказывается меньше полезности ожидаемого конечного богатства u(MX) (рис. 27). Значит ЛПР хотел бы избавиться от риска, даже если за это он должен заплатить некоторую сумму.

Рис. 27. Полезность ожидаемого конечного богатства u(MX) и ожидаемая полезность конечного богатства MuX.
Объективная составляющая, равная ожидаемому убытку MY, представляет собой "чистую" цену риска. Она определяется только вероятностью и тяжестью убытков и не зависит от отношения ЛПР к риску. Ожидаемый убыток MY одинаков как для рискофоба, так и для нейтрала, либо рискофила, поскольку он рассчитывается исходя из характеристик самого риска и не связан с функцией полезности.
Субъективная составляющая, напротив, зависит не только от объективных параметров риска, но и субъективного отношения ЛПР к риску, которое определяет форму функции полезности. Эту составляющую π называют "премия за риск" (risk premium) или "премия за безопасность" (safety premium). От чего же зависит ее величина?
Во-первых, премия за риск зависит от размеров начального богатства. Еще Бернулли предположил, что полезность изменяется пропорционально относительному, а не абсолютному приращению капитала. Если это допущение справедливо, то, чем больше начальное богатство х0, тем слабее влияет убыток y на изменение ожидаемой полезности. Значит, рисковая премия π для больших уровней богатства будет ниже, чем для маленьких.
Во-вторых, рисковая премия зависит от разброса убытка относительно ожидаемого значения. Это интуитивно понятно - чем шире рассеивание, тем больший убыток можно получить. Следовательно, рисковая премия будет больше.
Третий фактор, влияющий на величину рисковой премии - степень неприятия риска. Это также логически объяснимо: чем меньше человек склонен к риску, тем больше он готов заплатить за страхование. На графике "повышенное" неприятие риска выражается большей кривизной (выпуклостью) функции полезности. Данный фактор является наиболее субъективным из всех рассмотренных. Именно он объясняет, почему два рискофоба, находясь в одинаковых условиях, могут выбрать разные альтернативы. Просто один из них в большей степени не приемлет риск, чем второй. Поэтому у него выше готовность платить за риск (в частности, больше рисковая премия).
Теория ожидаемой полезности действительно объясняет многие феномены поведения человека в ситуации риска и может использоваться при принятии решений. Но существенной проблемой является то, что для конкретного ЛПР функция полезности неизвестна! Поскольку она описывает степень психологического удовлетворения благами данного лица, для ее построения невозможно использовать только объективные оценки. В любом случае она базируется на субъективных оценках, которые могут быть получены только путем опросов, анкетирования или анализа поведения разных людей в схожих рисковых ситуациях. Но не существует двух абсолютно одинаковых людей и полностью идентичных условий. Кроме того, выбор в искусственно предложенных при анкетировании обстоятельствах может существенно отличаться от решения, который этот же человек примет в схожих, но реальных условиях! Поэтому точное построение функции полезности весьма проблематично. Тем не менее, это можно пытаться сделать, и ниже мы рассмотрим один из подходов к решению данной задачи.
Функцию полезности можно построить по точкам. Каждое значение получается в результате обработки ответа ЛПР на вопрос о выборе одной из двух альтернатив. Одна - рисковая, другая - детерминированная. В результате ответа необходимо оценить, при каких параметрах эти две альтернативы будут с точки зрения ЛПР равноценны. Тогда, исходя из равенства их ожидаемых полезностей, можно оценить значение функции полезности для заданного значения богатства. Чтобы было более понятно, рассмотрим пример.
Человеку предлагается ответить на следующий вопрос анкеты:
У Вас есть всего 100 тыс. руб. и две возможности...
(А) инвестировать их в паевой фонд на один год и получить через год с вероятностью 50/50 либо 500 тыс.руб., либо 50 тыс.руб.
(В) положить их на депозит в банк, и через год гарантированно получить с процентами S руб. Какова должна быть величина S, чтобы альтернативы (А) и (В) были для Вас равноценны?
Формально, ЛПР, обладающему начальным богатством х0=100 т.р., предлагается выбрать из двух альтернатив:
· рисковая А представляет собой простую лотерею А{50, 500, 0.5};
· безрисковая В гарантированно обещает S т.р.
Рассмотрим альтернативу А. Ее ожидаемый исход может быть рассчитан по общей формуле математического ожидания:
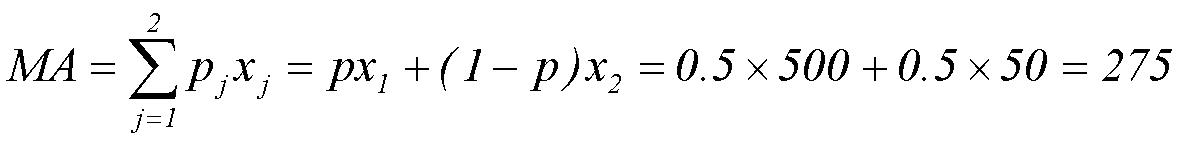 (т.р.)
(т.р.)
Ожидаемая полезность альтернативы А равна:
MuA = p u(x1) + (1-p) u(x2) = 0.5 u(50) + 0.5 u(500)
Самой функции полезности u(x) мы не знаем. Но нам известны некоторые ее свойства, например, то, что она возрастающая. Другим важным свойством, еще не упоминавшимся, является ее "нечувствительность" к линейным преобразованиям. Напомним, что линейные преобразования включают возможность прибавить или вычесть постоянные значения, а также умножить или разделить на постоянную величину, отличную от нуля. Пусть функция u(x) получена путем линейных преобразований из функции g(x) :
u(x) = c1 g(x) + c2, где c1, c2 - const, c1 ≠ 0
Тогда, благодаря свойству функции полезности u(x) будет описывать ту же систему предпочтений, что и g(x). Для сравнения альтернатив важны не абсолютные значения полезности, а то, как они соотносятся между собой. Если до преобразования выполнялось неравенство:
g(x1) > g(x2),
то после линейных преобразований порядок сохранится, и полезность исхода х1 по-прежнему будет выше полезности исхода х2:
U(x1) > u(x2).
Это свойство позволяет нам принять за ноль значение функции полезности для любого конкретного значения х и установить любое единичное деление для измерения полезности. Поэтому, чтобы было проще строить u(x), примем:
u(50) = 0
u(500) = 1
Значит, нам известны две точки, через которые проходит график искомой функции полезности u(x): О1(50, 0) и О2(500, 1) (см. рис. 28).
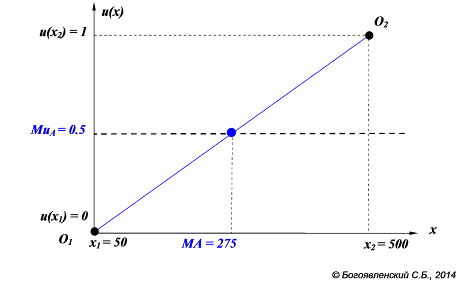
Рис. 28. Ожидаемая полезность рисковой альтернативы А.
Ожидаемая полезность альтернативы А при таком нормировании функции полезности будет равна 0.5:
MuA = 0.5 u(50) + 0.5 u(500) = 0.5 × 0 + 0.5 × 1 = 0.5
Чтобы альтернативы А и В были равноценны, их ожидаемые полезности должны быть равны: MuA = MuB
Ожидаемая полезность альтернативы В равна полезности гарантированной суммы S, так как она детерминирована: MuB = u(S)
Тогда u(S) = MuА = 0.5
То есть график u(x) должен проходить через точку с координатами (S, MuА), в нашем случае (S, 0.5) (рис. 29).
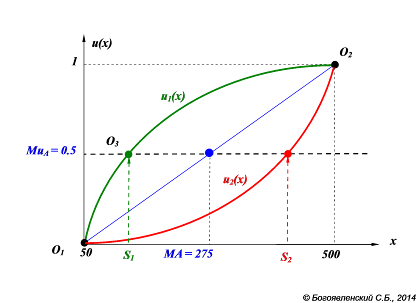
Рис. 29. Ожидаемая полезность безрисковой альтернативы В.
В зависимости от того, какую сумму S назвал ЛПР при ответе на вопрос анкеты, график может оказаться выпуклым как вверх, так и вниз.
Если названная ЛПР сумма S1 будет меньше ожидаемого исхода рисковой альтернативы S1 < MA, это означает, что человек предпочитает пусть и меньший, но гарантированный выигрыш, негативно относится к риску, и его функция полезности имеет выпуклый вверх график.
Если же выбранная ЛПР сумма больше ожидаемого выигрыша, S2 > MA, значит, мы имеем дело с лицом, склонным к риску и готовым поучаствовать в лотерее. Его привлекает шанс получить выигрыш и не очень пугает возможность потерять часть средств. Для такого человека функция полезности будет выпуклая вниз.
В любом случае у нас уже есть три точки, через которые проходит график u(x): О1(50, 0), О2(S, 0.5), О3(500, 1). Мы можем построить его хотя бы приблизительно.
Обычно при анкетировании задают несколько вопросов с разными альтернативами и/или сочетаниями параметров x0, x1, x2, p. Это позволяет строить график по большему количеству точек, что повышает его точность. Однако, к сожалению, приходится признать, что надежность таких оценок не высока.
Дата добавления: 2016-03-04; просмотров: 2797;
