Неметрическое многомерное шкалирование

10.3 Различные варианты неметрического многомерного шкалирования были предложены Р.Шепардом, Д.Краскелом и Л.Гуттманом. Обычно используются методы двух последних авторов.

В методах многомерного шкалирования используется мера близости между эмпирическими и визуальными расстояниями, показывающая насколько хорошо вторые соответствуют первым. На практике чаще используется характеристики так называемого стресса, введенные Д.Краскелом или коэффициент отчуждения Л.Гуттмана. Поясним конструкции этих показателей.

По смыслу неметрического многомерного шкалирования между эмпирическими D_ij и визуальными v_ij расстояниями должны наблюдаться такие соотношения, что монотонной последовательности первых из них

D_ij < D_lt < D_pq (9.6)

должна соответствовать также монотонная последовательность - вторых

v_ij < v_lt < v_pq . (9.7)

Пусть для некоторой полученной конфигурации соотношения величин D_ij и v_ij таково, как это представлено на рисунке 10.1. Видно, что упорядоченность значений D_ij не со-провождается точной монотонной упорядоченностью визуальных расстояний v_ij, и име-

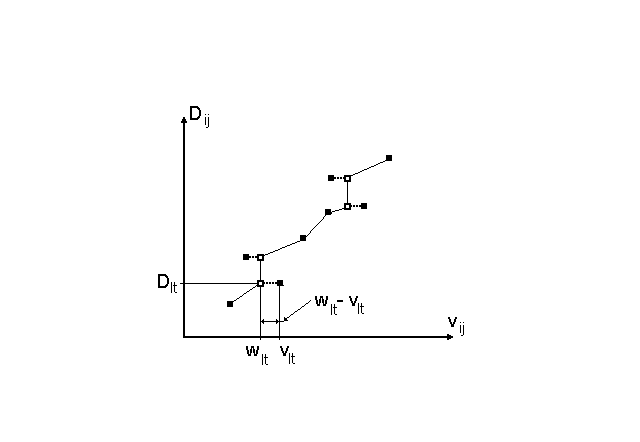
Рисунок 10.1. К понятию отклонения w_ij для визуального расстояния v_ij, соответствующего эмпирическому расстоянию D_ij

- 257 -

ются случаи, когда она нарушена. Для каждого из таких случаев нарушений соответствия неравенств (9.6) и (9.7) можно ввести понятие так называемого отклонения w_ij. Величина w_ij есть такое идеализированное значение v_ij, соответствующее D_ij, для которого нарушения монотонности и соответствия двух неравенств не наблюдается. Иными словами, все значения отклонений w_ij для эмпирических расстояний D_ij должны располагаться на монотонной ломаной линии (рис.10.1). Тогда неравенству (9.6) будет соответствовать выполнение менее строгого неравенства для значений отклонений

w_ij £ w_lt £ w_pq . (9.8)

Очевидно, чем ближе будут значения визуальных расстояний и соответствующих им отклонений и чем меньше будут значения их разностей w_ij - v_ij, тем более точно будет соблюдаться соответствие неравенств (9.6) и (9.7), и тем лучше будут результаты неметрического многомерного шкалирования.

10.4 Для описания качества этих результатов Д.Краскел предложил использовать два показателя стресса, первый из которых находится по формуле

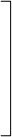
_{k k} ^1/2

S S (w_ij - v_ij)²

^{i = 1 j = 1}

S₁ = , (9.9)

_{k k}

S S v_ij²

^{i = 1 j = 1}

второй – из

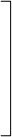
_{k k} ^1/2

S S (w_ij - v_ij)²

^{i = 1 j = 1}

S₂ = , (9.10)

_{k k}

S S (v_ij - M_v)²

^{i = 1 j = 1}

В формуле (9.10) M_v - средняя величина визуальных расстояний, для всей матрицы V. Нетрудно видеть, что обе формулы стресса основаны на сумме квадратов разностей отклонений и визуальных расстояний w_ij - v _ij . Чем меньше будет эта сумма, тем лучше окажутся результаты многомерного шкалирования. В ситуации, когда все эти разности будут равны нулю, последовательности эмпирических расстояний (9.6) будет соответствовать монотонная последовательность визуальных расстояний. Разница этих двух формул заключается в нормирующей величине, стоящей в знаменателе каждой из них. Существуют также формулы так называемого S-стресса, аналогичные выражениям (9.9) и (9.10), но в которых вместо значений w _ij и v _ij используются их квадраты w_ij² и v _ij².

Иной способ измерения близости визуальных расстояний и отклонений используется в методе многомерного шкалирования, разработанном Л.Гуттманом. Здесь применяется так называемый коэффициент монотонности

- 258 -

_{k k}

S S w _ij v _ij²

^{i = 1 j = 1}

m = , (9.11)

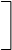
_{k k k k} ^1/2

S S w _ij² S S v _ij²

^{i = 1 j = 1 i = 1 j = 1}

который является корреляционной мерой согласованности значений w_ij и v_ij. На его основе находится коэффициент отчужденности или алиенации

K = (1 - m²)^1/2 , (9.12)

значение которого будет тем меньше, чем лучше соответствие между визуальными расстояниями и отклонениями.

Значения стресса или коэффициента отчужденности служат ориентиром для поиска наилучшей конфигурации неметрического многомерного шкалирования. Вычислительные процедуры построены так, чтобы в ходе итерационного процесса получалась такая матрица конфигурации X, которой соответствовала бы минимальная величина стресса. На каждой из этих итераций в ходе достаточно сложно организованных вычислений находится X, по которой определяется матрица визуальных расстояний V, с вычислением по ней значения стресса S или коэффициента отчужденности K. Величины S или K сравниваются со значениями этих показателей, найденными на предыдущей итерации. Если они уменьшились, проводится следующая итерация, в ходе которой качество конфигурации многомерного шкалирования улучшается. Если уменьшения значений S и K не произошло, считается, что достигнут их минимум, и тем самым получена наилучшая конфигурация. По ней строиться график неметрического многомерного шкалирования.

С деталями алгоритмов итерационного вычислительного процесса неметрического многомерного шкалирования можно познакомиться по книгам А.Ю.Терехиной (1986) и М.Дэйвисона (1988).

10.5Для оценки качества полученной конфигурации и соответствующего ей графика используется финальная величина стресса S_o или коэффициента отчужденности K_o, полученные как наименьшие достигнутые их значения. Обычно приемлемой считается величина стресса не превышающая уровня 0.10, т.е. - S_o £ 0.10.

По финальной величине стресса можно опытным путем определить необходимую размерность конфигурации, то есть – число осей графика многомерного шкалирования X_i. Дело в том, что до начала вычислений требуется задать эту размерность. Обычно стремятся получить максимально наглядный результат, чему соответствуют две или три его оси X_i. Чаще всего пытаются получить двумерный график как наиболее наглядный. При реализации процедуры одним из ее результатов является финальная величина стресса S_o. Если она не превышает критического порога в 0.10, то многомерное шкалирование считается успешным. Тогда можно думать, что на двумерном графике мы увидим взаиморасположение точек, хорошо соответствующее реальным значениям эмпирических расстояний между представляемыми этими точками исследуемыми единицами. Однако, если S_o заметно превышает этот порог, многомерное шкалирование на плоскость считается неудачным. Тогда можно попытаться улучшить его результаты, что обычно достигается

- 259 -

при увеличении на одну ось размерности конфигурации. Повторение многомерного шкалирования для трех осей X_i часто может уменьшить финальную величину стресса, так что условие S_o £ 0.10 станет выполняться. Это позволит считать повторные результаты удачными.

Возможна и обратная ситуация, когда финальная величина стресса окажется малой, то есть меньшей уровня 0.05. В этом случае можно попытаться повторно получить результат для многомерного шкалирования с уменьшенным на единицу числом осей X_i. Так, если при первом шкалировании были заданы 3 оси, можно попытаться получить плоский двумерный график. Разумеется, при повторном шкалировании для финального стресса должно выполняться условие S_o £ 0.10.

10.6 Другим важным результатом, позволяющим контролировать качество проведенного многомерного шкалирования, является так называемая диаграмма Шепарда. Она представляет собой график обычного корреляционного поля (рис.10.2), где на одной из осей откладываются значения эмпирических расстояний D_ij, на другой - величины визу- альных расстояний v_ij. Эта диаграмма позволяет наглядно судить о том, как хорошо видимые на графике многомерного шкалирования значения v_ij соответствуют расстояниям D_ij.

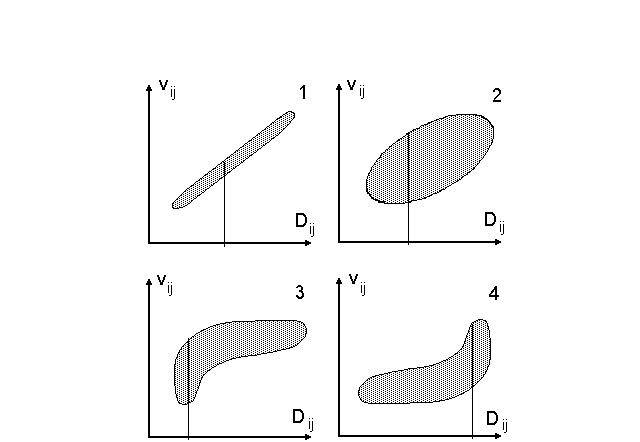
Рисунок 10.2. Вид диаграммы Шепарда для разных результатов многомерного шкалирования. Обозначения: 1 – удачный результат, 2 - 4 - неудачные результаты

- 260 -

В ситуации удачного многомерного шкалирования на диаграмме Шепарда представлено вытянутое узкое и примерно прямолинейное корреляционное поле (рис.10.2, случай 1). В этом случае можно считать, что значения v_ij в среднем примерно пропорциональны соответствующим эмпирическим расстояниям D_ij, а отклонения от этой пропорциональности - невелики. Сильно размытое корреляционное поле (рис.10.2, случай 2) свидетельствует о плохих результатах многомерного шкалирования, когда какое-то значение визуального расстояния v_ij может соответствовать самым разным ( большим и малым) величинам D_ij. Криволинейный характер корреляционного поля на диаграмме Шепарда (рис.10.2, случаи 3 и 4) также свидетельствует о неудачном многомерном шкалировании. В этих ситуациях малым или большим значениям визуальных расстояний v_ij будет соответствовать почти весь спектр величин эмпирических расстояний D_ij.

10.7 Существуют определенные практические проблемы, которые следует учитывать при проведении неметрического многомерного шкалирования. Одной из них является вопрос об исходной конфигурации, которая в дальнейшем подвергается итерационному улучшению. Существуют разные способы ее задания. Наиболее распространен случай, когда в качестве исходных применяются результаты проведения метрического шкалирования, сходного с методом Торгенсона. Компьютерные программы анализа данных обычно по умолчанию используют этот способ.

Возможно также применение в качестве исходного приближения конфигурации результатов предыдущего неметрического шкалирования, проведенного для этой же самой матрицы эмпирических расстояний. Тогда все вычисления осуществляются в два этапа. На первом из них проводится неметрическое многомерное шкалирование при задании его размерности на одну единицу превышающей ту, которая кажется обоснованной или желательной. Полученные результаты в дальнейшем используются в качестве первоначальной конфигурации для второго этапа вычислений, когда задается уже желательная размерность.

Вторым практическим аспектом неметрического шкалирования, который также следует учитывать, является необходимость выполнения достаточного числа итераций, в ходе которых улучшается конфигурация и уменьшается величина стресса. Обычно, при реализации этих вычислений в компьютерных программах анализа данных по умолчанию задается предельное количество в 50 итераций. Иногда этого их количества бывает недостаточно, и минимальный стресс остается не достигнутым. Для избежания получения такого результата следует задавать 150-200 итераций, что обычно в большей степени гарантирует достижение сходимости вычислительного процесса.

Пример 10.1 Проведем неметрическое многомерное шкалирование матрицы таксономических расстояний, которая подвергалась иерархическому агломеративному кластерному анализу в примере 9.1. Для проведения вычислений была задана размерность конфигурации равная 2, чему должен соответствовать плоский график, опирающийся на две оси X₁ и X₂. В качестве метода получения стартовой конфигурации был задан способ предварительного проведения метрического шкалирования. При проведении 33 итераций были достигнуты финальные значения стресса S_o = 0.122 и коэффициента алиенации K_o = 0.149. Так как величина S_o весьма близка к критическому значению 0.10,

- 261 -

результаты шкалирования можно считать относительно удачными. Об этом же свидетельствует и диаграмма Шепарда (рис.10.3), на которой видно, что связь визуальных и эмпирических расстояний достаточно тесна, а корреляционное поле характеризуется прямолинейностью. Это означает, что те точки на графике, которые мы увидим близко расположенными друг от друга, характеризуются малыми эмпирическими расстояниями. Напротив, для точек, расположенных на графике далеко друг от друга, расстояния D_ij будут большими. График неметрического многомерного шкалирования, соответствующий полученной конфигурации приведен на рисунке 10.4.

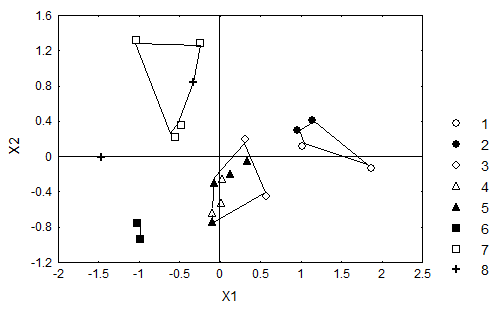
При его рассмотрении можно обнаружить заметное сходство взаимного расположения точек с теми результатами, которые были найдены нами при проведении иерархического кластерного анализа. Действительно, северо-западные и северные коми обнаруживают компактное облако близко расположенных точек. В этом облаке выборка удорских коми до некоторой степени обособлена от остальных трех групп. Западные, восточные и южные коми также образуют на графике достаточно компактный и обособленный кластер. Иньвенские коми-пермяки и велвинская группа язьвинских коми-пермяков также обнаруживают заметное взаимное сходство. Зюздинские коми-пермяки заметно отличны от остальных групп коми-пермяков и сближаются до некоторой степени с кластером, объединяющим западных, южных и восточных коми. Архангельская группа язьвинских коми-пермяков занимает обособленное положение и может быть с одинаковым основанием отнесена как к зюздинскому кластеру, так и к иньвенскому объединению, что не соответствует результатам кластерного анализа, когда эта группа отчетливо входила в один кластер с зюздинскими выборками.

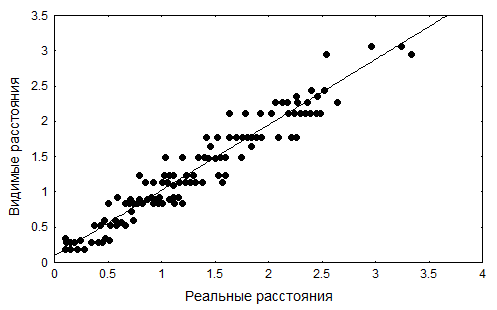
Рисунок 10.3. Диаграмма Шепарда результатов неметрического многомерного шкалирования 21 выборки коми и коми-пермяков

Рисунок 10.4. Результаты многомерного шкалирования 21 выборки коми и коми-пермяков

Пример 10.2 Проведем многомерное шкалирование материалов по размерам нейрокраниума ископаемых гоминид, принадлежащих видам: Homo erectus, Homo sapiens neanderthalensis и Homo sapiens sapiens из примера 8.4, где эти же данные подвергались каноническому анализу. Для набора 10 размеров нейрокраниума (табл.8.6) была найдена матрица расстояний Махаланобиса между отдельными наблюдениями, которая затем подвергалась многомерному шкалированию. Была задана размерность конфигурации равная 2, чему должен соответствовать график, опирающийся на две оси X₁ и X₂. В качестве метода получения стартовой конфигурации был задан способ предварительного проведения метрического шкалирования.

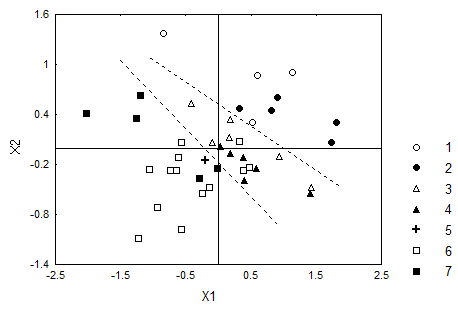
При проведении вычислительного процесса на 11 итерации была получена финальная величина стресса S_o = 0.086 < 0.10, что свидетельствует об удачности многомерного шкалирования. При рассмотрении графика конфигурации можно заметить, что взаимное расположение точек практически идентично той картине, которую можно было наблюдать по результатам канонического анализа (рис.8.5). По результатам многомерного шкалирования вся зона графика легко может быть разделена двумя граничными линиями на три участка. Первый из них включает неоантропов верхнего палеолита. Кафзех VI также размещается в этом участке графика, что соответствует сапиентной морфологии его нейрокраниума. Противоположный участок графика включает типичных представителей Homo erectus (Питекантроп I, Синантропы III, X, XII). Здесь же размещаются явантропы (Нгандонг V, XI) и так называемые пренеандертальцы (Брокен-Хилл, Салданья и Петралона). В средней зоне графика размещаются европейские, переднеазиатские и северо-африканские палеоантропы.

Таким образом, многомерное шкалирование дало те же самые результаты, что и канонический анализ. Индивидуальные оценки элементов конфигурации и значения двух кано

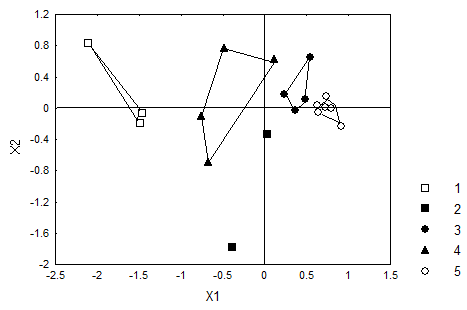
Рисунок 10.5. Результаты многомерного шкалирования вариантов нейрокраниума ископаемых гоминид.Обозначения: 1 – Homo erectus, 2 - пренеандертальцы, 3 - классические неандертальцы Европы, 4 - неандертальцы Передней Азии и Северной Африки, 5 - Кафзех VI, 6 - верхний палеолит Европы, 7 – верхний палеолит Азии и Африки

нических переменных очень тесно скоррелированы. Так, первая ось многомерного шкалирования и первая каноническая переменная имеют коэффициент корреляции, равный 0.999, для второй оси и второй канонической переменной соответствующий коэффициент корреляции также очень велик 0.990.

В примере 8.5 эти же самые данные были проанализированы с применением компонентного анализа, результаты которого достаточно отличались от тех, которые были найдены путем выделения канонических переменных. Проведенное многомерное шкалирование доказало, что именно главные компоненты привнесли в данные некоторые артефакты.

10.8 Рассмотрим как соотносится многомерное шкалирование с другими методами анализа данных. На первый взгляд наибольшее логическое сходство многомерного шкалирования можно найти по сравнению с кластерным анализом. Действительно, оба этих подхода используют в качестве исходного материала одну и ту же матрицу, описывающую близость между исследуемыми единицами.

Достоинством кластерного анализа на первый взгляд является то, что он может дать окончательную картину, отражающую структуру исследуемых единиц - например, выделить несколько систем кластеров, находящихся в определенных иерархических взаимоотношениях друг с другом. Однако, жесткая нацеленность кластерного анализа на получение окончательного результата в некоторых случаях может приводить к нежелательным последствиям.

- 264 -

Во-первых, кластерный анализ предназначен для выделения обособленных кластеров независимо от того, имеются ли они в рассматриваемых данных. Иными словами, до применения этого метода всегда следует знать, что структура данных - дискретна. В противном случае, например, в ситуации непрерывной унимодальной вариации, выделенные кластеры могут оказаться фиктивными и описывающими чисто случайные явления. Аналогичная ситуация возникнет в случае существования в изучаемой вариации не дискретных вариантов, а - клин с непрерывными градиентами.

Во-вторых, кластерный анализ плохо учитывает возможную промежуточность некоторых из рассматриваемых единиц, которые, например, могут объективно находиться примерно на разном расстоянии от двух действительно существующих кластеров. Тогда кластеризация, опираясь на несколько большую близость (часто имеющую к тому же случайный характер) промежуточных единиц к тому или иному кластеру, жестко расклассифицирует их, а эта реально существующая промежуточность никак не будет отражена на дендрограмме. С таким случаем мы сталкивались при рассмотрении примеров 9.1 и 10.1. Параллельное применение трех иерархических агломеративных процедур выявило вхождение архангельской группы язьвинских коми-пермяков в один кластер с зюздинским выборками. Однако, неметрическое шкалирование продемонстрировало специфический и во многом промежуточный характер этой группы.

Результаты многомерного шкалирования лишены жесткой нацеленности на окончательное выявление кластеров с точностью до самой последней рассматриваемой единицы. Они просто предоставляют исследователю наглядную картину взаимного расположения всех объектов в соответствии с их эмпирическими расстояниями. Поэтому, многомерное шкалирование лишено описанных недостатков кластеризации. Действительно, если структура данных характеризуется непрерывным характером, то исследователь увидит соответствующую картину, лишенную дискретной структуры. В ситуации, когда некоторые выборки будут по своему статусу промежуточными между какими-то антропологическими общностями, на графике многомерного шкалирования эту промежуточность можно будет увидеть наглядно.

Определенное сходство можно найти и между каноническим анализом и многомерным шкалированием. Оба этих метода обладают возможностями визуализации данных - наглядного представления в графическом виде взаимоотношений между рассматриваемыми единицами. Однако, если многомерное шкалирование представляет всю изучаемую вариацию, то канонический анализ - лишь наиболее важную ее часть, соответствующую важнейшим закономерностям межгрупповой вариации. С другой стороны, значения канонических переменных как дискриминантных функций проградуированы в долях внутригруппового среднего квадратического отклонения, что позволяет легко оценивать величину межгрупповых различий. Многомерное шкалирование этого полезного свойства лишено.

Справедливости ради следует отметить и недостаток многомерного шкалирования. Оно требует проведения весьма сложных вычислений, и в стандартных пакетах программ обычно невозможно одновременно рассматривать более чем несколько десятков единиц. Канонический анализ, однако, может включать сотни и даже тысячи выборок.

Многомерное шкалирование может также применяться и для анализа корреляционных матриц, описывающих взаимосвязи признаков. В результате можно в наглядном ви-

Рисунок 10.6. Результаты многомерного шкалирования 21 размера тела по выборке 242 женщин. Обозначения: 1 - длины корпуса, ноги и руки, 2 - плечевой и тазовый диаметры, 3 - обхваты корпуса и конечностей, 4 – диаметры мыщелков сегментов конечностей, 5 - жировые складки.

де представить взаимное расположение точек, в соответствии их коэффициентами корреляции. В этом случае по существу решается одна из задач факторного анализа - группировка признаков.

Пример 10.3 Рассмотрим использование неметрического многомерного шкалирования к наглядному представлению признаков в соответствии с их взаимными корреляциями. Использовалась выборка 242 женщин, которая ранее нами рассматривалась при проведении факторного анализа в примерах 6.1 - 6.5. Анализу подвергалась корреляционная матрица 21 размера тела. Задавалась размерность шкалирования на две оси.

На 19-й итерации вычислений была получена финальная величина стресса S_o = 0.114. Она весьма незначительно превышает пороговый уровень 0.10 и результаты многомерного шкалирования на плоский график можно считать приемлемыми. Как это видно из рисунка 10.6, по полученным результатам можно осуществить отчетливую группировку размеров тела.

Одна из выделившихся групп признаков, образована продольными размерами скелета корпуса и конечностей. Длины ноги и руки связаны высокими корреляциями и на графике располагаются в непосредственной близости. Длина корпуса до некоторой степени обособлена от них. Другой полюс на графике составляют объединения жировых складок и обхватов корпуса и конечностей, зависящих в своем развитии от мягких тканей. Обе эти группы признаков расположены в непосредственной близости. К ним тяготеет тазовый диаметр, который у женщин в значительной степени зависит от подкожного жироотложения. Акромиальный диаметр обособлен как от обхватов и жировых скла-

- 266 -

док, так и от продольных размеров тела. Костные диаметры, ориентированные на мыщелки конечностей, занимают промежуточное положение между объединениями обхватов и жировых складок, с одной стороны и продольными размерами тела, но несколько ближе - к первым. Последнее обстоятельство может быть связано с тем, что диаметры локтя и колена у женщин также включают заметный подкожный жировой компонент.

10.9 С методами многомерного шкалирования можно познакомится по книгам А.Ю.Терехиной (1986) и М.Дэйвисона (1988). Метрическое многомерное шкалирование изложено в работе У.Торгерсона (1972).