Многомерное уравнение

Экономичные схемы. Для уравнения переноса (лекция №10) хорошие схемы бегущего счета естественным образом обобщаются на многомерный случай. Для уравнения теплопроводности попытки обобщить хорошие неявные разностные схемы типа (6), (19),(20) на многомерный случай сталкиваются с принципиальными трудностями.

Рассмотрим эти затруднения на примере двумерного уравнения теплопроводности с постоянным коэффициентом теплопроводности, для которого определена первая краевая задача в прямоугольной по переменным x₁, x₂ области:

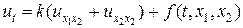, (34)

где k = const > 0, (t,x₁,x₂) Î G(t,x₁,x₂) = (0,T]´(0,a)´(0,b);

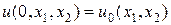; (35)

(36)


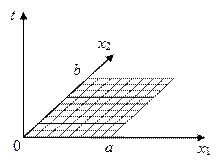
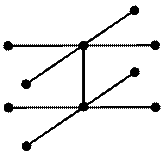
Рис.6,а. Определение прямоугольной равномерной сетки с шагами h₁, h₂ по переменным x₁, x₂	Рис.6,б. Шаблон разностной схемы (37)

Определим прямоугольную сетку (x_1,_n,x_2,_m) (рис.6,а), считая для простоты ее равномерной с шагами по переменным x₁, x₂ — h₁, h₂ соответственно, т.е. x_1,_n = h₁n, x_2,_m = h₂m, n = 0,1,…,N, m = 0,1,…,M. Выберем в качестве шаблона разностной схемы тот, который представлен на рис.6,б. На каждом временном слое шаблон имеет форму креста, по которому составляется неявная двухслойная схема с весом s, построенная по аналогии со схемой (6), т.е.

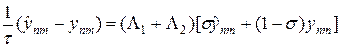, (37)

где

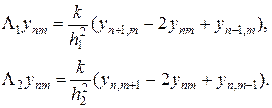(37¢)

Запись начального (35) и краевых условий (36) в разностном виде очевидна и реализуется точно. Можно проверить, что погрешность аппроксимации схемы (37), (37¢) на решениях с непрерывными четвертыми производными равна 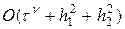, где n = 2 при s = ½ и n = 1 при s ¹ ½.

Исследуем устойчивость разностной схемы (37), (37¢) методом разделения переменных. Гармоники с текущего и следующего временного слоя выберем в виде:

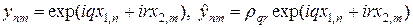тогда, считая как обычно модуль множителя роста 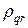меньше единицы, находим условие устойчивости разностной схемы (37), (37¢) в :

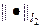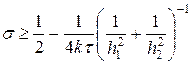, (38)

которое похоже на аналогичное условие (10) для одномерной схемы (6).

Схема (37), (37¢) легко обобщается на случай p измерений. Оценим число операций, требуемых для расчета до момента времени T.

Рассмотрим явную схему при s = 0, для которой значения 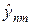вычисляются по значениям с предыдущего слоя, т.е. всего требуется ~ N^p операций, где для простоты считается, что число узлов по каждой переменной одинаково и равно N. Согласно (38), явная разностная схема устойчива, когда

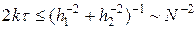Таким образом, для расчета до момента времени T необходимо сделать ~ N² шагов по времени и полный расчет потребует ~ N^p⁺² операций.

Если пользоваться абсолютно устойчивой схемой, когда s ³ ½, то можно выбирать t ~ h. Однако, в этом случае необходимо решать линейную систему уравнений порядка N^p. Если ее решать методом Гаусса, то потребуется ~ N³^p операций. Это число операций можно несколько сократить, заметив, что полученная матрица будет сильно разреженной и если предположить, что используется алгоритм, учитывающий такую разреженность, то число операций будет ~ N³^p^-². Такая оценка следует из того, что в одномерном случае матрица трехдиагональная и система уравнений решается прогонкой с числом операций ~ N. Учитывая, что для получения решения в момент времени T требуется ~ N шагов по времени, найдем итоговую оценку для числа операций ~ N³^p^-¹ при использовании неявной разностной схемы.

Если для одномерного уравнения явная схема является явно невыгодной на фоне использования неявных схем, то в многомерном случае (p ³ 2) неявные схемы становятся невыгодными по сравнению с явной схемой.

Несмотря на упомянутые выше трудности, для многомерного параболического уравнения построены абсолютно устойчивые разностные схемы, которые позволяют вести расчет с шагом t ~ h и требующие ~ N^p операций для перехода со слоя на слой. Это значит, что число действий в расчете на узел пространственной сетки не зависит от шагов h_a, a = 1,…,p. Такие схемы принято называть экономичными.

Подавляющее большинство многомерных расчетов параболических уравнений производится по экономичным схемам. Ниже будут рассмотрены два вида таких схем: продольно-поперечные и локально-одномерные.

Продольно-поперечная схема является одной из самых лучших двумерных экономичных разностных схем. Ее также называют схемой переменных направлений. На рис.7 приведен шаблон схемы переменных направлений, в которую введен полуцелый слой 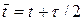. Составим согласно шаблону рис.7 разностную схему:

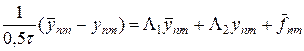, (39)

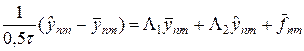, (39¢)

где разностные операторы L₁, L₂ определены в (37¢), а 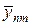берется на полуцелом слое .

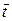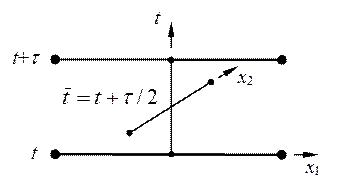
Рис.7. Шаблон разностной схемы (39), (39¢)

Исследуем продольно-поперечную разностную схему (39), (39¢).

Вычислительная процедура по схеме (39), (39¢) складывается из перехода со слоя t на слой 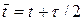согласно уравнению (39) и далее переход со слоя 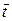на слой t + t согласно уравнению (39¢). На первом шаге неизвестными выступают величины 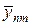с полуцелого слоя, они находятся прогонкой по направлению x₁ путем обращения разностного оператора L₁, который согласно (37¢) определен на трехточечном шаблоне. На втором шаге при переходе на слой t + t неизвестными выступают величины 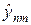, они находятся прогонкой, но в поперечном x₂ направлении путем обращения оператора L₂, который также определен на трехточечном шаблоне. И для первой, и для второй прогонки имеется диагональное преобладание так, что прогонки устойчивы, а разностное решение существует и единственно.

Устойчивость продольно-поперечной схемы можно исследовать методом разделения переменных. Положим

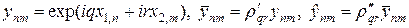, (40)

где 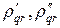— множители роста гармоник на первом и втором полушагах. Подставляя представление (40) в (39), (39¢), находим

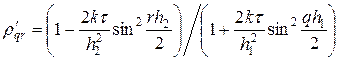, (41)

. (41¢)

Учитывая (40), (41¢), можно убедиться, что для любых гармоник и при любых шагах сетки верно неравенство: 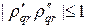. Таким образом, при переходе со слоя слой ошибки в начальных данных не растут и разностная схема (39), (39¢) равномерно и безусловно устойчива по начальным данным. Можно также проверить, что дополнительный признак устойчивости по правой части (9.65) выполняется на каждом из полушагов по времени, т.е. схема (39), (39¢) также устойчива по правой части.

Порядок аппроксимации схемы (39), (39¢) можно оценить путем исключения полуцелого слоя. Для этого вычтем из уравнения (39) уравнение (39¢), тогда найдем

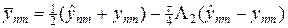. (42)

Складывая уравнения (39), (39¢) и подставляя в них выражение (42), получим

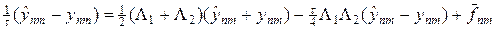. (43)

Предпоследний член в правой части (43), после разложения в ряд Тейлора, может быть аппроксимирован выражением . Остальные члены в (43) совпадают с симметричным вариантом схемы (37) (s = ½), которая имеет порядок аппроксимации 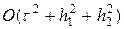. Тем самым, продольно-поперечная схема имеет второй порядок точности по всем переменным.

Определимся с аппроксимацией граничных условий (36) для продольно-поперечной схемы. При решении уравнения (39¢) относительно 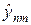необходимо использовать граничное условие на сторонах прямоугольника x₂ = 0 и x₂ = b. В этом случае очевидно можно положить, что

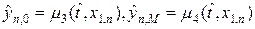. (44)

При решении уравнения (39) относительно 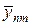необходимы граничные условия на сторонах x₁ = 0 и x₁ = a. Для их получения необходимо воспользоваться уравнением (42), тогда

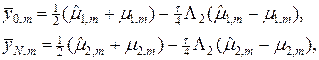(44¢)

где m = 1,…,M-1. Граничные условия (44), (44¢) обеспечивают погрешность аппроксимации .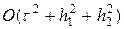

Проведенное исследование аппроксимации и устойчивости показывает, что схема (39), (39¢) безусловно сходится в норме 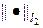, при этом в прямоугольной области на равномерной сетке и при граничных условиях (44), (44¢) схема имеет точность 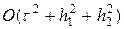на решениях с непрерывными пятыми производными.

Изучим разностную схему (39), (39¢) на примере численного решения уравнения (34) с правой частью вида:

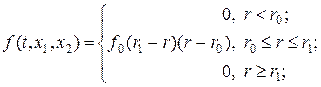(45)

где f₀, r₀, r₁ = const > 0, а 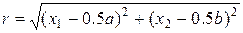. Функция (45) представляет собой источник тепла эллиптической формы в области [0,a]´[0,b]. Трехмерный график источника тепла представлен на рис.8 (левый рисунок). На листинге_№4 приведен код программы численного решения задачи (34), (45) с нулевыми граничными и начальными условиями.

Листинг_№4

%Программа решения двухмерного уравнения

%теплопроводности (34) с источником специального

%вида (45) с помощью продольно-поперечной

%разностной схемы (39), (39')

function heat_dim2

global a b f0 r0 r1

%Определяем габариты области интегрирования

%по времени, направлениям x1 и x2, а также

%коэффициент теплопроводности и константу f0,

%задающую амплитуду источника

T=1; a=1; b=1; koef=0.5; f0=100;

r0=0.2*min(a,b); r1=0.4*min(a,b);

%Определяем число шагов по времени и по

%направлениям x1 и x2

Nt=61; tau=T/(Nt-1);

N=61; M=61;

h1=a/(N-1); h2=b/(M-1);

%Определяем сетки по x1 и x2

x1=0:h1:a; x2=0:h2:b;

%Определяем источник тепла в узлах сетки

for n=1:N

for m=1:M

src(n,m)=f(x1(n),x2(m));

end

%Рисуем трехмерный профиль источника тепла

subplot(2,2,1); surf(x2,x1,src);

%Определяем нулевые начальные данные

for n=1:N

for m=1:M

y(1,n,m)=0;

end

%Определяем граничные условия при x1=0 и x1=a

for t=1:Nt

for m=1:M

y(t,1,m)=0; y(t,N,m)=0;

end

%Определяем граничные условия при x2=0 и x2=b

for t=1:Nt

for n=1:N

y(t,n,1)=0; y(t,n,M)=0;

end

%Определяем номера слоев по времени, которые будут

%нарисованы на итоговом графике

nt=[3 8 (Nt-1)]; k=1;

%Организуем основной цикл интегрирования по времени

for t=1:(Nt-1)

p1=(0.5*tau*koef)/h1^2;

p2=(0.5*tau*koef)/h2^2;

%Находим решение на полуцелом временном слое,

%т.е. решаем уравнение (39)

for m=2:(M-1)

%Учитываем нулевое граничное при x1=0

alpha(2)=0; beta(2)=y(t,1,m);

for n=2:(N-1)

alpha(n+1)=p1/(1+p1*(2-alpha(n)));

beta(n+1)=(y(t,n,m)+p2*(y(t,n,m-1)-...

2*y(t,n,m)+y(t,n,m+1))+...

0.5*tau*f(x1(n),x2(m))+...

p1*beta(n))/(1+p1*(2-alpha(n)));

end

%Учитываем нулевое граничное при x1=a

ys(N,m)=y(t,N,m);

for n=N:-1:2

ys(n-1,m)=alpha(n)*ys(n,m)+beta(n);

end

%Находим решение на следующем временном слое,

%т.е. решаем уравнение (39')

for n=2:(N-1)

%Учитываем нулевое граничное при x2=0

alpha(2)=0; beta(2)=y(t,n,1);

for m=2:(M-1)

alpha(m+1)=p2/(1+p2*(2-alpha(m)));

beta(m+1)=(ys(n,m)+p1*(ys(n-1,m)-...

2*ys(n,m)+ys(n+1,m))+...

0.5*tau*f(x1(n),x2(m))+...

p2*beta(m))/(1+p2*(2-alpha(m)));

end

for m=M:-1:2

y(t+1,n,m-1)=alpha(m)*y(t+1,n,m)+beta(m);

end

if nt(k)==t

k=k+1;

for n=1:N

for m=1:M

z(n,m)=y(t,n,m);

end

%Рисуем выбранные слои по времени

subplot(2,2,k); surf(x2,x1,z);

end

%Определяем функцию правой части уравнения (34)

function y=f(x1,x2)

global a b f0 r0 r1

r=sqrt((x1-0.5*a)^2+(x2-0.5*b)^2);

y=0;

if (r>=r0)&(r<=r1)

y=f0*(r1-r)*(r-r0);

end

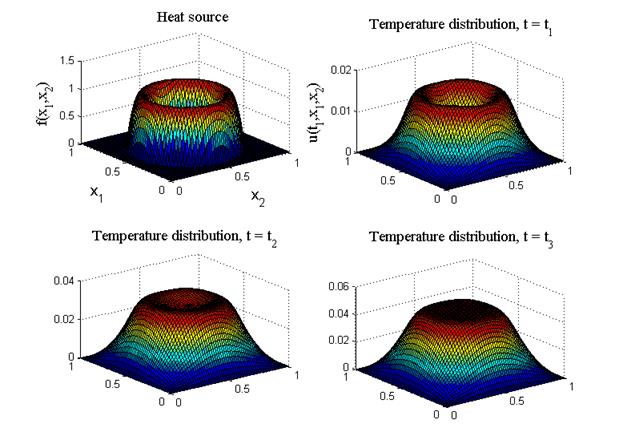
Рис.8. Численное решение уравнения теплопроводности (34) с
источником тепла (45)

Итог работы кода программы листинга_№4 приведен на рис.8. На левом верхнем рисунке приведен трехмерный профиль источника тепла (45), который имеет кольцевую форму. На трех других рисунках приведены трехмерные профили численных решений уравнения (34) с источником тепла (45) с помощью продольно-поперечной схемы (39), (39¢) в три различные момента времени t₁, t₂, t₃, причем t₁ < t₂ < t₃. Видно, как постепенно ямка в центре теплового возмущения исчезает и со временем становится еле заметной.

Локально-одномерный метод. Продольно-поперечная схема на задачи с числом измерений p ³ 3 не обобщается. Экономичные многомерные разностные схемы можно строить локально-одномерным методом, в которых также используются промежуточные слои, на которых численные решения вообще не аппроксимирует исходное дифференциальное уравнение. Однако при суммировании погрешности аппроксимации промежуточных слоев гасят друг друга и на целом слое аппроксимация имеет место, т.е. можно говорить о суммарной аппроксимации. Таким образом, физический смысл имеют лишь численные решения на целых, а не промежуточных, временных слоях.

Рассмотрим многомерное параболическое уравнение следующего вида:

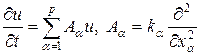, (46)

где k_a = const > 0, x = (x₁,…,x_p).

Аппроксимируем (46) симметричной неявной разностной схемой, т.е.

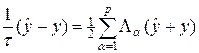, (47)

где L_a — разностные операторы типа (37¢), аппроксимирующие A_a с погрешностью O(h²), т.е. в целом схема (47) имеет погрешность 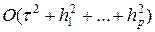. Схема (47) неэкономична, поскольку не найден экономичный алгоритм вычисления .

Исходя из (47), построим локально-одномерную схему. Обозначим решение на промежуточных шагах через w_a, a = 1,2,…,p и запишем для промежуточных слоев следующие разностные схемы:

; (48)

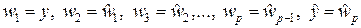. (49)

Поскольку каждая из схем (48) является одномерной, постольку и вся схема (48), (49) называется локально-одномерной. Проведем исследование схемы (48), (49).

Каждое из уравнений (48) является одномерной неявной симметричной схемой типа (6) при s = ½. Как установлена выше, эта схема является безусловной устойчивой, т.е. ошибка в начальных данных не возрастает ни на одном из промежуточных слоев. Тем самым, локально-одномерная схема (48), (49) является безусловно устойчивой.

Каждое уравнение в (48) решается прогонкой. По тем же соображениям, которые были высказаны относительно применения прогонки к схеме (6), прогонки для уравнений (48) устойчивы и разностное уравнение существует и единственно.

Для оценки порядка аппроксимации сравним схему (48), (49) со схемой (47). Представим уравнения (48) в виде

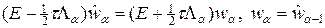. (50)

Поскольку операторы A_a, a = 1,…,p попарно перестановочны, постольку и их разностные аналоги L_a, a = 1,…,p также перестановочны. Последовательно применяя (50) ко всем промежуточным слоям, находим

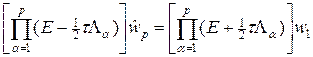. (51)

Раскрывая произведения в (51) и удерживая члены второго порядка малости по t, находим

. (52)

На решениях с непрерывными пятыми производными двойная сумма в (52) имеет порядок O(t²). Таким образом, локально-одномерная схема (48), (49) на целых слоях имеет порядок аппроксимации .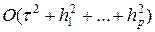

Для получения погрешности аппроксимации O(t²) для граничных условий необходимо удовлетворить уравнениям, аналогичным (44), (44¢).

Изучим локально-одномерный метод на примере решения уравнения (46) при p = 2, т.е. численно с помощью разностной схемы (48), (49) решим двумерное уравнение теплопроводности без источника. В этом случае разностные схемы (48), (49) можно переписать в виде:

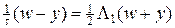, (53)

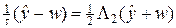. (53¢)

Для двумерного случая в локально-одномерной схеме — один-единственный промежуточный слой w. Значения на этом слое находятся решением уравнения (53) прогонкой и далее эти решения используются во втором уравнении (53¢), в котором опять же прогонкой получают искомые решения на следующем слое .

На листинге_№5 приведен код программы расчета по разностным схемам (53), (53¢) эволюции начального распределения температуры в виде конуса (левая фигура на рис.9).

Листинг_№5

%Программа расчета двумерного уравнения

%теплопроводности (46) по локально-

%одномерной разностной схеме (53), (53')

function heat_dim1p1

global a b r0 hg

%Определение габаритов области интегрирования

%по времени T, направлениям x1, x2, определение

%параметров начального распределения в виде

%конуса r0, hg и коэффициента теплопроводности koef

T=1; a=1; b=1; r0=0.25; hg=10; koef=1;

%Определение количества узлов сетки по времени Nt

Nt=151; tau=T/(Nt-1);

%Определение количества узлов сеток по

%направлениям x1,x2 - N, M соответственно

N=41; M=41;

h1=a/(N-1); h2=b/(M-1);

x1=0:h1:a; x2=0:h2:b;

%Определяем в виде двумерной матрицы начальное

%распределение температуры

for n=1:N

for m=1:M

ind(n,m)=u0(x1(n),x2(m));

end

%Рисуем начальное распределение температуры

subplot(1,2,1); surf(x2,x1,ind);

%Определяем начальное распределение температуры

for n=1:N

for m=1:M

y(1,n,m)=u0(x1(n),x2(m));

end

%Определяем нулевые граничные условия

%при x1=0 и x1=a

for t=1:Nt

for m=1:M

y(t,1,m)=0; y(t,N,m)=0;

end

%Определяем нулевые граничные условия

%при x2=0 и x2=b

for t=1:Nt

for n=1:N

y(t,n,1)=0; y(t,n,M)=0;

end

%Организуем основной цикл расчета по времени

for t=1:(Nt-1)

p1=(tau*koef)/(2*h1^2);

p2=(tau*koef)/(2*h2^2);

%Определяем нулевые граничные условия при

%x2=0 и x2=b для промежуточного слоя w

for n=1:N

w(n,1)=y(t,n,1); w(n,M)=y(t,n,M);

end

%Осуществляем прогонки по направлению x1

%при различных m

for m=2:(M-1)

alpha(2)=0; beta(2)=y(t,1,m);

for n=2:(N-1)

alpha(n+1)=p1/(1+p1*(2-alpha(n)));

beta(n+1)=(y(t,n,m)+p1*(y(t,n-1,m)-...

2*y(t,n,m)+y(t,n+1,m)+beta(n)))/...

(1+p1*(2-alpha(n)));

end

%Формируем решение на промежуточном слое w

w(N,m)=y(t,N,m);

for n=N:-1:2

w(n-1,m)=alpha(n)*w(n,m)+beta(n);

end

%Осуществляем прогонки по направлению x2

%при различных n

for n=2:(N-1)

alpha(2)=0; beta(2)=y(t+1,n,1);

for m=2:(M-1)

alpha(m+1)=p2/(1+p2*(2-alpha(m)));

beta(m+1)=(w(n,m)+p2*(w(n,m-1)-...

2*w(n,m)+w(n,m+1)+beta(m)))/...

(1+p2*(2-alpha(m)));

end

%Формируем решение на следующем слое

for m=M:-1:2

y(t+1,n,m-1)=alpha(m)*y(t+1,n,m)+beta(m);

end

for n=1:N

for m=1:M

z(n,m)=y(Nt,n,m);

end

%Рисуем распределение температуры u(T,x1,x2) в

%момент времени t=T

subplot(1,2,2); surf(x2,x1,z);

%Определяем функцию, задающую начальное

%распределение в виде конуса

function y=u0(x1,x2)

global a b r0 hg

y=0;

r=sqrt((x1-0.5*a)^2+(x2-0.5*b)^2);

if r<=r0

y=(hg/r0)*(r0-r);

end

На рис.9 приведен итог работы кода программы листинга_№5. На рисунке слева представлен внешний вид начального распределения температуры в виде конуса (при a = b). Поскольку уравнение (46) является уравнением теплопроводности без источника, а на границах области [0,a]´[0,b] поддерживается нулевая температура, постольку начальное возмущение должно со временем растекаться вследствие теплопроводности и амплитуда его должна стремиться к нулю при t ® ¥. На правом рисунке приведено численное решение уравнения (46) на конечный момент времени t = T из области решения G(t,x₁,x₂) = (0,T]´(0,a)´(0,b) по локально-одномерной разностной схеме (53), (53¢). Согласно этому рисунку начальное возмущение температуры в виде конуса благополучно растеклось, и максимум распределения стремится к нулю при t ® ¥.

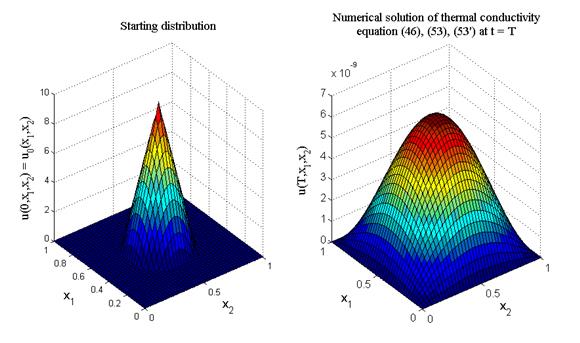
Рис.9. Начальное распределение температуры (рисунок слева) и численное
решение уравнения (46) по разностной схеме (53), (53¢) (рисунок справа)

[1] См., например, Тихонов А.Н., Самарский А.А. Уравнения математической физики. — М.: Наука, Гл. ред. физ.-мат. литературы, 1972.

[2] Режимы с обострением. Эволюция идеи: Законы коэволюции сложных структур/ Сб. статей/ Ред. Г.Г. Малинецкий/ Кибернетика: неограниченные возможности и возможные ограничения. — М.: Наука, 1999. 255с.

Дата добавления: 2016-03-27; просмотров: 2092;