Многомерное шкалирование

10.1 Метод многомерного шкалирования является своего рода альтернативой кластерному анализу. Исходным материалом для этих двух методов являются одна и та же матрица показателей сходства и различий: расстояний, коэффициентов корреляции или подобия. В кластерном анализе эти матрицы использовались для выделения групп наблюдений с относительно небольшими взаимными расстояниями. Цель многомерного шкалирования - в получении по этим матрицам такого наглядного графика, который в пространстве небольшого числа измерений (обычно 2 - 3) наглядно демонстрировал бы взаимное расположение изучаемых единиц в соответствии со значениями показателей их близости. Иными словами, целью многомерного шкалирования является построение такого графика, на котором визуально наблюдаемые расстояния между точками, представляющими единицы, были бы максимально сходными с реальными расстояниями, полученными по значениям признаков.

Таким образом, цели многомерного шкалирования можно формулировать так. Исходным материалом для него является матрица

0 D₁₂ D₁₃ ... D_1k

D₁₂ 0 D₂₃ ... D_2k

D = D₁₃ D₂₃ 0 ... D_3k , (9.1)

... ... ... ... ...

D_1k D_2k D_3k ... 0

включающая расстояния между k исследуемыми единицами. Необходимо построить график, опирающийся на небольшое количество (n) осей X₁, X₂, ..., X_n, на котором будут представлены точки, соответствующие этим единицам. Координаты точек для n осей X_i составляют прямоугольную матрицу

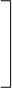
x₁₁ x₂₁ ... x_n1

x₁₂ x₂₂ ... x_n2

X = x₁₃ x₂₃ ... x_n3 . (9.2)

... ... ... ...

x_1k x_2k ... x_nk

Эта матрица называется конфигурацией многомерного шкалирования. По этим координатам можно вычислить расстояния между любой j-й и l-й точками на графике в виде метрики Евклида

_n

v_ij² = S (x_ij - x_il)² .

^{i = 1}

Расстояния v_ij можно увидеть непосредственно на графике, поэтому мы их будем в дальнейшем называть визуальными в отличие от эмпирических значений D_ij. Все эти вычисленные по графику визуальные расстояния между всеми точками составят матрицу

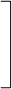
0 v₁₂ v₁₃ ... v_1k

v₁₂ 0 v₂₃ ... v_2k

V = v₁₃ v₂₃ 0 ... v_3k , (9.3)

... ... ... ... ...

v_1k v_2k v_3k ... 0

- 254 -

Очевидно, задача многомерного шкалирования сводится к нахождению на основе матрицы эмпирических расстояний D такой конфигурации X, чтобы найденная матрица визуальных расстояний Vнаилучшим образом соответствовала бы D. Это соответствие можно понимать двояко. Во-первых, можно требовать, чтобы между элементами матриц D и V существовала бы пропорциональность вида D_ij = c v_ij, где c - некоторая константа. Если соответствие двух матриц расстояния задано в столь жестком виде, многомерное шкалирование называется метрическим. Существует иной, более мягкий и гибкий принцип соответствия матриц D и V, по которому между D_ij и v_ij должны сохраняться соотношения упорядоченности, когда выполнение, например, неравенства D_ij < D_lt < D_pq влечет за сбой соблюдение аналогичной упорядоченности v_ij < v_lt < v_pq. Такое шкалирование называется неметрическим.

Многомерному шкалированию могут подвергаться также корреляционные матрицы, описывающие связи между признаками или между индивидами. В этом случае между коэффициентами корреляции r_ij и визуальными расстояниями между точками на графике должны соблюдаться обратные соотношения. При этом точки графика должны быть тем ближе, чем выше коэффициент корреляции между признаками или индивидами.