Графічне зображення хімічного потенціалу та зв’язок між інтегральними і парціальними властивостями.

На рис. 4.1 ми навели концентраційну залежність мольної енергії Гіббса, яка є інтегральною функцією. Ми вже знаємо, що парціальна мольна величина є частинною похідною екстенсивної функції по складу. Графічно це виглядає як дотична до концентраційної залежності самої функції в заданій точці складу. Такий графік показано нами рис. 4.2 для вільної енергії Гіббса двокомпонентного

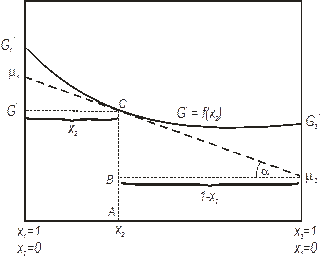
Рис. 4.2. Графічне зображення парціальних мольних величин для випадку хімічних потенціалів.

розплаву при заданих температурі і тиску. Вільна енергія Гіббса визначається як функція складу, парціальні мольні енергії Гіббса або хімічні потенціали компонентів 1 і 2 у розчині, m₁ і m₂, можуть бути отримані з мольної вільної енергії шляхом побудови дотичній до кривої у складі, що розглядається. На рис. 4.2 при складі х₂ мольна вільна енергія дорівнює G. Точки G₁ і G₂ відповідають вільним енергіям чистих розплавлених компонентів при заданих температурі і тиску. Дотична до кривої в точці, що відповідає складу x₂, перетинає ординати x₁ = 1 і x₂ = 1 при значеннях хімічних потенціалів компонентів 1 і 2, відповідно.

Покажемо, що відрізок АВ дорівнює хімічному потенціалу компонента 2, m₂. Дійсно, АВ = АС – ВС,

АС = G при х₂,

tga = -BC / 1-x₂ =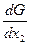

BC = -(1-x₂) tga = -(1-x₂)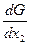

АВ = m_2.= G + (1-x₂) 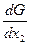(4.25)

Подібним чином можна показати, що

m₁ = G - x₂ 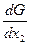. (4.26)

Отже, ордината дотичної при x₂ = 0 є m₁, при x₂ = 1 вона дорівнює m₂.

Це можна показати і аналітично.

Перепишемо рівняння (4.24) у вигляді

x₁(∂m₁/∂х₂) + x₂(∂m₂/∂х₂)= 0 (4.27)

Запишемо рівняння (4.25) у вигляді

G = m₁(1-x₂) + m₂x₂ (4.28)

і візьмемо диференціал по х₂:

(∂G/∂х₂) = m₂ - m₁ (4.29)

Рішаємо систему рівнянь (4.28) і (4.29):

m₂ = m₁ + (∂G/∂х₂)

G = m₁(1-x₂) + [m₁ + (∂G/∂х₂)]x₂ = m₁(1-x₂) + m₁x₂ + (∂G/∂х₂)x₂ = m₁ + (∂G/∂х₂)x₂

m₁ = G - x₂(∂G/∂х₂) (4.30)

m₂ = G - x₂(∂G/∂х₂) + (∂G/∂х₂) = G + (∂G/∂х₂)(1 - x₂), або

m₂ = G + х₁(∂G/∂х₂) (4.31)

Слід зазначити, що хімічний потенціал компонентів 1 і 2 у розчині змінюється зі складом розчину, так як різні дотичні перетинають ординати в різних положеннях. Парціальні молярні величини пов'язані між собою для розчину з фіксованим складом. До того ж, пов’язані між собою і парціальні і інтегральні мольні величини, як ми щойно бачили.

Отже, хімічний потенціал, виражений через енергію Гіббса, є парціальною мольною величиною. А чи є парціальними мольними величинами хімічні потенціали, виражені через вільну енергію Гельмгольца, ентальпію, внутрішню енергію? Відповідь – ні. В чому різниця між хімічним потенціалом і парціальними мольними величинами? Парціальні мольні величини визначаються при постійних температурі і тиску, хімічні потенціали – при постійних об’ємі і ентропії для внутрішньої енергії, постійних тиску і ентропії для ентальпії, постійних об’ємі і температурі для вільної енергії.

Найбільш широко застосовною парціальною мольною величиною, окрім хімічного потенціалу, є парціальна мольна ентальпія. Якщо хімічний потенціал більш застосовний для гетерогенних систем, то парціальна мольна ентальпія – для гомогенних.

Для парціальних мольних величин застосовні ті ж співвідношення, що і до термодинамічних функцій чистих речовин. Так, вільну енергію для вільної кількості розчину можна записати як

G = H – TS, (4.32)

а вільну енергію компоненту 1 у розчині, або парціальну вільну енергію компоненту 1 у розчині, або хімічний потенціал компоненту 1 як:

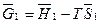= m₁ (4.33)

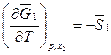, (4.34)

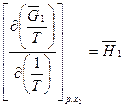. (4.35)