Відносні мольні величини.

Для встановлення термодинамічних функцій в розчині, як і для чистих речовин, дуже важливим є вибір стандартного стану для ентальпії і ентропії. При дослідженні розчинів часто буває достатньо визначити різницю функцій речовини в розчині і в чистому стані. Отже, за стандартний стан приймається функція чистої речовини, а вказана різниця називається відносною парціальною величиною, або функцією змішування. Наприклад, ентальпія змішування, енергія змішування, ентропія змішування. Її позначають верхнім індексом М або mix (від англійського mixing – змішування). Наприклад, U^M, U^mix, H^M, H^mix, S^M, S^mix, G^M, G^mix тощо. Тоді для речовини і можна записати:

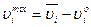(4.36)

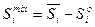(4.37)

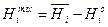(4.38)

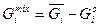, (4.39)

де υ_і^о, S_i^o, H_i^o, G_i^o – значення функцій у стандартному стані, яким є чисті речовини. Для останніх можна записати також υ_і^*, S_i^*, H_i^*, G_i^*. В даному випадку це тотожності. Графічно ці рівняння представлені на рис. 4.3 для ентальпії змішування.

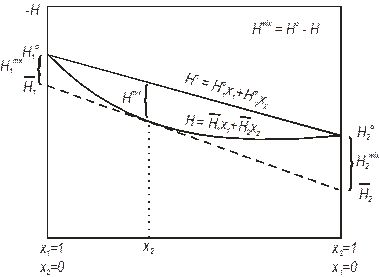
Рис. 4.3. Графічне визначення ентальпії змішування. H₁^mix і H₂^mix – парціальні ентальпії змішування компонентів 1 і 2, H^mix – інтегральна ентальпія змішування.

Різниця між парціальною і інтегральною величиною – в першому випадку незначна кількість речовини 2 додається до розчину, так, щоб його концентрація не змінилася. В другому випадку – до розчинника для утворення деякої заданої концентрації розчину. При малій концентрації розчину парціальні і інтегральні величини дуже близькі. При збільшенні концентрації різниця між ними збільшується.

До відносних мольних величин (величин змішування) також застосовні термодинамічні рівняння, наприклад:

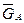( – G^*_А) = ( 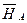– H^*_А) – T( 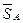– S^*_А). (4.40)

Отже, відносна парціальна мольна вільна енергія показує різницю між парціальною вільною енергією компонента А в розплаві і в чистому вигляді. Те ж саме – для інших екстенсивних величин.

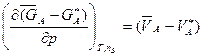, (4.41)

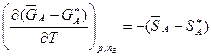, (4.42)

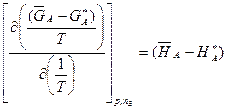. (4.43)

Ці рівняння показують зв’язок між інтегральними і парціальними мольними величинами.

Ідеальні розчини.

Ми вже знаємо, що неможна виміряти абсолютні властивості термодинамічних величин, а лише їх різницю з деяким стандартним станом. В теорії розчинів за стандартний стан взято ідеальний розчин. Найпростіший приклад ідеального розчину – це суміш газів. Газам притаманні слабка взаємодія між молекулами і великі відстані між ними. Тому гази змішуються в будь-яких пропорціях, звісно, при невеликих тисках. При атмосферному тиску –так. Газові суміші підпорядковуються закону Дальтона: загальний тиск суміші газів дорівнює сумі парціальних тисків усіх газів, що утворюють суміш:

Р_заг = ∑Р_і = (RT/V) ∑n_і (4.44)

P_i = (P₀n_i)/ ∑n_і = x_iP₀ (4.45)

P_i – парціальний тиск газу в суміші газів,

P₀ – тиск газу, якщо він сам займає весь об’єм,

x_i – мольна частка даного газу в суміші газів.

Парціальний тиск певного газу у газовій суміші, що займає об¢єм V, дорівнює тискові цього газу при умові, коли він сам займає весь об¢єм.

Щоб одержати зв¢язок між тиском газу і його хімічним потенціалом розглянемо систему, яка складається з посудини, що містить чистий газ з тиском Р. Якщо система знаходиться при постійній температурі і кількість газу залишається у ній незмінною, то з рівняння

dG = VdP – SdT + Sm_idn_i (4.46)

слідує, що dG = VdP. Для ідеальних газів, а гази при невисоких тисках і підвищених температурах є близькими до ідеальних,

PV = nRT (4.47)

Для 1 моля речовини n = 1

PV = RT (4.48)

V = RT/P (4.49)

Тобто

dG = (RT/P)dP = RT dlnP. (4.50)

Оскільки система є однокомпонентною,

dG = dm (4.51)

і

dm = RTdlnP (4.52)

Інтегруючи цей вираз, одержимо

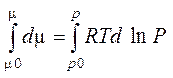(4.53)

або

m-m₀ = RT(lnP – lnP₀) = RTlnP/P₀ (4.54)

m = m₀ + RTlnP/P₀ (4.55)

m - хімічний потенціал газу при парціальному тискові Р,

m₀ - хімічний потенціал газу у стандартному стані, коли його тиск дорівнює Р₀ який, як правило обирають рівним атмосферному - 98.1 кПа (1 атм).

Звернімо увагу на те, що під логарифмом стоїть безрозмірна величина, тобто у яких одиницях ми б не вимірювали тиск, відношення Р/Р₀ буде однією і тією ж числовою величиною.

Закон Рауля.

Розглянемо тепер ідеальну рідину. Нехай вона однокомпонентна. На відміну від ідеального газу, в ідеальній рідині завжди існує взаємодія між молекулами. Як вже відзначалося, рівняння стану відоме лише для ідеальних газів (рівняння Менделєєва-Клапейрона). Тому в термодинаміці рідину описують через її насичену пару, які завжди знаходяться в рівновазі. Ця насичена пара також описується рівнянням (4.55)

m = m₀ + RTlnP/P₀.

Якщо в цій рідині розчинити інший компонент в незначній кількості, то його хімічний потенціал в розчині можна визначити з хімічного потенціалу парціального тиску його насиченої пари над розчином, адже парціальний тиск насиченої пари компоненту розчину прямо пропорційний його мольній частці в розчині. Коефіцієнт пропорційності дорівнює тиску насиченої пари над рідиною чистого компоненту.

Р_і = Р_і⁰х_і (4.56)

Р_і – парціальний тиск насиченої пари і-го компоненту над розчином;

Р_і⁰ – тиск насиченої пари над чистим компонентом;

х_і – мольна частка компоненту в розчині.

Звернемо увагу на те, що цей вираз аналогічний закону Дальтона (4.45).

Це є аналітичний вираз закону Рауля: Парціальний тиск насиченої пари компоненту розчину прямо пропорційний його мольній частці в розчині

Тоді

m_i = m_i⁰ + RTlnх_i(4.57)

Це рівняння справедливе для ідеальних розчинів. Якщо розчин реальний, то рівняння справедливе лище для розведених розчинів.

То що ж таке ідеальний розчин? Нехай розчин містить два компоненти, А та В. Існують сили тяжіння між однаковими атомами (А-А та В-В) і між різносортними атомами (А-В). Очевидно існують три можливості:

(1) сила тяжіння між різносортними атомами дорівнює силі тяжіння між однаковими атомами

А « B = 1/2(A « А + B « B)

(2) сила тяжіння між різносортними атомами більше сили тяжіння між однаковими атомами

А « B > 1/2(A « А + B « B)

(3) сила тяжіння між різносортними атомами менше сили тяжіння між однаковими атомами

А « B < 1/2(A « А + B « B).

Якщо реалізується перший випадок, розчин є ідеальним. Якщо реалізується другий випадок, сильніший зв'язок між різносортними атомами знижує ефективну концентрацію двох металів в розчині нижче їх фактичних концентрацій. Зворотне вірно для третього випадку.

Для опису реальних розчинів замість концентрації використовується поняття ефективної концентрації компонентів у розчинах, або термодинамічна активність. Що це таке? Ми вже домовилися, що тиск пари компоненту А в чистому вигляді дорівнює Р⁰_А. Якщо в компоненті А розчинити компонент В, тиск пари А зменшиться і дорівнюватиме Р_А. Відношення Р_А/Р⁰_А і є термодинамічною активністю:

а = Р_А/Р⁰_А (4.58)

Тоді

m_i = m_i⁰ + RTlna_i(4.59)

Для ідеальних і розведених реальних розчинів термодинамічна активність компоненту дорівнює його мольній частці.

а_і = х_і(4.60)

Розчин є ідеальним, якщо:

1. Він підпорядковується закону Рауля.

2. Зміна об’єму при змішуванні чистих компонентів дорівнює 0.

3. Теплота змішування дорівнює 0.

Реальні розчини

Ідеальних розчинів дуже мало, якщо взагалі є. Зазвичай, розчини показують відхилення від закону Рауля. Відхилення активності компонента в розчині виражається його коефіцієнтом активності, g, який дорівнює

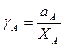(4.61)

Для ідеального розчину коефіцієнт активності дорівнює одиниці. Залежності активності від складу для ідеальних і реальних розчинів наведені на рис. 4.4. Реальні розчини (рис. 4.4 б та 4.4 в) підпорядковуються закону Рауля тільки при малому вміст розчиненої речовини. Негативне відхилення (рис. 4.4 б), з активностями меншими, ніж атомні частки, пов'язане з більшою силою тяжіння між атомами А і В, ніж між однаковими атомами. Таким чином, ефективна концентрація А зменшується, коли він утворює розчин із B. Така поведінка вказує на утворення проміжних фаз між А і В. Позитивне відхилення (рис. 4.4 в) вказує на тенденцію до розшарування фаз. На кінцях кривих спостерігається мала розчинність будь-якого з компонентів в іншому як у рідкому, так і у твердому стані.

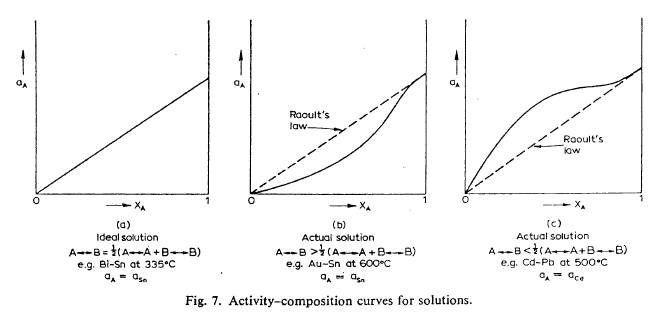
Рис. 4.4. Залежність активності розчинів від їх концентрації.

В реальних розчинах розчинник А підпорядковується закону Рауля тільки для розведених розчинів (з малим вмістом розчиненої речовини B). Розчинена речовина B у розведених розчинах підпорядковується закону Генрі:

а_В = kx_B. (4.62)

k – коефіцієнт Генрі.

Вираз (4.55) має важливе значення для практичної металургії, адже при вивченні систем дуже важливо знати тиск газів, що знаходяться у рівновазі з твердими фазами. Наприклад нас може цікавити питання, чи буде певна газова суміш, що містить кисень, при даній температурі окиснювати метал, чи окисел буде відновлюватися.

Розглянемо ще одне важливе питання, пов"язане з розчинністю двоатомних газів у металах. Умовно позначимо двоатомний газ через Н₂.

Реакція розчинення буде мати вигляд

1/2 Н₂ = [H] (4.62)

Якщо за стандартний стан ми обрали газ при тиску 1 атм, то з умов рівноваги

1/2 m_Н2 = m_[H] (4.63)

з урахуванням того, що

1/2 m_Н2 = 1/2m_Н2⁰ + 1/2 RT ln p_H2 (4.64)

m _[H] = 1/2m_Н2⁰ + RT ln a_[H] (4.65)

можемо записати

a_[H] = (p_H2)^1/2 (4.66)

Тобто, згідно з (4.61)

X_[H] = 1/g_[H] *( p_H2)^1/2 . (4.67)

Вираз (4.67) має назву закону Сівертсаіозначає, що при насиченні металів двоатомними газами концентрація газу у металі у межах розбавленого розчину (~ <3%) є прямо пропорційною кореню квадратному з парціального тиску газу.