Парціальні мольні величини.
Розглянуті раніше вирази для термодинамічних функцій застосовні для індивідуальних речовин незмінного складу, в яких не відбуваються фазові перетворення і стан яких цілком визначається параметрами р, v і Т при постійній масі. Такі речовини являють собою однокомпонентні гомогенні системи. До них можна віднести чисті метали при температурах нижчих або вищих за температуру плавлення. Якщо до речовини А додавати речовину В щоб вони утворювали механічні суміші різних пропорцій (суміш порошків металів), термодинамічні властивості суміші будуть змінюватися пропорційно вмісту речовини В, від властивостей чистого А до чистого В. Така зміна властивостей називається адитивною і графічно виражається прямою, як показано на рис. 4.1.
Рис. 4.1. Адитивна і неадитивна зміна вільної енергії Гіббса механічної суміші і фази змінного складу, відповідно.
Якщо ж ці порошки прореагували між собою і утворили твердий розчин, його властивості вже будуть залежати від складу нелінійно (рис. 4.1). Так поводяться фази змінного складу (рідкі розчини (розплави), тверді розчини, інтерметаліди з областями гомогенності) а також газові суміші.
Бачимо, що властивості речовин у розчині відрізняються від їх властивостей в механічних сумішах. При чому, в залежності від складу, ця різниця властивостей різна. Отже, термодинамічні рівняння мають враховувати склад таких речовин.
Для цього використовуються парціальні мольні величини, якими можуть бути всі екстенсивні термодинамічні функції. Що це таке? Уявімо собі, що у нас є розплав двох металів 1 і 2, який характеризується деякою екстенсивною величиною Y. Нею може бути вільна енергія G або F, об’єм v, вільна енергія U, ентальпія H, ентропія S. Додамо до нього при постійних температурі і тиску деяку кількість молів металу 2, dn2 так, щоб склад розчину не змінився. Як це може бути? Величина dn2 має бути дуже-дуже малою порівняно із загальною кількістю розплаву, або, навпаки, кількість розплаву має бути значно-значно більшою, ніж dn2. При цьому екстенсивна величина зміниться на величину, яка дорівнює
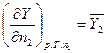(4.1)
При додаванні до розчину компоненту 1 у кількості dn1 так, щоб склад розчину не змінився, екстенсивна величина Y зміниться на
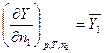(4.2)
Вирази (4.1) і (4.2) є парціальними мольними величинами компонентів 2 і 1, відповідно. Наприклад, для об’єму величини
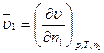та 
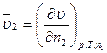(4.3)
називається парціальними молярними об'ємами компонентів 1 і 2. Парціальні молярні величини позначаються рискою зверху, а саме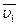 
, 
.
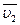Розглянемо далі об’єм υ як найбільш наочну властивість розчинів. Хоча всі подальші викладки справедливі для будь-якої екстенсивної величини Y.
Оскільки υ є функцією n1 тa n2, можна записати:
dυ =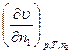 
dn1 +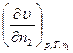 
dn2, (4.4)
або, враховуючи (4.3):
dυ =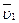 
dn1 +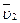 
dn2 (4.5)
Це рівняння справедливе для постійних 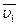та 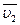, або при постійному складі розчину. Тоді після інтегрування маємо
υ = 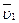n1 + 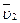n2 (4.6)
Якщо склад розчину змінюється, то величини 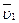і 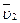будуть змінними. В цьому випадку продиференціюємо рівняння (4.6), одержимо
dυ = 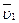dn1 + n1d 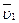+ 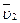dn2 + n2d 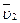(4.7)
Порівнюємо з (4.5), отримуємо
n1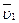d + n2d 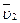= 0 (4.8)
Значно зручніше користуватися не кількістю молей, а мольними частками, які для металічних сплавів співпадають із атомними частками і дорівнюють
; 
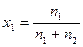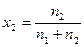= 1 – х1 (4.9)
Тоді всі величини будуть відноситися до 1 моля. Тоді рівняння (4.5), (4.6) і (4.8) зводяться до трьох основних рівнянь парціальних мольних величин:
dυ = 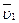dх1 + 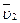dх2 (4.10)
υ = 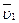х1 + 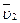х2 (4.11)
х1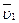d + х2d 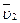= 0, (4.12)
або в загальному вигляді для будь-якої екстенсивної властивості:
dY =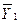 
dх1 +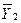 
dх2 (4.13)
Y = 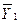х1 + 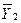х2 (4.14)
х1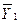d + х2d 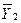= 0, (4.15)
Рівняння (4.15), або для об’єму (4.12), називається рівнянням Гіббса-Дюгема. Воно дозволяє розрахувати будь-яку парціальну мольну величину компоненту 1, якщо відома концентраційна залежність тієї ж парціальної мольної величини компоненту 2.
Парціальні мольні величини застосовують для опису термодинаміки гомогенних розчинів.
Дата добавления: 2016-02-27; просмотров: 1903;