Движение твёрдых тел и жидкостей в газе.
 Проведение рядов процессов химической технологии связано с движением твёрдых тел в капельных жидкостях и газах, к таким процессам относятся осаждение твёрдых частиц из суспензий и пыли, под действием силы тяжести, инерционных сил.
Проведение рядов процессов химической технологии связано с движением твёрдых тел в капельных жидкостях и газах, к таким процессам относятся осаждение твёрдых частиц из суспензий и пыли, под действием силы тяжести, инерционных сил.
Сила сопротивления среды.
При движении тел в жидкости или газах, возникают сопротивление их движению, для преодоления которого и последующего равномерного движения твердого тела должна быть затрачена энергия твердого тела. Величина возникающего сопротивления зависит, главным образом, от режима движения ( скорости) и форм обтекаемого тела.
Различают следующие движения твердого в жидкостях и газах.
 1) Ламинарный – имеет место при небольших скоростях движения и малых частиц.
1) Ламинарный – имеет место при небольших скоростях движения и малых частиц.
В ламинарном движении частицы обтекают равномерно, без завихрений, в данном случае потеря энергии связана с преодолением сил трения. При дальнейшем увеличении скорости движения возникает переходный , автомодельный режим.
В общем случае силу сопротивления среды можно рассчитать по закону сопротивления
R = ξ 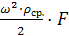
ξ- коэффициент сопротивления среды.
F- площадь проекции твердой частицы на плоскость перпендикулярную направлению движения.
rср – плотность среды.
w- скорость движения твердой частицы.
Для ламинарного режима движения при осаждении шарообразной частицы силу сопротивления можно найти по закону Стокса: R = 3·p· d· 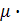 w
w
ξ= 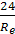 ; Для ламинарного режима
; Для ламинарного режима 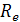 меньше 2.
меньше 2.
Для перехода области действия закон Алена согласно которому:
ξ= 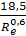 -Для переходной области 2<Rе< 500
-Для переходной области 2<Rе< 500
ξ= 0,44- Для автомодельной области Rе< 500
Для получения формулы для расчёта силы сопротивления среды может быть использована теория подобия при использовании метода анализа размерности.
R = f ( w, d, rср,m ср)
R = Аwа· dб· rвср·m ср г
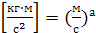 ·
· 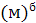 ·
· 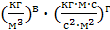
кг: 1 =в+г
м: 1 = а+в
с: -2 = -а-г
в = 1-г
а = 2-г
б = 1 – а + 3в + г = 1 – 2 + г + 3 – 3г + г = 2 – г
R = А·w2-г ·d2-г ·r1-гср·m ср г = А· ( 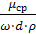 ) г ·d г ·w г ·rср
) г ·d г ·w г ·rср
R= y· 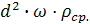
y=ξ 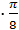
y- коэффициент сопротивления среды через опыт путь.
Для ламинарного движения: y= 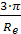
Для переходного режима: y= 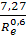 ;
;
Для автомодельного режима: y=0,174.
Рассмотрим силы действия на движущуюся частицу:
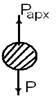 Результат сил действия на движущуюся частицу будет являться
Результат сил действия на движущуюся частицу будет являться  сопротивлением среды.
сопротивлением среды.
Ртяж = mт ·g = 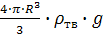
Рарх = mж ·g = 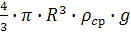
R= 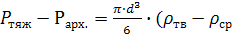 )
)
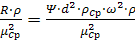 =
= 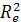
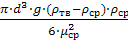 =Ψ·
=Ψ· 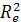
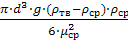 =Аr
=Аr
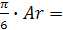 Ψ·
Ψ· 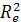
ля ламинарного режима движения:
Re= 0, 056 Аr Аr < 36
Переходный режим:
Re = 0,151 Аr0,71
Автомодельный режим:
Re=1,74·Ar0,5
| Режим | r | Re | y | Re=f(Ar) | Ar | wосаждения |
| Ламинарный | 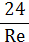
| Re < 2 | 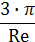
| Re= 0,056·Ar | Ar<36 | 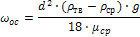
|
| Переходный | 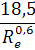
| 500<Re<2 | 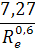
| Re=0,152· Ar 0,71 | 36<Ar<83·103 | 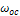 =0,78· =0,78· 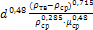
|
| Автомодельный | 0,44 | Re<500 | 0,174 | Re=1,74 · Ar0,5 | Ar<83 ·103 | 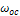 =5,45· =5,45· 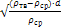
|
Скорость осаждения частицы.
Для определения скорости осаждения частицы необходимо силу сопротивления R приравнять к движущей силе процесса, при этом условии частичка будет осаждаться в среде с постоянной скоростью, которая называется скоростью осаждения. Для ламинарного режима, для шарообразной частички, сила сопротивления определяется по закону Стокса:
3· 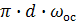 =g
=g 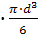 ·(
·( 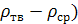
Условия свойства осаждения шарообразной частички для ламинарного движения определяется по закону Стокса:
Условия свойства осаждения шарообразной частички для ламинарного движения определяется по закону Стокса:
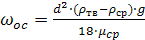 Ламинарный режим
Ламинарный режим
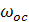 =0,78·
=0,78· 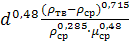 Переходный режим
Переходный режим
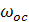 =5,45·
=5,45· 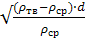 Автомодельный режим
Автомодельный режим
Методы расчёта скорости осаждения частиц.
1)Метод последовательных приближений.
Пользуясь формулой, начиная с ламинарного режима считаем скорость по формуле Стокса. Затем с учётом физических свойств среды рассчитывается критерий Рейнольдса пользуясь y (кол №3) получается ли данный режим, если нет то берем сл. режим и т.д.
2)Аналитический способ расчёта.
Заключается в следующем: рассчитывается критерий Архимеда Аг , по физическим свойствам среды и частички, тем самым определив режим движения, далее определяем критерии Рейнольдса по соответственной формуле, далее определяем wос.
3) Графический способ.
Разделение жидких и газовых неоднородных систем. Под неоднородными системами будем понимать системы, состоящие из двух фаз ( бинарные системы). Различают сплошную фазу (вода) и дисперсионную фазу ( взвешенные в ней твёрдые частички) в ходе процесса могут, манятся местами, такая перемена называется инверсия фаз.
Дата добавления: 2016-02-27; просмотров: 1477;
