Непрерывные распределения.

Равномерное распределение.

Равномерное распределение определяет случайную величину заданную на отрезке [a;b].

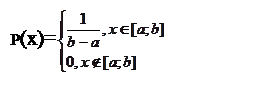
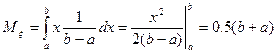
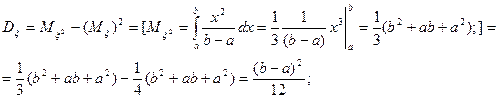
Показательное распределение .

Показательное распределение характеризует время безотказной работы в условиях эксперемента имеющего Распределение Пуассона.

ξ-время до первого отказа прибора:

F(x)=P(ξ<x)=1-p(0)=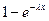

т.к. P(0)=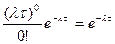

p(x)=F(x)=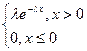

;

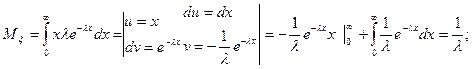
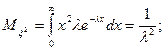
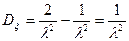Распределение нормальное.

Интеграл Лапласса 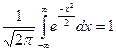, если выполним замену 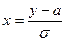, то получим наше распределение :

p(x)= ;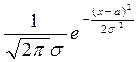

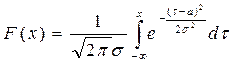
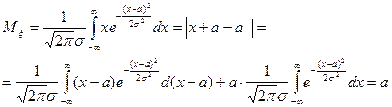
Т.к. 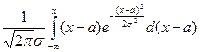=0 ,

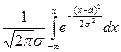а =1.

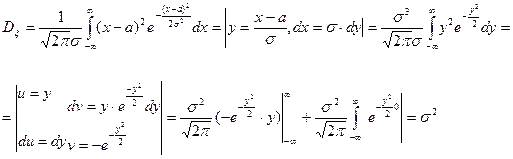
σ—среднеквадратическое отклонение нормального распределения.

Распределение Коши.

Пусть имеется источник излучения α-частиц.

ξ- случайная величина пересечения частицы с осью координат x.

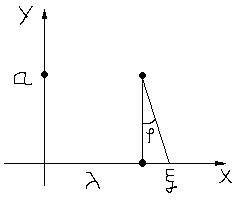
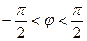
P(ξ<x)=P(tg (φ)< ).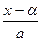

P(φ<arctg )=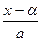

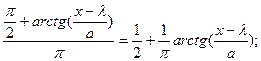
p(x)=P’(x)=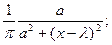

Распределение Коши не имеет мат.ожидания.

Распределение Вейбула –Гнеденко.

Это распределение используется в теории вероятностии и в теории надежности.

ק(x)=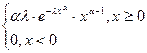

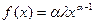-- функция интенсивности потока событий.

Если α=1 , то поучаем показательное распределение.

Распределение Лапласа.

p(x)=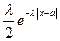

Данное распределение симметрично.