Формулы комбинаторики. Схема Бернулли.
Пример. Сколькими способами можно набрать семизначный номер телефона, если все его цифры различны. Очевидно, первую цифру можно набрать 10 способами, вторую - 9, так как одна цифра уже использована,...,седьмую - 4. Согласно правилу произведения общее число возможных номеров равно 10 × 9 ×8 × 7 ×6 ×5 ×4 = 604800.
Решение. Пусть из некоторого множества, состоящего из n различимых элементов, отбирается в определённом порядке m. Для подсчёта числа возможных вариантов заметим, что первый элемент можно выбрать n способами, второй – (n - 1), ..., m –й… (n - m + 1) способами. Согласно правилу произведения общее число вариантов будет равно n × (n - 1)-... (n - m + 1). Такие комбинации называют размещениями, а число вариантов обозначают 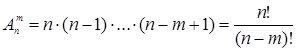 .
.
При n=m говорят о перестановках из n элементов, их число равно 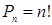 (n-факториал), т.е. 5!=1 ×2 ×3 ×4 ×5 или 7!= 1 ×2 ×3 ×4 ×5 ×6 ×7
(n-факториал), т.е. 5!=1 ×2 ×3 ×4 ×5 или 7!= 1 ×2 ×3 ×4 ×5 ×6 ×7
Пример. Формируется первая последовательность студентов в 6 человек для сдачи экзаменов в студенческой группе из 20 человек. Тогда число возможных вариантов
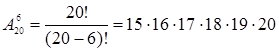
Если порядок отбираемых m элементов из n не играет роли, то говорят о числе сочетаний из n элементов по m. 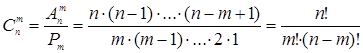
Пример. Сколькими способами можно из 20 присяжных заседателей отобрать трёх для участия в судебном процессе.
Решение. Поскольку несущественно, в каком порядке отобраны кандидатуры, число вариантов равно
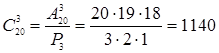
Рассмотрим стохастический эксперимент, который в свою очередь, является последовательностью n – независимых и однородных (одинаковых) испытаний, в результате каждого из которых может произойти событие а или ему противоположное 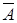 . С вероятностями р и q=1-р соответственно. По условию результат любого испытания не зависит от его порядкового номера и от того, что произошло до него. Простейшим примером может служить многократное бросание монеты. Когда с вероятностью р=0,5 выпадает герб и q= 0,5 – решка. Событие В, состоящее в том, что событие А наступило при каждом из m событий и не произошло при остальных n-m испытаниях можно записать в виде произведения
. С вероятностями р и q=1-р соответственно. По условию результат любого испытания не зависит от его порядкового номера и от того, что произошло до него. Простейшим примером может служить многократное бросание монеты. Когда с вероятностью р=0,5 выпадает герб и q= 0,5 – решка. Событие В, состоящее в том, что событие А наступило при каждом из m событий и не произошло при остальных n-m испытаниях можно записать в виде произведения 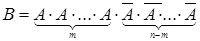
Так как все n испытания по условию независимы, то вероятность наступления события В равна произведению вероятностей наступления событий А и 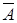 :
:
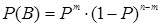 или
или 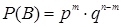
Число всевозможных различных последовательностей из n элементов, содержащих m элементов А, равно числу сочетаний 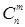 из элементов по m. Так как различные последовательности из m элементов А и n-m элементов
из элементов по m. Так как различные последовательности из m элементов А и n-m элементов 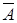 могут быть рассмотрены как различные исходы серии из n независимых испытаний, то все эти исходы (события) являются несовместными и искомая вероятность вычисляется по формуле Бернулли:
могут быть рассмотрены как различные исходы серии из n независимых испытаний, то все эти исходы (события) являются несовместными и искомая вероятность вычисляется по формуле Бернулли:
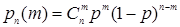 или
или 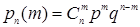
Дата добавления: 2016-02-27; просмотров: 1639;
