Понятие об итерационных методах решения СЛАУ.
В отличие от прямых методов, итерационные методы обычно не дают точного ответа за конечное число шагов, однако на каждом шаге уменьшают ошибку на какую-то долю. Итерации прекращают, когда ошибка становится меньше допуска, заданного вычислителем (пользователем). Величина финальной ошибки зависит от количества итераций, а также от свойств метода и СЛАУ. Другими словам, итерационные методы дают решение СЛАУ в виде предела последовательности некоторых векторов, построение которых осуществляется посредством единообразного процесса, называемого итерационным процессом.
Рассмотрим два простейших итерационных метода решения СЛАУ – метод простой итерации и метод Зейделя.
Пусть требуется решить СЛАУ
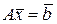 (2.3.1)
(2.3.1)
Итерационные методы решения системы уравнений (2.3.1) состоят в построении последовательности векторов
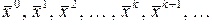 (2.3.2)
(2.3.2)
по некоторому алгоритму, такому, что из 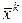 следует
следует 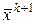 . При этом
. При этом
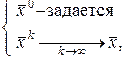 (2.3.3)
(2.3.3)
где 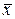 – точное решение системы, а
– точное решение системы, а 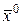 – называется начальным приближением решения.
– называется начальным приближением решения.
Вычисления ведутся до тех пор, пока норма разницы двух последовательных приближений не станет
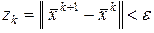 , (2.3.4)
, (2.3.4)
где e – малое положительное число (заданная точность). С точностью до e решение принимается равным 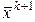 .
.
Дата добавления: 2016-02-27; просмотров: 487;
