Общие сведения о перекачке вязких и застывающих нефтей

Свойства жидкости, от которых зависит характер её течения, называются реологическими.

Движение реальной жидкости сопровождается потерей энергии, обусловленной вязкостью.

Поскольку существует несколько классов жидкостей, то опери­руют несколькими понятиями вязкости.

Для ньютоновской жидкости причиной потерь является не столь­ко трение о стенки трубопровода, сколько внутреннее трение жид­кости. Коэффициент динамической вязкости по кривой течения опре­деляется как

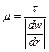
Вязкостно-температурную кривую нефти лучше получать в лаборатории; если нет такой возможности, то пользуются эмпирической формулой Рейнольдса-Филонова

, (7.1)

где U - коэффициент крутизны вискограммы, 1/K, ν_* - коэффициент кинематической вязкости при известной (произвольной) температуре Т_*. Для нахождения U достаточно знать ν₁ при Т=Т₁ и ν₂ при Т=Т₂.

Плотность нефти ρ при температуре Т может быть определена по формуле

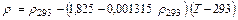, (7.2)

где ρ₂₉₃ - плотность нефти при температуре 293 К, кг/м³.

Расчетная плотность n нефтей с достаточной для практики точностью может быть определена

, (7.3)

где ρ_i - плотность i-й нефти объемом V_i в общем случае V.

Расчетную плотность нефти для трубопровода большой протя­женности, проложенного в n климатических зонах, усредняют с учетом климатических поясов:

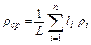, (7.4)

где 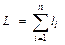- длина трубопровода; ρ_i - средняя плотность нефти на участке трубопровода длиной l_i с примерно одинаковой температу­рой.

Удельная теплоемкость С_р нефти изменяется в пределах 1600…2500 Дж/(кг∙К). При расчетах часто пользуются средним зна­чением С_р=2100 Дж/(кг∙К). Для диапазона температур 273…673 К С_р можно вычислять по формуле Крего;

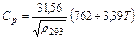. (7.5)

Коэффициент теплопроводности нефти λ_н изменяется в пределах 0,1…0,16. Обычно при расчетах используют среднее значение λ_н=0,13 Вт/(м∙К). Для более точных расчетов используют формулу Крего-Смита,

справедливую для температур 273…473 K.

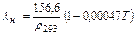. (7.6)

Для трубопроводов большой протяженности, прокладываемых в нескольких климатических зонах, расчетные теплоемкость и коэф­фициент теплопроводности усредняют по длине, аналогично усред­нению плотности, для этого в формулу (7.4) вместо ρ_i подстав­ляют C_pi или λ_нi.

Рассмотрим движение вязкой парафинистой нефти по трубопро­воду при неизотермическом установившемся режиме. Полагаем, что, если парафин кристаллизируется, то он уносится потоком, не осе­дая на стенках трубы.

В общем случае уравнение теплового баланса для элемента трубопровода длиной dx .отстоявшего на расстоянии x , будет

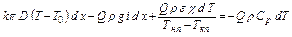(7.7)

Первое слагаемое-это потери в окружающую среду с эле­мента трубопровода длиной dx (k - коэффициент теплопередачи; D - внутренний диаметр трубопровода; Т - температура неф­ти в трубопроводе на расстоянии X от начала; Т₀ - темпе­ратура окружающей среды (грунта), постоянная, осредненная по длине).

Второе слагаемое представляет собой теплоту трения в рассматриваемом сечения (Q - объемный расход нефти ρ - плотность нефти, i - гидравлический уклон). Так как теплота трения час­тично компенсирует теплопотери, то перед вторым слагаемым постав­лен знак минус.

Третье слагаемое - это тепло, выделяющееся при кристаллизации парафина (ε - массовое содержание парафина в нефти (в долях); χ - теплота кристаллизации; Т_нп и Т_кп - соответственно тем­пература начала и конца выпадения парафина). Тепло кристаллизации также частично компенсирует теплопотери в окружающую среду. Но, имея в виду, что dT отрицательное (температура по длине па­дает), то знак перед третьим слагаемым будет плюс (минус на ми­нус дает плюс).

В правой части уравнения теплового баланса записано измене­ние теплосодержания (С_р - теплоемкость нефти). Так как гра­диент отрицательный, то принят знак минус.

Приняв среднее значение гидравлического уклона, разделяя переменные, интегрируя и имея в виду, что при X = 0, Т=Т_н, получим

, (7.8)

или

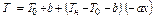, (7.9)

где ; ; .

Если парафин отсутствует, то положив ε=0, из (7.8) и (7.9) получим формулу Лейбензона. Если к тому же нефть маловязкая, то можно пренебречь теплотой трения (b= 0) и из (7.8) и (7.9) получим формулу Шухова. Для маловяз­кой, но парафинистой нефти в формуле (7.9) следует положить b=0.

Характер изменения температуры по длине трубопровода для различных нефтей показан на рис. 7.1. Видим, что самые высокие темпы снижения температуры присущи формуле Шухова. Тепло тре­ния и теплота кристаллизации снижают интенсивность охлаждения жидкости в трубопроводе.

Рис. 7.1. Изменение температуры нефти по длине трубопровода:

1 – по формуле Шухова, С^*_p=С_р , b=0; 2 – по формуле Лейбензона, ε=0;

3 – по формуле (7.9), С^*_p>С_р ,ε≠0 , b≠0; 4 – по формуле (7.9), С^*_p>С_р ,ε≠0 , b=0

Расчет теплового режима магистрального трубопровода являет­ся трудоемким, так как в общем случае могут быть участки, где парафин не выпадает (Т_н>Т_нп и Т>Т_кп) и где он выпадает (Т_нп≥Т≥Т_кп). В области высоких температур можно не учиты­вать теплоту трения, а при низких температурах она составляет значимую долю в тепловом балансе. Кроме этого, в трубопроводе могут быть два режима течения: на начальном участке, где темпе­ратуры высокие, возможен турбулентный режим течения, а на остав­шейся длине - ламинарный. Трудность расчета заключается в согла­совании условий на границах различных участков. Для упрощения изложения будем рассматривать случай наиболее интенсивного охлаждения, т.е. температура по длине трубопровода выражается формулой Шухова, которая получается из (7.8) при b=0, ε=0;

, (7.10)

Применяя ее к турбулентному участку, надо положить К=К_т: (см. рис. 7.2). В конце турбулентного участка температура

, (7.11)

где ; 0 ≤ X ≤ L; T_н ≥ T ≥ T_кр (см. рис. 7.2).

Рис. 7.2. Течение нефти в трубопроводе при двух режимах

В конце трубопроводного участка температура

, (7.12)

или

.

По аналогии для ламинарного участка можно записать (при К = К_л)

, (7.13)

где ; L_Т ≤ x ≤ L; T_кр ≥ T ≥ T_к

В конце ламинарного участка температура

, (7.14)

или

.

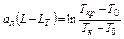На основании (7.12) и (7.14), исключая L_Т, можно получить соотношение, связывающее все граничные температуры в трубопро­воде с двумя режимами течения:

Критическую температуру Т_кр, соответствующую переходу турбулентного режима в ламинарный (и наоборот), определяют сле­дующим образом. Исходя из критического значения параметра Re≈2000, находим соответствующий ему коэффициент кинема­тической вязкости

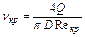. (7.15)

Затем по вискограмме для данной нефти находим Т_кр. Ее можно найти и аналитически. Например, подставив в формулу (7.1) ν_кр и Т_кр и решая совместно с (7.15), найдем

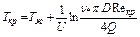. (7.16)

Используя другие аналитические зависимости для вязкости, можно найти соответствующие им формулы для Т_кр.

Коэффициент теплопередачи для трубопроводов зависит от внутреннего α₁ и внешнего α₂ коэффициентов тсплоотдачи, а также от термического сопротивления стенки трубы, изоля­ции, отложений и т.п.

, (7.17)

где D - внутренний диаметр трубопровода; n - число слоев, учитываемых в термическом сопротивле­нии при расчете; λ_i коэффициенты теплопроводности слоев (отложений, стали трубы, изоляции и т.п.); D_i, D_нi - соответственно внутренний и наружный диаметры каж­дого слоя; D_н - наружный диаметр трубопровода (диаметр поверхности, соприкасающейся с грунтом).

Для определения α₁ при вынужденном движении жидкости имеются различные экспериментальные зависимости, например, по Михееву (см. формулы 7.26, 7.27).

Теплофизические характеристики в приведенных зависимостях определяются при средних температурах потока и стенки трубы (индекс «СТ»), а за определяющий размер принят внутренний диаметр трубы. Теплофизические характеристики рассчитываются по формулам Крего.

В переходной области внутренний коэффициент теплоотдачи α₁, можно определять приближенно интерполяцией.

Для внешнего коэффициента теплоотдачи α₂ подземного трубопровода используют формулу Форхгеймера-Власова

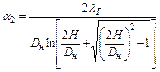, (7.18)

где λ_Г - коэффициент теплопроводности грунта; Н - глубина заложения трубопровода в грунт (до оси). При 2Н/Д_н > 2 (с погрешностью до 1 %)

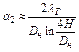. (7.19)

При малых заглублениях (H/D_н<3-4) пользуются формулой Аронса-Кутателадзе

, (7.20)

где 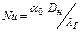; Н_п - приведенная глубина укладки трубопровода, которая складывается из геометрической глубины заложения Н и эквивалентной глубины Н_э, определяемой по выражению

. (7.21)

H_СН - толщина снежного покрова; λ_СН - коэффициент теплопроводности снега (λ_СН ≈ 0,105 Вт/(м∙K) - для свежее выпавшего снега; λ_СН≈0,465 Вт/(м∙K) - для уплотненного снега); α₀ - коэффициент теплоотдачи от поверхности грунта в воздух, при расчетах принимают α₀ ≈ 11,63 Вт/(м∙K).

Для подземных и особенно теплоизолированных трубопроводов при турбулентном режиме течения α₁ >> α₂, поэтому в большинст­ве случаев значением 1/α₁ D в формуле (7.17) можно пренебречь. Для трубопроводов без специальной тепловой изоляции, прокладываемых в грунтах малой влажности, при турбулентном режиме течения с малой погрешностью можно принять К ≈ α₂. При оценочных расче­тах коэффициент теплопередачи К принимают:

· для сухого песка 1,163 Вт/(м∙К),

· для влажной глины 1,454 Вт/(м∙К),

· для морского песка 3,489 Вт/(м∙К).

Расчет падения температуры можно выполнить более точно, если перегон разбить на отдельные участки в зависимости от грунтовых условий. Этот же расчет можно проводить по некоторому среднему значению λ_Тср. Падение температуры рассчитывают либо, начиная с головного участка при известной начальной температуре подогрева, либо с конца участка при известной конечной температуре.

7.2. Тепловой режим «горячего нефтепровода»

Цель задачи:

1) выяснить закон падения температуры по длине неизотермического нефтепровода;

2) определить полный коэффициент теплопередачи К от нефти через стенку в окружающую среду методом последовательных приближений.

Для расчета задаются следующие данные: D-диаметр нефтепровода внутренний, [м]; δ-толщина стенки нефтепровода, [м]; Q-производительность нефтепровода, [м³/c]; L-длина нефтепровода, [м], Т - начальная температура или температура подогрева нефти, [К]; Т – температура окружающей среды, [K]; λ_гр – коэффициент теплопроводности грунта, [Вт/м∙К]; Н-глубина заложения трубопровода до оси трубы, [м]; ρ₂₀- плотность нефти при 20 ⁰С, [кг/м³]; ν₂₀ – вязкость нефти при 20 ⁰С, [м²/с]; ν₅₀ – вязкость нефти при 50 ⁰С, [м²/с]; С – теплоемкость нефти для предварительных расчетов, [Дж/кг∙К].