Применение алгоритмов трассировки монтажных соединений при построении модели РЭС
Трассировка является заключительным этапом конструкторского проектирования. Для решения задач трассировки необходима исходная информация (список цепей, конструкция печатных плат, размеры контактных площадок, данные о размещении элементов).
На этапе трассировки необходимо в соответствии с электрической принципиальной схемой выбрать порядок соединения выводов (контактов) и определить конкретную геометрию трассы.
В отличие от алгоритмов компоновки и размещения, алгоритмы трассировки являются специализированными, поскольку трассировка зависит от многих технологических и конструктивных ограничений, к которым относятся: количество слоев для трассировки, допустимы пересечения или нет, допустим ли переход со слоя на слой, ортогональная трассировка или нет и т.п.
Специфика выполнения соединений проводным или печатным монтажом также требует различных методов трассировки.
Проводной монтаж, несмотря на широкое применение печатного, занимает значительное место при проектировании специализированной (военной техники). Для проводного монтажа применяются алгоритмы построения минимальных деревьев – соединений с минимальной длиной соединительных жгутов. Полная монтажная схема (таблица соединений) получается при последовательном применении алгоритмов для отдельных цепей схемы. В проводном монтаже применяют два алгоритма:
- алгоритм Прима;
- алгоритм Краскала.
Суть алгоритма Прима заключается в последовательном наращивании дерева соединений.
Печатный монтаж.Проектирование печатного монтажа является одной из самых сложных задач автоматизации проектирования.
Особенности печатного монтажа (ПМ) заключаются в следующем:
- недопустимость пересечения трасс, расположенных в одной монтажной плоскости;
- возможность, кроме соединений типа «вывод – вывод», использовать соединения типа «вывод – проводник» и «проводник – проводник».
Использование соединений такого типа предполагает решение задачи Штейнера: для заданного множества вершин, фиксированных на плоскости, требуется найти такую систему прямолинейных отрезков, чтобы любые две из данных точек могли быть соединены системой отрезков, причем общая длина системы была бы минимальной, т.е. при такой постановке задачи построение кратчайшей связывающей сети возможно при введении дополнительных узлов (вершин).




 2
2
 1 3
1 3

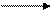
 4
4
2 4
1 
 3
3
Рисунок 3.7 – Иллюстрация решения задачи Штейнера.
В общем случае задача трассировки сводится к построению минимальных связывающих деревьев для различных электрических цепей и нахождению кратчайших соединений между парами вершин. Трассировка соединений осуществляется по следующим критериям:
- Минимум суммарной длины всех проводников;
- Минимум длины отдельных наиболее длинных связей;
- Равномерное распределение проводников на плате;
- Минимум числа пересечений всех проводников;
- Минимум изгибов или изломов проводников.
Критерии 1, 2, 3 влияют на скорость сигнала (препятствуют возникновению задержек) и помехоустойчивость. Критерии 4, 5 уменьшают число перемычек или переходов со слоя на слой, что улучшает технологичность печатной платы и повышает ее надежность. Критерий 4 улучшает возможности проведения всех трасс и уменьшает паразитные связи между проводниками. Критерий 5 применяется для повышения надежности и технологичности.
Данные критерии противоречивы по своей сути. Обычно учитывается один основной или устанавливается приоритет критериев, поскольку все критерии выполнить на практике невозможно.
Задача трассировки имеет топологический и метрический аспекты. Она включает следующие этапы:
1.Получение списка цепей.
2.Построение графа.
3.Анализ планарности графа.
4.Выделение плоских подграфов.
5.Разделение на слои.
Дата добавления: 2016-02-24; просмотров: 990;
