Изумительная биологическая машина

Звук на анализе

Вы тронули гитарную струну. Она пришла в движение, увлекла за собой окружающий воздух, и во все стороны от колеблющейся струны пошли звуковые волны. В самых общих чертах процесс образования и распространения звуковых волн выглядит так.

Двигаясь, струна сжимает воздух впереди себя, создает повышенное давление. Разумеется, область с повышенным давлением не может оставаться изолированной. Давление передается соседним участкам, и от струны катится своеобразный вал сжатого воздуха.

Но струна не просто движется – она совершает колебания. Это значит, что через некоторое время струна пойдет в обратную сторону, и там, где только что происходило сжатие воздуха, начнется его разрежение. Пониженное давление также передается соседним участкам, и вслед за валом сжатия следует вал разрежения. Затем струна вновь меняет направление, и за разреженной областью появляется область сжатия, за ней опять разрежение и т. д., до тех пор пока струна колеблется. Бегущие одна за другой области сжатия и разрежения – это как раз и есть звуковые волны.

Звуковые волны чем‑то напоминают волны на поверхности воды. Гребень морской волны можно сравнить с областью сжатого воздуха, впадину – с областью разрежения. В обоих случаях само вещество – воздух либо вода – не переносится вместе с волной, а лишь совершает колебание: поднимается – опускается, либо сжимается – разрежается.

У морских волн колебания происходят перпендикулярно направлению движения самой волны – волна движется горизонтально, а вода колеблется вверх‑вниз. Такие волны называют поперечными. У звуковой волны колебания направлены вдоль линии распространения, проще говоря – вперед‑назад. Поэтому звуковые волны называют продольными. Кстати, продольные волны могут распространяться в воде так же, как и в любой другой жидкости или твердом теле. При этом происходит ничтожное, измеряемое микронами и миллионными долями микрона, смещение вещества вперед‑назад.

Вернемся к «учебной» струне, график колебаний которой приведен на рис. 1. Поместим на некотором расстоянии от струны манометр, который будет измерять давление воздуха, и будем записывать все результаты измерений (рис. 4).

Рис. 4. График изменения звукового давления как бы повторяет график колебаний струны. Запаздывание звука зависит от расстояния до звучащего тела (струна) и может быть подсчитано, исходя из того, что скорость звука в воздухе при 0° примерно равна 330 м/сек.

Мы вводим такой прибор, конечно, условно: для нас это как бы мысленный эксперимент. Но такие измерения все же можно сделать с помощью электронных приборов.

Отрегулируем манометр так, чтобы он показывал лишь отклонение давления воздуха от обычной величины. Это значит, что при нормальном атмосферном давлении прибор покажет нуль. Под действием звуковых волн стрелка манометра будет отклоняться то в одну, то в другую сторону, показывая то сжатие (+), то разрежение (–). График изменения звукового давления (часто его называют графиком звуковых колебаний) в точности повторяет график изменения скорости струны. Здесь, правда, нужно сделать оговорку. Все графики, приведенные на рис. 1 (отклонения, скорости, энергии), очень похожи, и поэтому график звука можно зачислить в «родственники» к любому из них. И все же мы будем считать, что звуковое давление следует за изменением скорости: чем быстрее движется струна, тем большее давление она создает.

Сравнивая графики колебаний струны и звуковых колебаний, сразу же введем уже знакомые нам основные характеристики, или, как принято говорить, параметры звука: период, частоту, фазу, мгновенное значение и амплитуду. Разумеется, все эти параметры теперь относятся к звуковым колебаниям, то есть к изменению давления воздуха. Что касается периода, частоты и фазы, то с этими параметрами дело обстоит довольно просто – они, как и прежде, измеряются в секундах, герцах, градусах. А вот амплитуда и мгновенные значения должны быть выражены в единицах давления.

Как известно, давление говорит о той силе, которая действует на определенную поверхность. Поэтому единица давления представляет собой единицу силы, или, что то же самое, единицу веса, отнесенную к единице площади. В новой международной системе единиц СИ давление измеряют в ньютонах на квадратный метр, или, сокращенно, н/м². Ньютон (н) в системе СИ – это величина силы (веса), которая примерно равна 92 г. Таким образом, если на стандартный лист фанеры площадью около 2 м² мы выльем стакан воды (вес около 200 г) и равномерно распределим эту воду по листу, то каждый его участок будет испытывать давление около 1 н/м².

Единицей звукового давления н/м² стали широко пользоваться сравнительно недавно, и в литературе прежних лет вы встретите другую единицу – бар (дин/см²), который в 10 раз меньше 1 н/м², то есть 1 н/м² = 10 бар; 1 бар = 0,1 н/м².

Если вы захотите сказать, насколько сильный звук действует в какой‑либо точке пространства, то наверняка назовете величину звукового давления в этой точке. Но какую величину надо назвать? Мгновенное значение ни о чем не скажет, так как оно непрерывно меняется. Называть амплитуду тоже не совсем правильно – ведь амплитудное давление бывает сравнительно редко, всего два раза за период, а все остальное время звуковое давление значительно меньше.

Когда говорят о звуковом давлении, то обычно имеют в виду его так называемую эффективную величину. Она учитывает тот эффект, который производит звуковая волна в среднем за весь период, и поэтому эффективная величина всегда меньше амплитуды. Так, в частности, для звуковых колебаний, график которых показан на рис. 4, эффективное звуковое давление меньше амплитудного на 30 %. В дальнейшем, когда мы будем говорить о звуковом давлении, то всегда будем иметь в виду эффективное, или действующее, значение.

Если поместить на пути звуковой волны легкую пластинку, например листок бумаги, то волна заставит эту пластинку двигаться, совершать колебания. Как мы увидим дальше, такие вынужденные колебания тонких пластинок‑мембран лежат в основе работы многих музыкальных инструментов, микрофонов, человеческого уха.

О способности звуковой волны выполнять работу, например раскачивать листок бумаги, можно судить по звуковому давлению. Однако чаще работоспособность волны характеризуют так называемой интенсивностью или силой звука. Величина эта показывает, какая звуковая мощность приходится на единицу поверхности, на которую падает волна звука.

В системе СИ единицей силы звука служит ватт на квадратный метр – вт/м². Раньше пользовались другой единицей: мощность относили к площади в квадратный сантиметр – 1 вт/см² = 10000 вт/м²; 1 вт/м² = 0,0001 вт/см².

Если бы марсианину, прилетевшему на Землю, сказали, что у нас единицей длины служит метр, а единицей времени – секунда, то он наверняка попросил бы, чтобы ему пояснили, много это или мало. Так и вы, по‑видимому, тоже хотите знать, как выглядят и «чего стоят» применительно к звуковым волнам единицы н/м² и вт/м². В дальнейшем мы часто будем встречаться с этими единицами, а пока для их характеристики приведем лишь три примера.

Шорох листьев на расстоянии 1 м создает звуковое давление около 0,0001 н/м² (это в 10 тысяч раз меньше, чем давление стакана воды, распределенной по листу фанеры) и силу звука около 0,00000000001 (10^‑11) вт/м². На шумной улице звук, конечно, намного громче. Звуковое давление здесь достигает 0,2 н/м², а сила звука 0,0001 вт/м². Наконец, мощный реактивный двигатель на расстоянии 5 м создает звуковое давление 20 н/м² и силу звука около 1 вт/м².

Следующие два параметра звука, с которыми нам предстоит познакомиться, – это скорость распространения и длина волны.

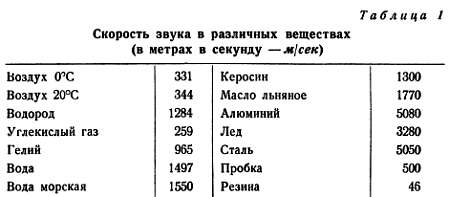
Если вы взглянете на график звука и график колебаний струны (рис. 4), то сразу же заметите их различие – звуковые колебания несколько запаздывают. В нашем примере они в точности следуют за всеми колебаниями струны, но следуют с опозданием на 0,1 сек. Это время необходимо звуковой волне для того, чтобы добежать от струны до той точки, где мы измеряем давление. Если измерить расстояние между струной и нашим воображаемым манометром, то можно подсчитать скорость распространения звуковой волны. Скорость звука, измеренная таким способом в различных веществах, приведена в табл. 1. Можно решить и обратную задачу. Взяв из этой таблицы скорость звука в воздухе (330 м/сек) и вспомнив, что опоздание звука составляет 0,1 сек, мы легко определим расстояние между струной и манометром. Оно составляет 33 м. Подобным же образом, заметив, на сколько секунд запаздывает гром, легко подсчитать расстояние до места вспышки молнии.

Что такое длина звуковой волны, легко понять, если вспомнить наше старое сравнение – с морскими волнами. Там длиной волны называют расстояние между двумя ближайшими гребнями или двумя ближайшими впадинами. Аналогично для звука длина волны – это расстояние между двумя ближайшими участками с максимальным (амплитудным) давлением или максимальным разрежением воздуха.

Длина звуковой волны зависит от частоты и скорости распространения звука. Чем выше частота, тем чаще следуют друг за другом области сжатия и разрежения, тем, следовательно, короче волна. А с увеличением скорости звука длина волны, наоборот, увеличивается. Чем быстрее распространяется звук, тем дальше успевает уйти один гребень от другого, тем больше расстояние между ними.

Нужно сказать, что акустика имеет дело со сравнительно короткими волнами. Так, например, при частоте 100 гц длина звуковой волны 3,3 м; частоте 500 гц соответствует волна 66 см, а частоте 20 кгц – 1,7 см. Данные эти относятся только к воздуху, к скорости звука 330 м/сек. В другой среде, с иной скоростью распространения звука, и длина волны будет иной. Так, в воде звук распространяется намного быстрее, и за время одного периода гребень звукового давления успевает пройти в четыре раза большее расстояние, чем в воздухе. Поэтому расстояние между гребнями, то есть длина волны в воде, также в четыре раза больше. Для приведенных выше значений частоты мы получим примерно такие длины волн: 14 м, 280 см и около 7 см.

Для распространения звука в плотной среде, в частности в жидкости, важна еще одна особенность. Звуковые волны, особенно самые длинные, не встречают значительного сопротивления, хорошо сохраняют энергию, полученную от излучателя, и поэтому проходят весьма большие расстояния. Это позволяет пользоваться звуком для дальней подводной звуковой связи, пеленгации и локации. Гидролокатор, подобно нашей струне, посылает в подводное царство звуковые волны и внимательно «слушает», когда и откуда вернется эхо. Своеобразным гидролокатором является широко распространенный прибор – эхолот. Улавливая отраженный от дна звук, он определяет глубину водоема. Эхолот используют также для обнаружения косяков рыбы.

Другой прибор – гидроакустический пеленгатор – только «слушает». Он обнаруживает на большом расстоянии невидимый источник подводного звука – например, работающий корабельный двигатель. Существуют и подводные звуковые маяки, по сигналам которых капитаны могут вести свои корабли.

Вы можете и сами понаблюдать, насколько хорошо вода проводит звуковые волны. Когда будете нырять в реке или в море, прислушайтесь к подводным звукам. Вы услышите, как у берега волна играет камешками, услышите, как стучит двигатель проходящего вдали парохода.

Легко убедиться и в том, что звук хорошо распространяется в твердых телах. Приложив ухо к железнодорожному рельсу, можно услышать шум приближающегося поезда задолго до его появления, когда звуки, идущие по воздуху, еще совсем не слышны. Подобным образом интересно послушать и водопроводную трубу – она может «донести» до вас много далеких шумов.

В технике широко используют специальные приборы – акустические дефектоскопы, которые следят за тем, как проходит звук по твердому телу. С их помощью удается обнаружить невидимый дефект в ответственной детали, например раковину в стальном вале электрогенератора или трещину в бетонном фундаменте будущего дома.

Можно рассказать много интересного о свойствах звуковых волн, о том, как акустика помогает самым различным областям науки и техники, о новых акустических приборах. Однако пора возвращаться к своей главной задаче – к знакомству с характеристиками звуковых колебаний. Сейчас предстоит познакомиться с еще одной характеристикой, еще одним и, кстати говоря, исключительно важным понятием. Имя ему – спектр.

Для начала поясним, почему мы назвали спектр «исключительно важным» понятием. Представьте себе, что несколько музыкантов, например, пианист, скрипач, баянист и трубач, взяли на своих инструментах одну и ту же ноту. Забегая немного вперед, скажем, что при этом все четыре инструмента создают звуковые волны с одним и тем же периодом. Можно рассадить музыкантов так, что в определенной точке все четыре звуковые волны будут создавать и одинаковое давление. Но никаким способом не удастся добиться, чтобы звуки, идущие от разных инструментов, были неотличимо похожи друг на друга. Вы прекрасно знаете, что скрипка и труба всегда звучат по‑разному даже тогда, когда берут одну и ту же ноту.

Чем же отличаются, казалось бы, одинаковые звуки, исходящие из разных инструментов? Они отличаются пока еще загадочным для нас спектром.

Очень часто учебная модель какого‑либо прибора или аппарата устроена намного проще оригинала. Делают это для того, чтобы сразу не запугивать ученика и сложность реальной техники раскрывать перед ним постепенно. Исходя из подобных побуждений, и мы выбрали для первого знакомства чрезвычайно упрощенный образец звуковых колебаний (рис. 1 и 4). В основном, было сделано два упрощения, два отклонения от истины, и, пожалуй, сейчас можно честно рассказать о каждом из них.

На рис. 5 приведено несколько графиков реальных звуков. Во многом все они похожи: имеют одинаковый период колебаний, одинаковую амплитуду. В то же время сразу видно, что все эти звуки сильно отличаются один от другого и от «учебного» (рис. 1 и 4). Они отличаются формой кривой. А за этими, казалось бы, сухими словами «форма кривой» скрывается очень многое – весь ход изменения звукового давления. Вы видите, что в одном случае (рис. 5, а) звуковое давление изменяется очень неуверенно – в течение каждого полупериода оно несколько раз становится то больше, то меньше. Второй график (рис. 5, б) показывает, что сжатие и разрежение существует лишь небольшую часть периода, а все остальное время звуковое давление близко к нулю. Совсем иначе проходят колебания в третьем случае (рис. 5, в). Здесь звуковое давление почти весь период действует с наибольшей амплитудной силой.

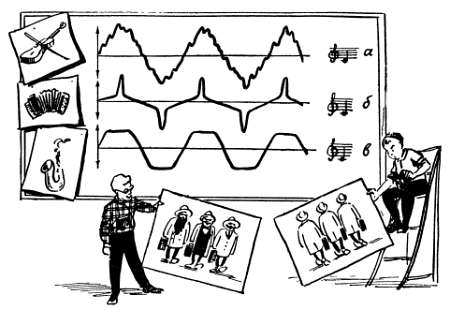
Рис. 5. Одинаковые по высоте (частоте) звуки, исполненные на различных музыкальных инструментах, звучат по‑разному. Характер звучания определяется формой кривой (спектром).

Кроме уже знакомой струны, существует огромное множество источников звука, которые создают самые разнообразные звуковые колебания с самой причудливой формой кривой.

Наше ухо, а мы его назвали главным потребителем звуковых волн, довольно точно различает все эти звуки. Иными словами, ухо каким‑то образом оценивает не только силу, не только частоту звука, но и форму кривой его графика.

Из всего сказанного придется сделать невеселый вывод. Путешествуя по зоопарку, мы не заметили слона; изучая звуковые колебания, не ввели очень важный для них параметр – форму кривой. Но как только захотим исправить эту ошибку, то сразу же столкнемся с серьезными, на первый взгляд даже непреодолимыми трудностями. Как можно точно оценить форму графика? В каких единицах ее измерять? Как сравнивать разные по форме кривые, отмечать их сходство или различие?

Для начала попробуем решить подобную задачу из другой области. Представьте себе, что вам нужно, пользуясь картой, измерить площадь какого‑либо водоема, например Черного моря. В этом случае можно поступить так: разбить всю поверхность моря на квадраты, посчитать площадь каждого из них, а затем все полученные результаты сложить. При этом на карте разместятся два‑три больших квадрата, несколько квадратов поменьше и, наконец, множество мелких и мельчайших квадратиков, которые точно воспроизведут сложные очертания морских берегов (рис. 6).

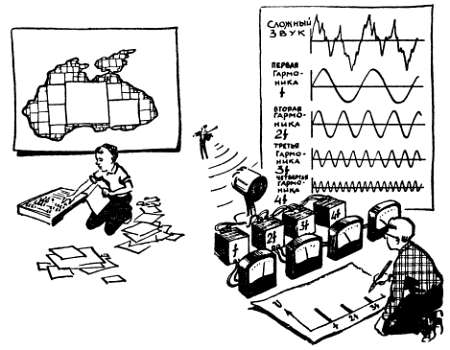
Рис. 6. Звук сложной формы можно представить в виде суммы простейших синусоидальных составляющих (гармоник) с разными частотами и амплитудами. Такой набор синусоидальных составляющих называется спектром сложного звука.

Подобным же образом для оценки формы кривой какого‑либо звука его можно представить как сумму каких‑то составляющих– звуков с разными амплитудами, частотами и фазами, но с одинаковой стандартной формой кривой. В этом случае сравнительно просто описать форму графика любого, самого сложного звука. Нужно лишь назвать набор стандартных составляющих, которые в сумме дадут этот сложный звук.

То, что сложную геометрическую фигуру можно представить в виде суммы более простых фигур, в частности квадратов, ясно и без особых рассуждений. А вот можно ли подобную операцию суммирования производить со звуковыми колебаниями? Оказывается, можно.

Если в точку, где расположен измеритель звукового давления, направить две звуковые волны, то прибор не будет в отдельности реагировать на каждую из них, а покажет суммарное давление. Это как раз и означает, что для получения звуковых колебаний сложной формы достаточно сложить, то есть заставить совместно работать, определенный набор простых по форме звуков. И наоборот, всякий сложный звук можно разложить на более простые составляющие.

Пока слово «можно» мы применили условно, имея в виду «в принципе можно». Однако в дальнейшем вы познакомитесь с приборами, которые без всяких условностей, в буквальном смысле слова могут разложить сложный звук на набор простых составляющих. Кстати, один из таких приборов – это наше ухо.

Из чего же нужно исходить при выборе стандартной составляющей для разложения сложных звуков? Какому из многочисленных простых графиков здесь следует отдать предпочтение?

Решать эти вопросы нам уже не придется – составляющая, наиболее удобная для разложения сложных колебаний, в том числе и сложных звуков, уже выбрана.

Выбор пал на простейшую кривую, известную под названием «синусоида». Примером синусоидальных (иногда говорят, гармонических) колебаний может служить «учебный» звук, а его график (рис. 4), так же как и график колебаний «учебной» струны и маятника (рис. 1 и 3), представляет собой типичную синусоиду. Чем же привлекла к себе внимание эта кривая?

Прежде всего нужно сказать, что синусоиду выбрала сама природа. Природа создала прибор – ухо животных и человека, которое может выделять из сложного звука простейшие составляющие, причем именно синусоидальные. Синусоида – очень популярная кривая. Графики бесчисленного множества различных колебаний – электрических, механических, световых, молекулярных, химических – имеют вид синусоиды или, во всяком случае, очень ее напоминают. Ну, и в заключение отметим, что, по‑видимому, нужно было сказать в самом начале. Синусоида обладает рядом замечательных математических свойств, благодаря которым природа «считает» самым естественным, самым удобным, самым простым видом колебаний именно синусоидальные.

Итак, будем считать, что выбор сделан. Теперь, чтобы описать форму кривой сложного звука, достаточно указать эквивалентный ему набор синусоидальных колебаний, который называется спектром сложного звука. Спектр принято изображать в виде особого графика, напоминающего частокол (рис. 6). Из этого графика сразу же видно, каковы частоты отдельных составляющих и какую амплитуду имеет каждая из них.

В начале XIX века французский математик Жан Батист Жозеф Фурье предложил формулы, по которым можно вычислить амплитуды всех синусоидальных составляющих сложного звука. Одновременно было доказано: если рисунок на графике сложного звука периодически повторяется, то в спектре наверняка будут гармоники – синусоидальные (гармонические) составляющие с частотами, кратными основной частоте, то есть частоте сложного звука. Так, например, если основная частота f = 100 гц, то в спектре будут составляющие с частотами 100 гц (первая гармоника, частота f ), 200 гц (вторая гармоника, частота 2f ), 300 гц (третья гармоника, частота 3f ) и т. д. Как правило, чем выше номер гармоники, тем меньше ее амплитуда. Математическое описание спектра, составленного из гармоник, носит название «ряд Фурье».

Потом мы в основном будем иметь дело с периодическими звуками, спектр которых состоит только из гармоник. Если же в спектр, кроме гармоник, придется вводить еще какую‑нибудь составляющую, то мы будем считать, что это «ЧП» – чрезвычайное происшествие, и сразу же обратим на него внимание.

Научившись с помощью спектра – набора гармоник – точно описывать форму сложной кривой, мы в какой‑то мере исправили первое упрощение, сделанное при знакомстве с «учебной» струной. Струна не создает синусоидальные колебания, как это показано на рис. 1, и спектр колебаний реальной струны содержит целый ряд гармоник (рис. 6).

Знакомясь с колебаниями струны, мы сделали еще одно упрощение, и его также следует исправить. Для этого достаточно сильней натянуть «учебную» струну, чтобы в несколько раз повысить частоту ее колебаний. Без этого колебания воздуха, которые создает струна, вообще нельзя будет считать звуком. Почему?

Как видно из графиков, период колебаний в нашем примере составляет 0,1 сек, а значит, частота равна 10 гц. В то же время ухо воспринимает акустические колебания с частотами от 16 гц до 22 кгц. Слышимым звуком можно называть только те колебания, которые укладываются в этот диапазон. Неслышимые акустические колебания с частотой ниже 16 гц называют инфразвуком, а выше 22 кгц – ультразвуком.

Более подробно об этом будет рассказано в следующем разделе, который в основном посвящен замечательному творению живой природы – органу слуха.

«Я вас слушаю!..»

Когда вы отвечаете на телефонный звонок или просто обращаетесь к собеседнику, то не задумываетесь о том, что стоит за простым выражением: «Я вас слушаю». За этими словами скрывается очень многое: тончайшие и во многом загадочные химические реакции, работа сложных, до сих пор не понятых инженерами физических приборов и вычислительных машин, о которых современная кибернетика пока только мечтает. Еще стоят за этими словами поражения и победы, борьба за право жить на Земле, полная драматизма бурная история, которая рассказывает о событиях, происходивших сотни миллионов лет назад.

Геологическая химия установила, что возраст Земли составляет примерно 5,3 миллиарда лет и что жизнь зародилась на нашей планете около миллиарда лет назад.

Миллиард лет – это очень большой срок. За это время можно было бы 300 миллионов раз пешком обойти вокруг земного шара или 15 миллионов раз «сходить» на Луну и обратно. За это же время обычным стаканом можно 200 раз вычерпать всю воду из Азовского моря. А если каждый день сбрасывать у своего дома хотя бы несколько десятков лопат земли, то через миллиард лет по соседству с вами появится гора, значительно более высокая, чем Эльбрус. Вот что такое миллиард лет.

И все же этот срок не кажется очень большим, когда вспоминаешь, как много он должен был вместить событий, связанных с развитием живой природы.

Сейчас на Земле найдено и описано более 500 тысяч видов растений и 1100 тысяч видов животных и насекомых, в том числе 50 тысяч видов позвоночных животных. Все это изумительное многообразие берет свое начало от простейших одноклеточных организмов, а может быть, даже от какого‑нибудь одного типа самых примитивных живых клеток. Неутомимый мастер – природа усложняла простейшие клетки, создавала клеточные коллективы‑организмы, прилаживала их к условиям окружающей среды, отбраковывала слабые и плохо приспособленные образцы. Природа закрепляла наиболее важные, полезные свойства и способности, повышала квалификацию отдельных клеток и формировала из клеток‑специалистов органы особого назначения, такие, как плавник или крыло, глаз или сердце. Из поколения в поколение совершенствовался мир живого, управляемый железными законами изменчивости, наследственности и естественного отбора. В результате титанической, ни на секунду не прекращавшейся работы природа за миллиард лет создала такие шедевры, как организм человека, состоящий из 20 триллионов невидимых химических комбинатов – четко взаимодействующих живых клеток.

Растения развивались в сравнительно спокойной обстановке. Они прямо на месте получали все необходимое для жизни: от солнечных лучей – энергию, из почвы – строительный материал, разнообразные минеральные вещества, из дождевого облака – влагу. И поэтому, как ни совершенствовались растения, приспосабливаясь к морям и пустыням, зною и холоду, они так навсегда и остались неподвижными.

Другое дело животные. Они должны были сами искать для себя пищу и при этом еще не стать пищей какого‑нибудь более сильного «коллеги». Вот почему в животном мире, начиная с его простейших представителей, выживало и развивалось то, что могло хорошо двигаться и ориентироваться.

Вот почему у животных до такой высокой степени развились органы движения и нервная система.

Нервная система – это сложный орган, а точнее, целый комплекс взаимосвязанных органов, с помощью которого организм изучает окружающий мир, непрерывно оценивает обстановку и на основе этого организует свое поведение. Развитие нервной системы и особенно ее главного штаба – головного мозга – в итоге оказалось решающим фактором в борьбе за существование, за прогресс того или иного вида животных.

Сбор информации об окружающем мире организм осуществляет с помощью рецепторов. Это специализированные клетки (Иван Петрович Павлов называл их клетками‑осведомителями), которые под действием света, тепла, давления или химических веществ посылают определенные сигналы в нервную систему. Некоторые рецепторы появились на довольно ранних стадиях развития живого организма. Так, в частности, приемники света, фоторецепторы, разбросаны по всему телу дождевого червя, представителя древнейшего типа животных– кишечнополостных. Некоторое подобие фоторецепторов встречается даже у одноклеточных. У сложных животных рецепторные клетки объединяются в целые органы, такие, как глаз (знаете ли вы, что глаз человека содержит около 200 миллионов светочувствительных клеток?), органы обоняния и вкуса.

Рецепторы звуковых колебаний, а значит, и орган слуха появились намного позже других, так как острая необходимость в них возникла сравнительно недавно, «всего» 150–200 миллионов лет назад. К этому времени наиболее смелые представители подводного мира (а жизнь, как известно, зародилась и развивалась в океане), стали выбираться на берег, постепенно превращаясь в сухопутных животных.

В земных условиях звуковые волны приносят исключительно важные «сообщения» – журчание ручья, шаги приближающегося хищника, шорохи убегающей «пищи». Необходимость пользоваться этой информацией и привела к появлению и развитию слуха.

Слуховой аппарат развился из так называемой боковой линии рыб – своеобразного органа давления, точнее, цепочки органов, вытянувшихся от головы до хвоста по обеим сторонам рыбьего тела. Боковая линия реагирует на медленные изменения давления, позволяет рыбам огибать препятствия, чувствовать приближение других рыб и даже «слышать» некоторые звуки. В частности, установлено, что рыба голец слышит звуки с частотой до 3 кгц, гольян – до 7 кгц и сомик – до 12,4 кгц. В последнее время проведено много интересных опытов, в которых рыб приучали реагировать на различные звуки: например, двигаться за пищей, ориентируясь на источник звуковых волн.

Но услышать звук – это еще далеко не все, нужно проанализировать его, отличить одни звуки от других. Таким анализом занимается мозг, и именно от его развития в огромной степени зависит совершенство всего слухового аппарата.

Так у рыб наблюдаются простейшие реакции на звук – обычно они просто бегут от источника звуковых колебаний. Животные амфибии уже умеют выделять некоторые особо важные для них звуковые комплексы, еще лучше развит слух у птиц, и. наконец, у млекопитающих, к классу которых относимся и мы с вами, слуховой аппарат достигает высочайшей степени совершенства, становится одним из главных средств сбора информации об окружающем мире.

Слуховой аппарат человека можно условно разделить на три основные части (рис. 7, 5, б ).

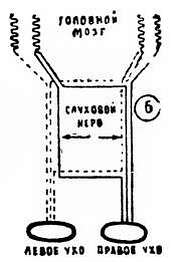
рис. 7 , 5, б

1. Ухо принимает звуковые колебания и предварительно сортирует их по частоте и по мощности. Здесь же составляется и отправляется в мозг шифрованная «телеграмма», формируются серии сложных электрохимических сигналов – нервных импульсов, которые несут подробное описание принятого звука.

2. Анализ нервных импульсов, то есть фактически анализ звука, осуществляют специально для этого приспособившиеся участки коры головного мозга, расположенные в височных частях обоих больших полушарий. Левый и правый слуховые участки сложным образом связаны, и звук, принятый, например, правым ухом, попадает не только в «свое», но и в левое полушарие. Сопоставляя сигналы, принятые правым и левым ухом, мозг вычисляет место расположения источника звуковых волн. Интересно, что звуки разных частот изучаются в разных районах слуховых участков мозга, а если раздражать эти участки слабым электрическим током, то у человека возникает ощущение услышанного звука.

3. Третьим элементом слухового аппарата можно считать линию связи ухо – мозг, основа которой – слуховой нерв – состоит из многих тысяч нервных волокон. На этой линии имеется несколько промежуточных узлов связи, где, по‑видимому, происходит предварительная обработка нервных импульсов, идущих в мозг.

Из всех элементов слухового аппарата для нас сейчас наибольший интерес представляет само ухо, и с ним мы познакомимся несколько подробнее.

Всякий, кому приходилось бывать в метро, знает, что наземная станция – это лишь небольшая часть всего сооружения и что самое главное – прекрасные дворцы, могучие машины, бесконечные туннели – находится под землей. Подобно этому орган, который мы привыкли называть ухом, – это лишь своего рода наземная станция, получившая название «наружное (внешнее) ухо» (рис. 7, 5, а ). Главные же части нашего звукоприемника – среднее и внутреннее ухо – нам не видны. Они спрятаны довольно глубоко и защищены костями черепа.

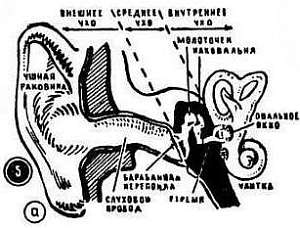
рис. 7 , 5, а

Звуковые волны, попавшие в ушную раковину, пробегают через извилистый слуховой проход (его длина около 2,5 см) и приводят в движение барабанную перепонку. Она, в свою очередь, связана с системой миниатюрных косточек – молоточком, наковальней и стремечком, которые все вместе весят около 0,05 г. Слуховые косточки расположены так, что образуют рычаг – своего рода усилитель. Конец этого рычага раскачивает барабанная перепонка, а на другом конце получаются колебания с меньшей амплитудой, но зато действующие с большей силой. Эти колебания попадают в самый главный «цех» внутреннего уха – в улитку. Название «улитка» этот орган получил потому, что у млекопитающих он действительно похож на спиралевидный домик улитки. У животных, которые стоят на более низкой ступени развития, в частности у птиц, улитки еще нет, ее место занимает более простой орган, немного похожий на изогнутую луковицу.

Улитку внутреннего уха человека удобно представить себе как постепенно сужающуюся трубку длиной около 3 см и закрученную в спираль на три, точнее, на 2^3/4 витка.

Итак, улитке передаются звуковые колебания от слуховых косточек. Наряду с этим к ней подходят нервные волокна, связанные со слуховым нервом. Отсюда можно сделать только один вывод: именно в улитке находятся звукорецепторы, находится орган, преобразующий звуковые колебания в серии нервных импульсов. Этот орган, по имени одного из его первых исследователей – А. Корти, получил название кортиева органа (орган Корти).

Кортиев орган надежно укрыт – он находится в спиральном лабиринте улитки (рис. 7, 5, г , поперечный разрез витка улитки) и чем‑то напоминает плоский и длинный слоеный пирог, также закрученный в спираль.

Нижний слой, основание «пирога», – лента основной мембраны, сотканная из 25 тысяч поперечных тонких нитей. Эти нити часто сравнивают со струнами рояля или арфы. В направлении от основания улитки к ее вершине основная мембрана расширяется, и нити‑струны становятся длиннее. У основания улитки (овальное окно), куда примыкает третья слуховая косточка – стремечко, длина нитей составляет 100 мк, а у вершины улитки – 500 мк (рис. 7, 5, в ).

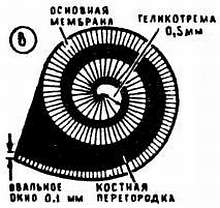
рис. 7 , 5, в

На основной мембране расположились ткани из нескольких типов клеток. В самом наружном слое имеется пять рядов так называемых волосковых клеток (кончик каждой из них покрыт десятками тончайших волосков), к которым подходят нервные волокна (рис. 7, 5, д ).

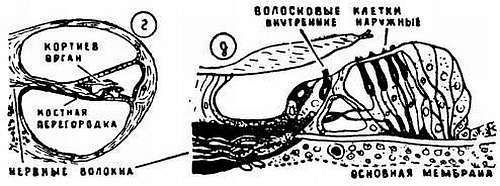
рис. 7 , 5, д

Изучение устройства и работы слухового аппарата началось давно, но еще сегодня в этой области существует очень много загадок. Так до сих пор не удалось проследить все стадии преобразования звука в нервный импульс. Неясно также, каким образом кортиев орган анализирует форму кривой звука, как разделяет сложный звук на синусоидальные составляющие. Существует несколько теорий слуха, но, пожалуй, ни одна из них полностью не объясняет принцип действия нашего звукоприемника.

Долгое время широким признанием пользовалась так называемая резонансная теория слуха, которую около ста лет назад разработал известный физик и врач Герман Гельмгольц. Как говорит само название, в основе этой теории лежит хорошо известное явление – резонанс.

Существует много опытов для иллюстрации резонанса, но один из этих опытов особенно хорошо поясняет резонансную теорию слуха. Откройте крышку рояля или пианино, нажмите правую педаль и с большими паузами спойте над струнами несколько коротких звуков. Вы услышите, как рояль вторит пению, причем после разных нот звучат и разные струны.

Происходит это потому, что каждая струна в основном резонирует лишь на одну из синусоидальных составляющих сложного звука. Поэтому для различных сложных звуков, то есть для разных спектров, набор откликающихся струн оказывается различным.

Гельмгольц считал, что наш слуховой аппарат определяет спектр сложных звуков примерно таким же способом. Роль резонирующих струн он отводил нитям основной мембраны, которые имеют разную длину, а значит, и разную частоту резонанса. Эксперименты, казалось бы, полностью подтверждали резонансную теорию слуха. Так, например, при повреждении вершины улитки, где находятся сравнительно длинные низкочастотные волокна, подопытные животные теряют слух в области низших частот, а повреждение основания улитки приводит к потере слуха на высших частотах. В пользу резонансной теории говорили и многие другие эксперименты.

И все же под давлением фактов, особенно полученных в самое последнее время, от простой и, казалось бы, понятной модели уха‑рояля пришлось отказаться. Вот лишь одно из затруднений резонансной теории. Простейшие расчеты показывают, что для того, чтобы перекрыть весь диапазон слышимых частот (16 гц– 22 кгц), сила натяжения крайних «струн» должна отличаться в 10 тысяч раз. О такой большой разнице не может быть и речи. Для «струн» из живой ткани она недопустима.

Сейчас главное внимание исследователей приковано к волосковым клеткам, где звук преобразуется в нервный сигнал. Установлено, что этот процесс включает в себя целые комплексы химических реакций, с которыми, по‑видимому, связано и разделение сложного звука на составляющие. Обнаружены интересные особенности поведения некоторых частей волосковой клетки при воздействии различных звуков. Одним словом, стало ясно, что важнейшие проблемы слуха нужно рассматривать с позиций молекулярной биологии, которая исследует самые тонкие биологические механизмы.

Изумительная биологическая машина

Несмотря на неясности в работе слухового аппарата, его главные характеристики изучены весьма подробно. Так, в частности, установлена чувствительность, или, иначе, порог слышимости, уха – сила самых тихих звуков, которые мы еще в состоянии услышать. Оказалось, что на разных частотах порог слышимости различен, и лучше всего мы слышим звуки с частотами от 1 до 5 кгц. На краях диапазона слышимых звуков чувствительность уха резко – во много миллионов раз – падает.

Сила звука на пороге слышимости (для частоты 1000 гц) составляет около 10^‑12 вт/м², а звуковое давление – 0,00002 н/м². Под действием таких слабых звуков давление на барабанную перепонку не превышает 0,0000003 г, и амплитуда ее колебаний измеряется тысячными долями микрона. Амплитуда звуковых колебаний на входе улитки еще в 50–60 раз меньше, а размах колебаний основной мембраны оказывается в несколько раз меньше, чем диаметр атома водорода. Уже одно это говорит о том, какие сложные и тонкие процессы обеспечивают высокую чувствительность уха.

Самые громкие звуки, которые мы можем слышать, называют порогом болевых ощущений. Он соответствует силе звука около 10 вт/м² и давлению около 65 н/м². За этим порогом ухо действительно ощущает боль и громкость звука становится невыносимой. Для сравнения заметим, что чувствительные окончания кожи ощущают прикосновение уже при давлении 6 н/м². Порог болевых ощущений неодинаков на разных частотах, хотя и меняется не так резко, как порог слышимости. Значение обоих порогов для разных частот вы найдете на графике (рис. 7, 1 ).

Области «речь» и «симфонический оркестр» показывают, в каких пределах находятся частоты и звуковые давления для этих источников звука. В табл. 2 указаны некоторые источники звуковых колебаний и соответствующие им звуки различной силы.

Приведенные цифры показывают, что ухо слышит звуки в огромном диапазоне громкостей. Самый сильный и самый слабый из слышимых звуков могут различаться по звуковому давлению в 3 миллиона раз, а это соответствует разнице силы звука в 10 триллионов раз! Измеритель длины с подобным диапазоном мог бы одинаково хорошо определить толщину человеческого волоса и расстояние до Луны. Этот, конечно, весьма условный пример в какой‑то степени характеризует универсальность слуха, его способность воспринимать самые различные звуки.

Вас, наверное, интересует, с какой точностью ухо ориентируется в огромном диапазоне звуков различной громкости, из скольких ступенек состоит лестница, которая ведет от самого тихого к самому громкому звуку, от порога слышимости к порогу болевых ощущений. В качестве ответа можно привести результаты, полученные многими исследователями. Человек различает около четырехсот (точнее, 374) ступенек – звуков различной громкости. Но сама по себе эта цифра еще мало о чем говорит – она нуждается в целом ряде пояснений и дополнений. Вот некоторые из них.

Во‑первых, речь идет об оценке громкости путем сравнения двух разных звуков. Если оценивать звуки поодиночке, то удается заметить значительно меньше ступенек (часто говорят: градаций) громкости.

Во‑вторых, заметим, что приведенная цифра получена в результате проверки слуха у большого числа людей и относится к так называемому среднему человеку. Люди с натренированным слухом, например опытные музыканты, по‑видимому, могут заметить меньшие интервалы громкости, и, таким образом, для них число ступенек окажется намного больше.

В‑третьих, приведенная цифра относится лишь к средним частотам, например к частоте 1000 гц. С повышением и понижением частоты мы намного хуже различаем звуки разной громкости. Так, например, на частотах 150 гц и 9 кгц можно заметить лишь около ста, на частоте 16 кгц – меньше двадцати, а на частоте 30 гц – всего три различных ступеньки, различных уровня громкости.

В‑четвертых, способность различать разные звуки в большой степени зависит от того, насколько мы к ним привыкли. Есть данные о том, что через 20 мин высота ступеньки – заметный интервал громкости – уменьшается в 1,35 раза, а через 2 часа – почти в 3,5 раза. Подобное явление – адаптация– наблюдается и у других органов чувств: всем хорошо известно, что наши глаза постепенно привыкают к темноте и видят то, что в первый момент было совершенно неразличимым.

В‑пятых, высота ступенек увеличивается с высотой лестницы. По мере повышения силы звука ухо как бы грубеет: чтобы оно заметило изменение громкости, приходится резче менять звуковое давление. На этом свойстве стоит остановиться подробнее, так как в дальнейшем мы не раз будем его учитывать.

Совершенно ясно, что ощущение громкости прежде всего зависит от звукового давления на барабанную перепонку – чем больше это давление, тем более громким кажется звук. Ну, а насколько повышается громкость, если повысить звуковое давление на единицу, например на 1 н/м², или увеличить силу звука на 1 вт/м²? Оказывается, что на вопрос, поставленный подобным образом, ответить невозможно. Если вас кто‑нибудь спросит, много это или мало 1 л воды, то вы наверняка прежде всего захотите узнать, в сравнении с чем «много или мало». Действительно, если добавить литр воды в неполное ведро, то это сразу же станет заметным, и, конечно, вы ничего не заметите, если дольете литр воды в море.

Наш простой пример в какой‑то степени помогает понять важнейший закон физиологии – закон Вебера – Фехнера. Названный именами открывших его ученых – физиолога и математика, этот закон говорит о том, что органы чувств – глаз, ухо – всегда замечают одинаковый прирост какого‑либо воздействия (яркость картинки, сила звука), но прирост, одинаковый не по абсолютной, а по относительной величине, прирост не «на столько‑то» единиц, а «во столько‑то раз» или «на столько‑то процентов». Чтобы заметить изменение громкости, нужно увеличить силу звука примерно на 10 %: если было 0,2 н/м², добавить еще 0,02 н/м²; если было 20 н/м², добавить 2 н/м². Одним словом, в ведре заметен лишний литр воды, в цистерне – лишняя бочка.

Для иллюстрации закона Вебера – Фехнера построим график (рис. 7, 4 и рис. 8), который покажет, как изменяется уровень громкости (разумеется, это условная величина, оценка наших ощущений, выраженная в условных единицах) при изменении силы звука.

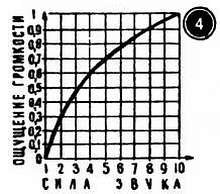
рис. 7 , 4

Рис. 8. Зависимость между ощущением громкости и звуковым давлением носит логарифмический характер (закон Вебера – Фехнера ). Чтобы повысить громкость и без того громкого звука, нужно увеличить звуковое давление на весьма значительную величину.

Кривая, которую вы видите на этом графике, называется логарифмической – такая же по форме кривая показывает, как меняется значение логарифма по мере увеличения числа, к которому этот логарифм относится (рис. 7, 3 ). Отмеченное сходство не случайно. Путем ряда математических преобразований можно прийти к такой формулировке закона Вебера – Фехнера: «Ощущение пропорционально логарифму раздражения».

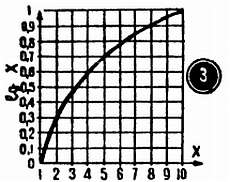
Поскольку зависимость между громкостью (ощущение) и звуковым давлением (раздражение) носит логарифмический характер, для оценки этих величин особенно удобно пользоваться самыми популярными единицами – децибелами.

Строго говоря, децибел не имеет никакого отношения ни к ваттам, ни к вольтам, ни к ньютонам. И в то же время с помощью этой единицы оценивают величину мощности и напряжения, тока и звукового давления, силы звука и электрического сопротивления. Децибел, «невзирая на лица», сравнивает две величины, например два напряжения или два звуковых давления, и показывает, во сколько раз одна из них больше другой. Вот поэтому‑то децибелом пользуются всякий раз, когда нужен беспристрастный судья, когда нужно оценить относительное усиление, ослабление, рост, уменьшение, подъем, – одним словом, любое отличие или изменение независимо от того, что именно меняется.

Мы коротко рассказали, для чего нужен децибел, и уже, по‑видимому, настал момент пояснить, что он собой представляет. Для этого прежде всего вспомним, что такое логарифм и, в частности, десятичный логарифм.

Любое число можно представить как число 10, возведенное в определенную степень. Вот несколько примеров: 100 = 10²; 1 000000 = 10⁶; 2=10^0,3. В данном случае показатель степени это и есть десятичный логарифм числа. Логарифмы приведенных чисел соответственно равны 2; 6 и 0,3. Сокращенно это записывают так:

lg 100 = 2; lg 1000000 = 6; lg 2 = 0,3.

Значение логарифма того или иного числа можно найти по графику или в специальной таблице. Таблицы и графики позволяют по значению логарифма определить и само число.

Довольно подробно о логарифмах и операциях с ними рассказано в учебнике алгебры для 10‑го класса. Мы же буквально в двух словах скажем о тех операциях, с которыми в дальнейшем придется встретиться в этой книге.

Вот пример того, как с помощью логарифмов можно выразить отношение двух величин. Если есть два звука разной силы: один 0,05 вт/м², а другой 5 вт/м², то сразу же можно сказать, что второй звук сильнее первого в 100 раз. Можно сказать и иначе: логарифм отношения силы этих звуков равен двум (lg 100 = 2).

Сравнивая две величины, мы пользуемся своего рода единицей сравнения, которую можно было бы назвать «раз». Мы так и говорим: «сильнее в 100 раз», «слабее в 3 раза», «увеличился в миллион раз» и т. д. Когда результат сравнения выражают в виде логарифма, то единицей служит «бел», который соответствует логарифму числа 10, то есть единице. Так, в нашем примере можно сказать, что второй звук сильнее первого на две логарифмические единицы, то есть на 2 бела.

Обычно на практике пользуются более мелкой и поэтому более удобной единицей – децибелом . Из самого слова понятно, что децибел (сокращенно db или дб ) составляет 0,1 часть бела (сравните с дециметром, который равен 0,1 м). В дальнейшем мы будем очень широко пользоваться децибелом, и вы постепенно привыкнете к этой единице. Ее «удельный вес» вам поможет понять табл. 3.

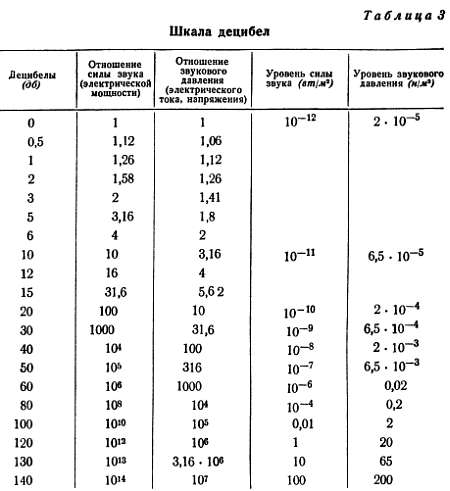
В первой (левой) колонке этой таблицы помещены некоторые наиболее часто встречаемые числа децибелов. В следующей, второй колонке приведены отношения (число раз) силы звука, соответствующие тому или иному числу децибелов. Сразу видно, что наш пример, где сила двух звуков отличалась в 100 раз, соответствует разнице в 20 дб (2 бела).

Если бы один звук был сильнее другого в миллион (10⁶) раз, то мы сказали бы, что они отличаются на 60 дб. Если различие в силе звуков составляет 3 дб, то это значит, что один из них сильнее другого в два раза. В дальнейшем первой и второй колонками табл. 3 мы будем пользоваться для того, чтобы переводить в децибелы не только соотношения силы звука, но и соотношения электрической мощности, энергии, выполненной работы.

Некоторое недоумение у вас, по‑видимому, вызовет третья колонка табл. 3. Здесь для того или иного числа децибелов (первая колонка) приведены соотношения звукового давления. Странным на первый взгляд кажется, что одному и тому же числу децибелов соответствуют разные соотношения силы звука и звукового давления. При 20 дб сила звука отличается в 100 раз, а звуковое давление только в 10 раз. Разница силы звука в два раза – это 3 дб, а такая же разница звуковых давлений – это уже б дб.

Сейчас мы попытаемся ликвидировать эту неясность.

Сила звука и звуковое давление – это взаимно связанные величины, подобно тому, как связаны между собой площадь квадрата и длина его стороны. Ни одна из этих величин не может измениться так, чтобы другая осталась неизменной. Без особых доказательств ясно, что если увеличить сторону квадрата в два раза, то площадь его возрастет в четыре раза, увеличим площадь в девять раз, и сторона станет длиннее в три раза. Подобная зависимость – она называется квадратичной– существует также между звуковым давлением и силой звука. Если звуковое давление увеличится в три раза, то сила звука обязательно возрастет в девять раз. Если сила звука повышается в 100 раз, то, значит, звуковое давление возросло в 10 раз. Вот почему в табл. 3 в одном горизонтальном ряду, то есть для одного и того же числа децибелов, приводятся соотношения и для силы звука, и для звукового давления, причем соотношения, связанные квадратичной зависимостью.

Кстати, зная одно из этих соотношений, всегда легко получить второе: звуковое давление нужно возвести в квадрат, а из силы звука извлечь квадратный корень. Путем подобных вычислений и построена третья колонка табл. 3.

Квадратичная зависимость связывает не только силу звука и звуковое давление. Такой же зависимостью связаны и многие другие величины, в частности электрическая мощность с величиной тока и электрическая мощность с величиной напряжения. Поэтому, для того чтобы перевести в децибелы соотношение токов или напряжений, нужно пользоваться третьей колонкой табл. 3,

В свое время мы назвали децибел самой популярной единицей, и вы уже, по‑видимому, поняли, что для этого есть основания. Децибелами широко пользуются электрики, электронщики, радисты. Однако особую популярность эта единица завоевала у специалистов по акустике. Они часто забывают об истинных единицах звукового давления и силы звука и выражают эти величины прямо в децибелах. Чтобы понять, как это делается, нужно сопоставить первую, четвертую и пятую колонки табл. 3.

Самый тихий звук, который мы еще слышим (порог слышимости), соответствует звуковому давлению 0,00002 н/м². Все более громкие звуки будут создаваться давлением, большим в определенное число раз, то есть на определенное число децибелов. Поэтому, приняв 0,00002 н/м² за нулевой уровень давления (меньшее давление для нас действительно равносильно нулю, так как звук не слышен), можно все остальные величины звукового давления выражать прямо в децибелах.

Это и показано в пятой колонке табл. 3. Здесь приведены звуковые давления, соответствующие тому или иному числу децибелов при условии, что отсчет производится от порога слышимости (0 дб). Условившись об этом, мы в дальнейшем будем говорить: «Звуковое давление равно 40 дб» или «звуковое давление поднялось до 80 дб», имея в виду, что эти цифры соответствуют 0,002 н/м² и 0,2 н/м² (пятая колонка табл. 3). Аналогично, приняв за нулевой уровень силу звука на пороге слышимости, мы выражаем в децибелах и эту величину (четвертая колонка табл. 3). Из таблицы видно, что порогу болевых ощущений соответствует примерно 130 дб.

Для того чтобы вы поскорее привыкли к децибелам, мы начнем пользоваться этими единицами, рассказывая об основных характеристиках человеческого слуха.

Прежде всего советуем еще раз взглянуть на табл. 2. Здесь в третьей колонке, на которую вы раньше, по‑видимому, не обратили внимания, приведены уровни громкости (в децибелах) для самых различных источников звука. Громкость в децибелах приводится и на вертикальной оси графика (рис. 7, 1 ), где показано, как меняются с частотой порог слышимости и порог болевых ощущений.

Обратите внимание, что, так же как и на многих других графиках, на графиках рис. 7, 1 и 7, 2 деления горизонтальной шкалы неодинаковы: чем выше частота, тем меньший участок приходится на каждый герц. Эта так называемая логарифмическая шкала вводится для того, чтобы уместить весь диапазон слышимых частот на небольшом участке и в то же время достаточно подробно показать участок средних и особенно низших частот. Логарифмическая шкала как бы приспособлена к особенностям слуха: чем ниже частота, тем меньшие ее изменения мы замечаем. В логарифмическом масштабе размечают не только ось частоты: на некоторых графиках, например, пользуются логарифмической шкалой силы звука.

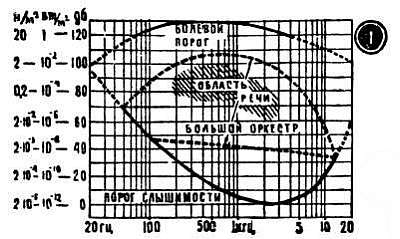
рис. 7 , 1

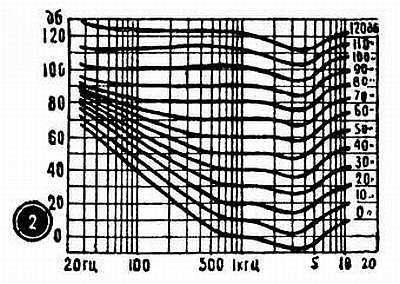
рис. 7 , 2

Из графика рис. 7, 1 хорошо видно, что на средних частотах наше ухо воспринимает огромный диапазон громкостей – около 140 дб. Сравнительно небольшая часть этого диапазона – 40 дб – приходится на разговорную речь. Все многообразие голосов, от самого громкого, крикливого, до самого тихого, едва слышного, лежит в пределах от 60 до 100 дб.

Намного шире диапазон, в который укладывается звучание большого симфонического оркестра. Его высшая точка, 120 дб, соответствует самому громкому звуку – форте‑фортиссимо – всех инструментов. Низшая точка, около 45 дб, соответствует самому тихому – пиано‑пианиссимо – звучанию одной скрипки.

Несколько слов о том, как следует оценивать музыкальные термины «форте» и «пиано». Музыканты ввели для себя восемь уровней громкости и обозначают их так:

ррр– пиано‑пианиссимо

рр – пианиссимо

р– пиано

тр – меццо‑пиано

mf– меццо‑форте

f– форте

ff– фортиссимо

fff– форте‑фортиссимо .

Все эти уровни охватывают диапазон громкости примерно в 70–75 дб и делят его на семь равных частей, по 10 дб в каждой. Музыканты считают, что подъем на одну ступеньку, то есть повышение громкости на 10 дб, создает ощущение удвоенной громкости. Для подъема на одну такую ступеньку, то есть для перехода на следующий уровень громкости, нужно увеличить силу звука в 10 раз, то есть повысить звуковое давление в 100 раз. Из закона Вебера – Фехнера следует, что «ступеньки» по абсолютной величине неодинаковы. При низких уровнях громкости для подъема на 10 дб достаточно увеличить звуковое давление на сотые и даже тысячные доли н/м². В области громких звуков для такого же увеличения громкости (10 дб) приходится повышать звуковое давление на единицы и даже на десятки н/м². Многие музыканты собственными мускулами чувствуют справедливость закона Вебера – Фехнера. Скрипачи, пианисты, барабанщики очень легко переходят от пианиссимо к пиано, но переход от форте к фортиссимо требует от них значительных усилий, в буквальном смысле слова – тяжелой физической работы (рис. 8).

Мы уже отметили, что на частоте 1000 гц человек способен обнаружить около 400 (точнее, 374) различных уровней громкости. Каждой такой ступеньке соответствует изменение силы звука на 0,4 дб, то есть примерно на 10 %. На высших и особенно на низших частотах мы намного хуже различаем громкость звука. В значительной степени это связано с тем, что при понижении частоты резко падает чувствительность уха и вместе с этим как бы сжимается весь диапазон громкости.

Так, на частоте 1000 гц этот диапазон примерно равен 130–140 дб, а на частоте 50 гц всего 80 дб – порог слышимости повышается соответственно от 0 до 50 дб.

Более подробно об этой зависимости рассказывает график на рис. 7, 2 . Здесь изображены так называемые кривые равной громкости, полученные при проверке слуха у большого числа людей. Каждая из этих кривых соответствует определенному уровню громкости, величина которого, разумеется условная, обозначена над кривой. По вертикальной оси отложены уровни силы звука, причем на частоте 1000 гц уровни громкости и силы звука совпадают. Каждая кривая показывает, как с изменением частоты нужно изменить силу звука, чтобы громкость осталась постоянной.

В области низших частот несколько кривых резко загнуты кверху. Это значит, что при уменьшении частоты нужно резко усилить звук, для того чтобы громкость осталась неизменной. Важно отметить, что для громких звуков (от 80 дб и выше) изменение силы звука на всех частотах дает примерно одинаковый эффект. В области слабых звуков (от 80 дб и ниже) даже небольшое уменьшение силы звука на низших частотах приводит к резкому снижению громкости вплоть до самого порога слышимости. Практически это значит, что если каким‑нибудь способом постепенно ослаблять звуки, идущие от большого оркестра или многоголосого хора, то раньше всего мы перестанем слышать низшие частоты.

Можно было бы рассказать еще много интересного о том, как человек воспринимает звуки различной силы, об особенностях оценки громкости. Однако нам уже давно пора перейти к другому важному способу «сортировки» звуковых колебаний, пора рассказать, как мы различаем звуки по их частоте.

Начнем с так называемых простых звуков, график которых представляет собой синусоиду (рис. 1, 2, 4). Принято считать, что человек слышит звуки с частотой от 16 гц до 22 кгц. Однако эти граничные цифры не для всех одинаковы. Большинство взрослых людей не слышат звуки, частота которых выше 16–18 кгц, а для людей преклонного возраста предельная частота может снизиться даже до 10–12 кгц. В то же время встречаются, правда очень редко, и «рекордсмены», которые слышат ультразвук вплоть до 28 и даже до 30 кгц.

Кстати, способность слышать ультразвук хорошо развита у многих животных. Например, собака слышит почти до 40 кгц. Этим пользуются некоторые дрессировщики: с помощью ультразвукового свистка они подают собаке сигналы, не слышимые для зрителей. Есть животные, которые слышат инфразвук – колебания с частотой ниже 16 гц. Советский ученый академик В. В. Шулейкин обнаружил, что ветер, обдувая морские волны, создает «голос моря» – инфразвук с частотой от 0,1 до 6 гц. Из районов, где начался шторм, «голос моря» довольно быстро (звук движется несравненно быстрее морской волны) приходит к берегу. Благодаря этому некоторые моллюски, способные слышать инфразвук, заранее узнают о приближающейся непогоде.

Человеческий слух с исключительно высокой точностью различает частоту звука во всем доступном нам диапазоне. И хотя на самых низких частотах точность несколько падает, она все же остается достаточно высокой. Об этом свидетельствует полученная опытным путем табл. 4, где показано, какое отклонение частоты способен заметить слух среднего человека.

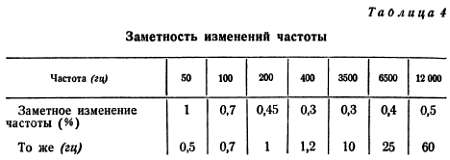
На низших частотах ухо определяет частоту с точностью до 1 %, а начиная с 500 гц и выше, точность возрастает до десятых долей процента. Точность определения частоты в некоторой степени зависит также от громкости звука. Так, при большой громкости (80 дб), в пределах от 16 гц до 22 кгц, человек способен обнаружить около 2200 частотных интервалов – градаций, а при тихом звуке (20 дб) таких интервалов обнаруживается всего около 500, то есть точность определения частоты падает. Табл. 4 соответствует средней громкости (40 дб), при которой мы различаем около 1300 градаций частоты.