Точность формы и ее обозначения
Параметры качества деталей машин
Отклонение параметров детали, при котором она изменяется как геометрическое целое, называется макрогеометрическим или отклонением формы. Различают номинальную и заданную поверхности (рис. 1).
Реальные поверхности – это те поверхности, которые отделяют одно геометрическое тело от другого, то есть ограничивают деталь. В основу нормирования и учета отклонений положен принцип прилегающих поверхностей. Различают понятия прилегающая прямая, прилегающая плоскость, окружность, цилиндр.
Прилегающей плоскостью называется плоскость, проведенная касательно к реальной поверхности и расположенная вне материала детали. Расположена она так, что расстояние от ее наиболее удаленной точки до прилегающей плоскости минимально.

Рис. 1 Реальные и номинальные поверхности деталей
|

Рис. 2 Реальная поверхность (1)
и прилегающая плоскость (2)

Рис. 3 Поверхности детали в продольном и поперечном сечениях
1 – прилегающая плоскость, 2 – реальная поверхность, 3 – номинальная поверхность
Некруглость делится на два отклонения: овальность (рис. 4) и огранка (рис. 5).
Овальность – отклонение формы, при котором деталь представляет из себя овалообразную фигуру, наибольшие и наименьшие диаметры которой примерно взаимно перпендикулярны.
Огранкой называется такое отклонение формы, при котором деталь представляет из себя многогранную фигуру, как правило, с нечетным количеством граней.
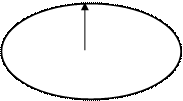
   Dmax
Dmin
ΔOB = Dmax - Dmin Dmax
Dmin
ΔOB = Dmax - Dmin
|
| ||||||
| Рис. 4 Овальность | Рис. 5 Огранка |
Отклонение профиля продольного сечения делится на следующие виды:
1. Конусообразность (рис. 6) – отклонение формы, при котором образующие деталь прямые не параллельны между собой.
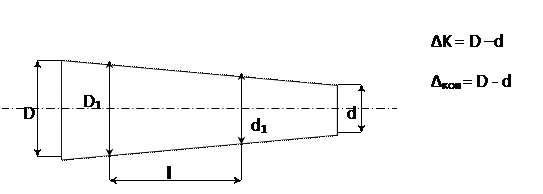
Рис. 6 Конусообразность
2. Бочкообразность (рис. 7) – когда диаметры увеличиваются от краев к середине продольного сечения.
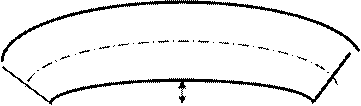
3. Изогнутость оси (рис. 8) – отклонение формы, при которой имеет место непрямолинейность геометрического места центров продольного сечения.
4. Седлообразность (рис. 9) – отклонение формы, у которой диаметры уменьшаются от краев к середине продольного сечения

Рис. 7 Бочкообразность
 |
 ΔИ
ΔИ
Рис. 8 Изогнутость оси









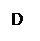
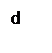

Рис. 9 Седлообразность
Дата добавления: 2016-02-24; просмотров: 695;
