Сущность средних величин
Вариационные ряды отражают большое разнообразие явлений и процессов, составляющих сущность нашей действительности. Для более полного, углубленного их изучения нередко пользуются какой-то одной величиной, которая «впитывает» в себя все особенности данного ряда распределения, основные свойства изучаемой совокупности в отношении определенного признака. Это означает, что для каждого признака статистической совокупности необходимо иметь сводную, сжатую, обобщённую характеристику. Такое возможно при условии, если исчислена средняя величина.
Средняя величина – это обобщенная количественная характеристика признака в статистической совокупности. Она выражает типичное значение признака для всех единиц совокупности под влиянием всего комплекса факторов. В ней погашаются индивидуальные различия единиц совокупности в вариантах осредняемого признака.
Средняя величина – важнейшая категория статистической науки и форма обобщающих показателей. Многие явления и процессы становятся ясными, определенными, лишь будучи обобщенными в форме средних величин. Таковы, например, средняя урожайность, продуктивность животных, производительность труда, себестоимость единицы продукции, заработная плата, душевой доход и т.д.
Основное условие правильного применения средних величин – качественная однородность статистической совокупности. Средние, вычисленные для качественно неоднородной совокупности, теряют свое научное значение. Такие средние являются фиктивными, причем не только не дающими представления о действительности, но искажающими ее и вводящими в заблуждение, так как они стирают существенные различия между явлениями. Например, для характеристики среднего уровня зарплаты в сельскохозяйственной сфере АПК показатель среднего заработка в целом по экономике совершенно непригоден, так как последний в 2-3 раза выше.
Средняя величина независимо от ее вида получает следующее общее выражение:
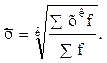 (6.1)
(6.1)
Выражение (6.1) принято называть общей формулой средних величин. При разных значениях к формула (6.1) приводит к разнообразным видам средних величин.
Величина к может принимать любое из бесконечных чисел значение. Именно поэтому для каждого признака теоретически может быть рассчитано бесконечное число видов средних величин. Практически же в статистике находит применение не более десяти видов.
Каждый вид средних величин обычно имеет две формы: простую (невзвешенную) и взвешенную. Форма средних зависит от вида вариационного ряда. Так, при расчете средних по несгруппированным данным применяют простую (невзвешенную) форму; в дискретных или интервальных рядах распределения – взвешенную.
Дата добавления: 2016-02-20; просмотров: 839;
