Квантование энергии. Частица в потенциальной яме
В соответствии со своим смыслом волновая функция 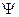 должна быть
должна быть
- однозначной,
- непрерывной,
- конечной.
Кроме того, она должна иметь непрерывную и конечную производную.
Перечисленные требования называют стандартными условиями.
В теории дифференциальных уравнений доказывается, что уравнения вида (33.19), т.е. уравнения Шредингера для собственных значений, имеют решения не при любых значениях параметра (в уравнении (33.19) это энергия), а лишь принекоторых избранных. Эти значения называются собственными.
Решения уравнений, т. е. 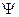 - функции соответствующие собственным значениям, называются собственными функциями.
- функции соответствующие собственным значениям, называются собственными функциями.
Совокупность собственных значений называется спектром физической величины. Спектры бывает дискретными или непрерывными, т. е. сплошными.
В случае дискретного спектра собственные функции можно пронумеровать.
Таким образом, квантование энергии вытекает из основных положений квантовой механики без дополнительных предположений.
 Рассмотрим частицу, находящуюся в бесконечно глубокой одномерной (частица может двигаться только вдоль х) потенциальной яме. В точках
Рассмотрим частицу, находящуюся в бесконечно глубокой одномерной (частица может двигаться только вдоль х) потенциальной яме. В точках 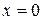 и
и 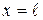 имеются непроницаемые для частицы стенки. Это означает, что потенциальная энергия частицы конечна в пределах ямы и бесконечна за ее пределами.
имеются непроницаемые для частицы стенки. Это означает, что потенциальная энергия частицы конечна в пределах ямы и бесконечна за ее пределами.
В одномерном случае квадрат оператора нала 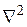 соответствует просто второй производной по избранной координате, поэтому уравнение Шредингера для стационарных состояний можно записать в следующем виде:
соответствует просто второй производной по избранной координате, поэтому уравнение Шредингера для стационарных состояний можно записать в следующем виде:
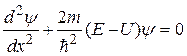 . (33.23)
. (33.23)
Поскольку за пределы ямы частица попасть не может, ее волновая функция должна обращаться в нуль. Стандартные условия требуют непрерывности волновой функции, следовательно, на границах ямы она тоже должна обращаться в нуль, а значит для 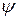 должны выполняться граничные условия
должны выполняться граничные условия
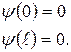 . (33.24)
. (33.24)
Поскольку потенциальная энергия определяется с точностью до произвольной постоянной, можно положить, что в пределах ямы она равна нулю 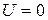 и представить уравнение Шредингера для частицы в пределах ямы в виде:
и представить уравнение Шредингера для частицы в пределах ямы в виде:
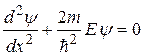 . (33.25)
. (33.25)
Обозначим положительную величину:
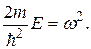 (33.26)
(33.26)
Тогда (33.25) примет знакомый вид:
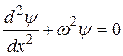 . (33.27)
. (33.27)
Общее решение уравнения (33.27) имеет вид:
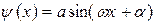 . (33.28)
. (33.28)
Решение уравнения (33.27) должно удовлетворять граничным условиям (33.24). Из условия 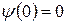 следует:
следует:
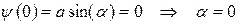 . (33.29)
. (33.29)
Из условия 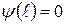 получаем:
получаем:
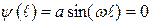 . (33.30)
. (33.30)
(33.30) выполняется, если
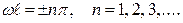 . (33.31)
. (33.31)
Вспомним обозначение (33.26) : 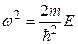 и подставим его (33.30)
и подставим его (33.30)
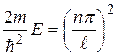 . (33.32)
. (33.32)
Выразив энергию из (33.32), получим:
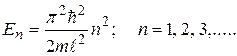 . , (33.33)
. , (33.33)
 И приходим к выводу о том, что спектр энергии у частицы в бесконечно глубокой яме оказывается дискретным. Графически его можно представить в виде показанном на рисунке 33.3.
И приходим к выводу о том, что спектр энергии у частицы в бесконечно глубокой яме оказывается дискретным. Графически его можно представить в виде показанном на рисунке 33.3.
Представляет интерес оценить расстояние между соседними энергетическими уровнями:
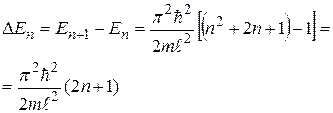 . (33.34)
. (33.34)
Рассматриваемая нами бесконечно глубокая потенциальная яма может служить моделью некоторых реальных объектов. Например, рассмотрим молекулы газа в сосуде с размерами 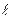
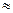
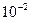 м. Массу молекул оценим величиной порядка
м. Массу молекул оценим величиной порядка 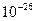 кг. Тогда расстояние между соседними энергетическими уровнями
кг. Тогда расстояние между соседними энергетическими уровнями
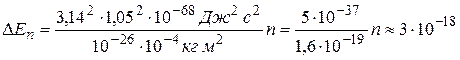 эВ.
эВ.
Оказывается, что энергетические уровни молекул расположены очень густо. Для сравнения вспомним, что тепловая энергия молекул имеет величину порядка 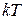 , и при комнатных температурах составляет около
, и при комнатных температурах составляет около  эВ. В таких условиях факт дискретности энергетических уровней молекул ни коим образом не будет сказываться на их движении.
эВ. В таких условиях факт дискретности энергетических уровней молекул ни коим образом не будет сказываться на их движении.
Другой важный пример представляет собой электронный газ в металле. На поверхности металла потенциальная энергия изменяется скачком и электроны при нормальных условиях в заметных количествах покинуть металл не могут. Расчет показывает, что энергетические уровни электронов тоже очень густо расположены – на расстояниях по энергиям порядка 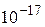 эВ.
эВ.
Электрон, связанный с атомом тоже можно рассматривать находящимся в потенциальной яме. Однако яма в этом случае имеет размеры порядка атомных – 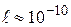 м и энергетическое расстояние между соседними уровнями – весьма существенным:
м и энергетическое расстояние между соседними уровнями – весьма существенным: 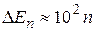 эВ.
эВ.
Подставив в общее решение (33.28) 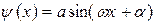 значение
значение  (33.31) найдём собственные функции частицы:
(33.31) найдём собственные функции частицы:
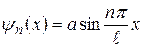 . (33.35)
. (33.35)
Для нахождения константы а воспользуемся условием нормировки, которые в данном случае можно записать в виде:
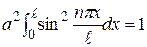 . (33.36)
. (33.36)
Поскольку подынтегральная функция обращается в нуль на концах промежутка интегрирования, то значение этого интеграла можно получить, умножив среднее, на длину промежутка:
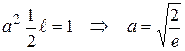 . (33.37)
. (33.37)
В окончательном виде собственные функции частицы представим следующим образом:
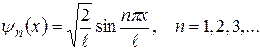 . (33.38)
. (33.38)
Графически примерный вид волновых функций частицы в бесконечно глубокой потенциальной яме показан на рисунке 33.4. На том же рисунке показаны графики квадрата волновой функции. Очевидно, что поведение квантовой (для которой существенны квантовые эффекты) частицы существенно отличается от классической.
 Если вероятность обнаружения обычной частицы одинакова в любой точке в пределах ямы, то квантовая частица в основном состоянии, с минимальной энергией (
Если вероятность обнаружения обычной частицы одинакова в любой точке в пределах ямы, то квантовая частица в основном состоянии, с минимальной энергией ( 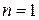 ), вблизи стен ямы вообще практически не появляется. В то же время вероятность найти ее в центре ямы максимальна.
), вблизи стен ямы вообще практически не появляется. В то же время вероятность найти ее в центре ямы максимальна.
В состоянии с 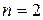 частица не может быть обнаружена точно в центре ямы, но в обеих ее половинах может быть обнаружена с одинаковой вероятностью.
частица не может быть обнаружена точно в центре ямы, но в обеих ее половинах может быть обнаружена с одинаковой вероятностью.
Дата добавления: 2016-02-11; просмотров: 3606;
