Статистической функцией распределения случайной величины Х называется частота события Х < х в данном статистическом материале.
F*(x)=P*(X<x).
Для того чтобы найти значение статистической функции распределения при данном х, достаточно подсчитать число опытов, в которых величина Х приняла значение, меньшее чем х, и разделить на общее число n произведенных опытов.
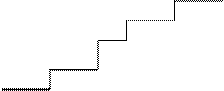
График статистической функции распределения величины представлен на рис.

 1 F(β)
1 F(β)
 | |||
 |
Статистическая функция распределения любой случайной величины—прерывной или непрерывной—представляет собой прерывную ступенчатую функцию, скачки которой соответствуют наблюденным значениям случайной величины и по величине равны частотам этих значений. Если каждое отдельное значение случайной величины Х было наблюдено только один раз, скачок статистической функции распределения в каждом наблюlенном значении равен 1/n, где n число наблюдений.
При увеличении числа опытов n, согласно теореме Бернулли, при любом х частота события Х < х приближается (сходится по вероятности) к вероятности этого события. Следовательно, при увеличении n статистическая функция распределения F* (х) приближается (сходится по вероятности) к подлинной функции распределения F(x) случайной величины X.
Если Х—непрерывная случайная величина, то при увеличении числа наблюдений n число скачков функции (х) увеличивается, самые скачки уменьшаются и график функции F*(x) неограниченно приближается к плавной кривой F(x)—функции распределения величины X.
В принципе построение статистической функции распределения уже решает задачу описания экспериментального материала. Однако при большом числе опытов n построение F* (х) описанным выше способом весьма трудоемко. Кроме того, часто бывает удобно — в смысле наглядности — пользоваться другими характеристиками статистических распределений, аналогичными не функции распределения F (х), а плотности f(x). С такими способами описания статистических данных мы познакомимся в следующем параграфе.
Статистический ряд. Гистограмма
При большом числе наблюдений (порядка сотен) простая статистическая совокупность перестает быть удобной формой записи статистического материала — она становится слишком громоздкой и мало наглядной. Для придания ему большей компактности и наглядности статистический материал должен быть подвергнут дополнительной обработке — строится так называемый «статистический ряд».
Предположим, что в нашем распоряжении результаты наблюдений над непрерывной случайной величиной X, оформленные в виде простой статистической совокупности. Разделим весь диапазон наблюденных значений Х на интервалы или «разряды» и подсчитаем количество значений mi приходящееся на каждый i-й разряд. Это число разделим на общее число наблюдений n и найдем частоту, соответствующую данному разряду:
Рi =mi / n
Сумма частот всех разрядов, очевидно, должна быть равна единице,
Построим таблицу, в которой приведены разряды в порядке их расположения вдоль оси абсцисс и соответствующие частоты. Эта таблица называется статистическим рядом:
| Ii | х1, X2 | x2; X3 | ... | Xi,Xi+1 | • . • | xk,xk+1 |
| Pi | P1 | P2 | ... | Pi | . . . | рk |
Здесь /,—обозначение i-го разряда; хi, Xi+1—его границы; рi'— соответствующая частота; k — число разрядов.
Пример 1. Результаты измерений () сведены в статистический ряд:
| Ii | -4; -3 | -3; —2 | -2; -1 | -1; 0 | 0; 1 | 1:2 | 2; 3 | 3; 4 |
| mi | ||||||||
| Pi* | 0,012 | 0,050 | 0,144 | 0,266 | 0,240 | 0,176 | 0,092 | 0,020 |
Здесь Ii обозначены интервалы значений ошибки наводки; mi—число наблюдений в данном интервале, рi = mi/n - соответствующие частоты.
При группировке наблюденных значений случайной величины по разрядам возникает вопрос о том, к какому разряду отнести значение, находящееся в точности на границе двух разрядов. В этих случаях можно рекомендовать (чисто условно) считать данное значение принадлежащим в равной мере к обоим разрядам и прибавлять к числам m-i того и другого, разряда по 1/2.
Число разрядов, на которые следует группировать статистический материал, не должно быть слишком большим (тогда ряд распределения становится невыразительным, и частоты в нем обнаруживают незакономерные колебания); с другой стороны, оно не должно быть слишком малым (при малом числе разрядов свойства распределения описываются статистическим рядом слишком грубо). Практика показывает, что в большинстве случаев рационально выбирать число разрядов порядка 10—20. Чем богаче и однороднее статистический материал, тем большее число разрядов можно выбирать при составлении статистического ряда. Длины разрядов могут быть как одинаковыми, так и различными. Проще, разумеется, брать их одинаковыми. Однако при оформлении данных о случайных величинах, распределенных крайне неравномерно, иногда бывает удобно выбирать в области наибольшей плотности распределения разряды более узкие. чем в области малой плотности.
Статистический ряд часто оформляется графически в виде так называемой гистограммы.. Гистограмма строится следующим образом. По оси абсцисс откладываются разряды, и на каждом из разрядов как их основании строится прямоугольник, площадь которого равна частоте данного разряда. Для построения гистограммы нужно частоту каждого разряда разделить на его длину и полученное число взять в качестве высоты прямоугольника. В случае равных по длине разрядов высоты прямоугольников пропорциональны соответствующим частотам. Из способа построения гистограммы следует, что полная площадь ее равна единице.
 |
 0 1 2 3 4 5 X
0 1 2 3 4 5 X
Очевидно, при увеличении числа опытов можно выбирать все более и более мелкие разряды; при этом гистограмма будет все более приближаться к некоторой кривой, ограничивающей площадь, равную единице. Нетрудно убедиться, что эта кривая представляет собой график плотности распределения величины X.
Пользуясь данными статистического ряда, можно приближенно построить и статистическую функцию распределения величины X. Построение точной статистической функции распределения с несколькими сотнями скачков во всех наблюденных значениях Х слишком трудоемко и себя не оправдывает.
Дата добавления: 2016-02-20; просмотров: 2194;
