Дискретные системы управления
6.1. Общая характеристика дискретных систем
Дискретные системы отличаются от непрерывных систем тем, что сигналы в одной или нескольких точках таких систем представляют собой последовательность импульсов или цифровой код. В литературе к таким системам применяются еще термины: «импульсные системы», «цифровые системы» [1].
Дискретные сигналы (импульсы, цифровой код) получаются из непрерывных (аналоговых) сигналов квантованием по уровню (релейные системы), по времени (импульсные системы) или одновременно и по уровню, и по времени (цифровые системы) [1].
Системы, в структуре которых используются цифровые устройства, контроллеры, микропроцессоры, вычислительные комплексы, являются дискретными. Примерами дискретных систем управления являются системы, использующие в контуре управления цифровые регуляторы. Непрерывный сигнал, поступающий на вход такого регулятора, преобразуется в последовательность импульсов. Эта последовательность в соответствии с законом регулирования преобразуется в другую последовательность, которая превращается в непрерывный сигнал регулятора.
Непрерывная система с цифровым регулятором:
|
|
|
 |  |  |  |
где: АЦП – аналогово-цифровой преобразователь;
ЦАП – цифро-аналоговый преобразователь.
Цифровая система управления:
|
 |  |  |

Примеры дискретных систем: система управления движением робота, система автономного слежения за целью, автопилот, цифровой контроллер турбины и генератора, радарные системы и др.
Дискретные системы обладают следующими преимуществами по сравнению с непрерывными системами:
· повышенной чувствительностью;
· меньшими габаритными размерами и массой;
· удобством программирования.
6.2. Математические модели линейных дискретных систем
Модели состояния дискретной системы
Математические модели дискретных систем описывают поведение этих систем только в квантованные моменты времени tk, k = 0, 1, 2,…. .
Дискретным представлением непрерывных сигналов u(t), y(t) и координат состояния x(t) являются последовательности:
{u(tk )},{y(tk )},{x(tk )}.
Математические модели дискретных систем устанавливают взаимосвязь между этими последовательностями.
Дискретные системы содержат в своей структуре цифровую (дискретную) и непрерывную (аналоговую) части. Для согласования этих частей в системе используются: АЦП – аналогово-цифровой преобразователь и ЦАП – цифро-аналоговый преобразователь.
Преобразователь «аналог - цифра» - идеальный импульсный элемент, ставящий в соответствие непрерывной функции f(t) при t ≥ t0 последовательность: {f(tk ), k = 0, 1, 2,….} = f*(t).
Преобразователь «цифра - аналог» осуществляет преобразование последовательности: {f(tk ), k = 0, 1, 2,….} в некоторую непрерывную функцию f^(t), которая является аппроксимацией исходной:
f^(t) ≈ f(t) , t ≥ t0
Наиболее часто используют кусочно-постоянную аппроксимацию (такой преобразователь называется экстраполятором или фиксатором нулевого порядка).
Построение дискретного представления непрерывной системы называется дискретизацией (квантованием).
Пусть линейная непрерывная стационарная система n-го порядка представлена своей внутренней моделью [2]:
X’(t) = A * X(t) + B * U(t)
Y(t) = C * X(t)
Предположим, что все переменные квантуются синхронно с постоянным шагом: ˅k, tk+1 – tk = h
Поэтому: tk = k h, k = 0, 1, 2,….
При этом обозначения эквивалентны:
x(tk) = x(kh) = x(k) = xk
В общем случае на текущий момент времени t для непрерывной системы (A,B,C), которая движется из начального состояния x(tk), можно записать в форме Коши:
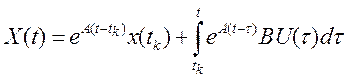
Так как преобразователь «цифра - аналог» является фиксатором нулевого порядка, то на любом интервале [tk,tk+1) управление сохраняет свое значение U(k), поэтому на интервале [0,t1) состояние х(1) равно:
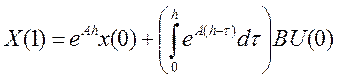
На интервале [t1, t2):
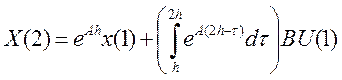
На интервале [tk, tk+1):
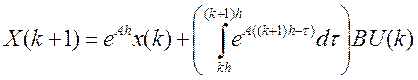
Все интегралы, стоящие в скобках равны. Сделав две замены переменных: z = τ – kh, h – z = θ, получим:
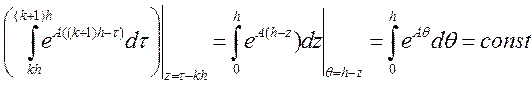
Обозначив: 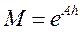
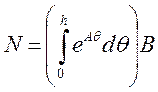
получим уравнения состояния системы в квантованные моменты времени (дискретную внутреннюю модель системы):
x(k+1) = M * x(k) + N * U(k)
y(k) = C * x(k)
k = 0, 1, 2,…
Эта модель при известной входной последовательности:
{U(k), k = 0, 1, 2,…} позволяет, выполнив итерации, найти решение:
x(1) = M*x(0) + N*U(0) ;
x(2) = M*x(1) + N*U(1) = M2*x(0) + M*N*U(0) + N*U(1);
x(3) = M*x(2) + N*U(2) = M3*x(0) + M2*N*U(0) + M*N*U(1)+ N*U(2);
………………………………………………………………………………………..
x(k) = Mk*x(0) + Mk-1*N*U(0) + Mk-2*N*U(1)+ …. + N*U(k-1)
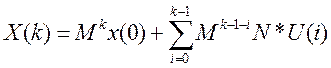
Матрицы дискретной модели системы M, N, C – матрицы состояния, входа и выхода.
Разностные уравнения
Пусть непрерывная модель представлена своей внешней моделью в виде дифференциального уравнения:
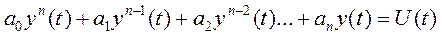
При малом шаге квантования дискретизация этой модели выполняется с необходимой точностью путем замены дифференциалов конечными разностями:
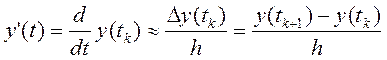
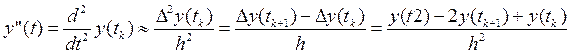
Дискретная внешняя модель системы имеет конечно-разностный вид:
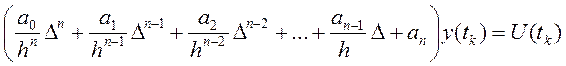
Этот вид после соответствующих алгебраических преобразований принимает рекуррентную форму:
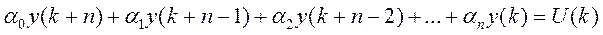 где αj, j=0, 1, 2,.. n – коэффициенты модели.
где αj, j=0, 1, 2,.. n – коэффициенты модели.
Рассмотрим разомкнутую систему, состоящую из импульсного элемента и непрерывной части. Передаточную функцию непрерывной части обозначим через W0(s). Импульсный элемент условно заменен последовательным соединением ключа и некоторого устройства с передаточной функцией Wф(s). Ключ периодически замыкается с периодом Т и выделяет из непрерывного сигнала U(t) его мгновенные значения U(kT).

|
|
 |  |  | |||||
 | |||||||
 T T y(kT)
T T y(kT)
 |  |
U(kT) = U(k), y(kT) = y(k) – решетчатые функции
Аналогом первой производной непрерывной функции для любой последовательности f(k) служит конечная разность первого порядка или первая разность:
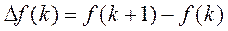
Она определяется в момент времени t = kT как разность между будущим значением последовательности при t = (k+1)T и текущим значением при t = kT.
Аналогом второй производной непрерывной функции для последовательности является разность второго порядка или вторая разность:
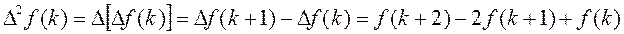
В общем случае для n-ой разности:
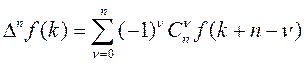 (5)где:
(5)где: 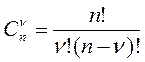
В качестве аналога дифференциального уравнения в математических моделях дискретных систем рассматривается уравнение в конечных разностях. Применительно к нашей системе оно имеет следующий вид:
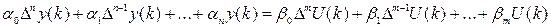 (6),
(6),
где: m ≤ n
При исследовании дискретных систем удобнее пользоваться таким уравнением, которое называется разностным (получается из (6) с учетом (5)):
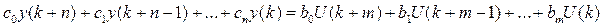 (7)
(7)
Уравнение (7) можно представить в виде:
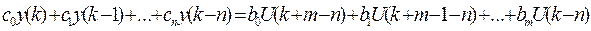 (8)
(8)
Общее решение неоднородного разностного уравнения (7) или (8) как и решение неоднородного дифференциального уравнения, представляется в виде суммы переходной и вынужденной составляющих.
Переходная составляющая определяется следующим образом:
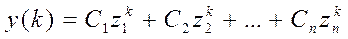 (9)
(9)
где: zυ (υ = 1, 2,…, n) – некратные корни характеристического уравнения, которое получается из (7):
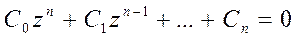
Из выражения (9) получается условие затухания свободного движения системы, описываемой разностным уравнением (7), т.е. условие устойчивости:
|zυ | < 1 (υ = 1, 2,…, n)
Решение разностного уравнения y(k) дает значение выходной величины лишь в дискретные моменты времени t = kT. Во многих случаях этого вполне достаточно для суждения о поведении системы.
Восстановление сигнала по дискретным выборкам
Во всех практических случаях невозможно точно восстановить непрерывный сигнал, если он квантован по времени; поэтому производят как можно более точную аппроксимацию исходной функции. Задача восстановления сигнала заключается в том, чтобы при имеющемся ряде чисел: f(0), f(T),…, f(kT) или последовательности импульсов с амплитудой равной f(kT) в момент времени t = kT (k = 0, 1, 2…) восстановить непрерывный сигнал f(t) при t ≥ 0 по информации, содержащейся в дискретных данных. Этот процесс рассматривается как процесс экстраполяции (непрерывные сигнал может быть восстановлен на основании информации, доступной только в предшествующие моменты выборки). Например, исходный сигнал f(t) между двумя моментами выборки kT и (k+1)T должен оцениваться на основании значении f(t) во все предшествующие моменты выборки: kT, (k-1)T, (k-2)T, …, 0 по значениям f(kT), f[(k-1)T],
f[(k-2)T],…, f(0).
Метод получения требуемой аппроксимации основан на разложении f(t) в ряд на интервале между моментами выборки kT и (k+1)T:
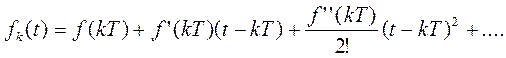 (10)
(10)
где:
fk(t) = f(t) для kT ≤ t < (k+1)T
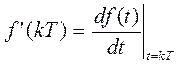
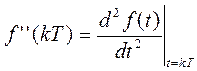
Оценка первой производной f(t) в момент t = kT равна:
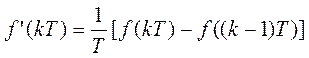
Аналогично для второй производной f’’(kT) запишем:
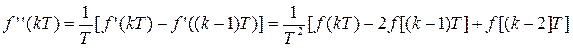
где: f’[(k-1)T] = 1/T [ f[(k-1)T] – f[(k-2)T] ]
Из полученных выражений для f’(kT) и f’’(kT) видно, что чем выше порядок производной функции, которую нужно аппроксимировать, тем требуется большее число предшествующих выборок. Так для аппроксимации значения fn(kT) число предшествующих выборок равно n+1.
На практике используется только первое слагаемое выражения (10), так как экстраполяция (восстановление) высокого порядка затратна при реализации устройств и требует сложных схемотехнических решений.
Устройство, в котором реализовано только слагаемое f(kT) из выражения (10) для временного интервала kT ≤ t < (k+1)T называют экстраполятором (фиксатором: оно фиксирует значение предыдущей выборки в течение периода квантования до следующей выборки) нулевого порядка (используемый полином имеет нулевой порядок).
Устройство, использующее два слагаемых выражения (10) называется фиксатором 1-го порядка и т.д.
Для фиксатора нулевого порядка:
fk(t) = f(kT)
Переходная функция фиксатора нулевого порядка равна:
h(t) = 1(t) – 1(t-T), где Т – период квантования.
Передаточная функция фиксатора нулевого порядка определяется:
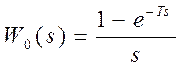
Выходной сигнал фиксатора нулевого порядка является ступенчатой аппроксимацией непрерывного сигнала, при этом с увеличением частоты (уменьшением периода) квантования повышается точность этой аппроксимации.
Использование Z-преобразования
Z-преобразование является одним из математических методов, разработанных для анализа и проектирования дискретных систем. Оно играет ту же роль, что и преобразование Лапласа для непрерывных систем.
Преобразование Лапласа квантованного сигнала определяется выражением:
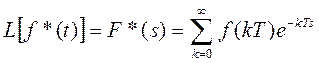
Функция F*(s) является иррациональной, поскольку содержит множитель e-Ts. Из-за этого множителя возникают трудности в вычислении обратного преобразования Лапласа. Поэтому для преобразования функции F*(s) в рациональную функцию комплексную переменную s заменяют на комплексную переменную z: z = eTs. Тогда:
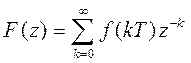
Для любой функции f(t), имеющей преобразование Лапласа, существует также Z-преобразование.
Преобразование Лапласа и его обратное преобразование являются однозначными, для Z-преобразования обратное Z-преобразование не является однозначным.
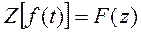
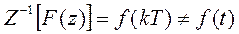
Корректным результатом обратного Z-преобразования функции F(z) является функция f(kT), которая равна функции f(t) только в моменты квантования t = kT.
Основные свойства Z-преобразования (без доказательств)
1. Суммирование и вычитание:
Если функции f1(t) и f2(t) имеют Z-преобразования:
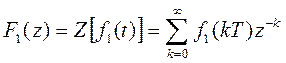
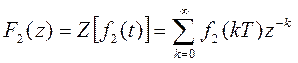
То выполняется следующее равенство:
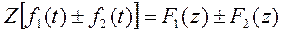
2. Умножение на константу:
Если функция F(z) есть Z[f(t)], то:
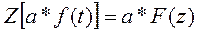
3. Сдвиг во временной области:
Если функция f(t) имеет Z-преобразование, то:
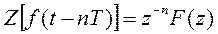
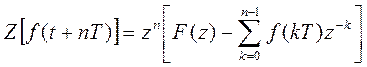
Где: n – положительное целое число.
4. Умножение оригинала на экспоненту:
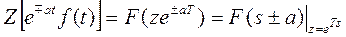
5. Теорема о начальном и конечном значении:
Если f(t) имеет Z-преобразование F(z) и существует предел: lim F(z) при z→∞, то:
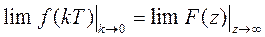
Если функция (1-z-1)F(z) не имеет полюсов на окружности единичного радиуса |z| =1или вне ее на Z-плоскости:
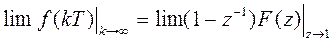
Ограничения метода Z-преобразования:
· время квантования должно быть намного меньше определяющей постоянной времени системы;
· Z-преобразование выходного сигнала линейной системы определяет значения функции f(t) только в моменты квантования и не содержит информацию о значениях функции f(t) между моментами квантования;
· При анализе линейной системы методами Z-преобразования передаточная функция непрерывной системы W(s) должна иметь полюсов, по крайне мере, на один больше, чем нулей (должна быть строго правильной функцией) для отсутствия разрыва в импульсной переходной характеристики при t = 0.
Передаточные функции дискретной системы
Дискретным аналогом оператора дифференцирования непрерывных функций d/dt является оператор сдвига вперед R, определяющийся соотношением:
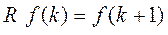
Инверсией оператора сдвига вперед является оператор сдвига назад R-1:
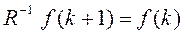
Оператор R-1 – дискретный аналог оператора интегрирования.
Пусть модель дискретной системы с одним входом и одним выходом представлена разностным уравнением общего вида:
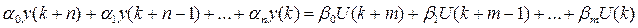 Запишем это уравнение в операторной форме:
Запишем это уравнение в операторной форме:
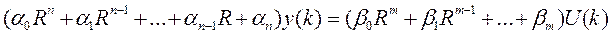
Обозначим:
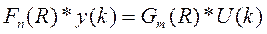
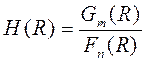
Теперь модель дискретной системы принимает следующий вид:
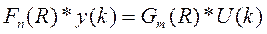 или
или 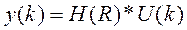
где: H(R) – дискретная операторная передаточная функция системы.
Пусть дискретная система имеет векторный вход и векторный выход, и описывается матричной моделью состояний [2]:
x(k+1) = M * x(k) + N * U(k)
y(k) = C * x(k)
k = 0, 1, 2,…
Применим к этой модели оператор сдвига вперед, получим:
x(k) = (R*E – M)-1 * N * U(k)
y(k) = C * (R*E – M)-1 * N * U(k)
H(R) = C *(R*E – M)-1 * N – матричная дискретная операторная передаточная функция системы.
Применим Z-преобразование к матричной модели состояний, получим:
Z[x(k+1)] = Z[ M * x(k) + N * U(k)]
Z[y(k)] = Z[C * x(k)]
z (X(z) – X(0)) = M * X(z) + N * U(z)
Y(z) = C * X(z)
где: X(z) = Z[x(k)]; Y(z) = Z[y(k)]; U(z) = Z[U(k)]
Отсюда получим:
X(z) = (z*E – M)-1 * [z *x(0) + N * U(z)]
Y(z) = C *(z*E – M)-1 * z *x(0) + C *(z*E – M)-1 * N * U(z)]
По аналогии с непрерывными системами введем понятие передаточной функции. Пусть дискретная система в начальный момент была в покое: x(0)=0; тогда:
Y(z) = C *(z*E – M)-1 * N * U(z)]
где: H(z) = C *(z*E – M)-1 * N – передаточная функция дискретной системы.
Связь между функциями H(R) и H(z): замена оператора R на переменную z, если в начальный момент система была в покое.
|
X(s) Y(s)
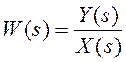
|

 x(t) x*(t) y(t)
x(t) x*(t) y(t)
 |  | ||||
 | |||||
X(s) X*(s) Y(s)

 T T y*(t)
T T y*(t)
 |  |
Y*(s)
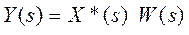
Где: X*(s)- преобразование Лапласа дискретного сигнала
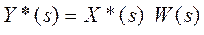
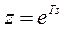
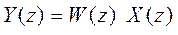 (11)
(11)
Если выходной сигнал системы непрерывный, то выражение (11) определяет выходной сигнал Y(z) только в моменты квантования.
W(z) – дискретная передаточная функция линейной системы. Она связывает Z-преобразование входного сигнала X(z) с Z-преобразованием выходного сигнала Y(z) подобно тому, как передаточная функция непрерывной системы W(s) связывает изображения Y(s) и X(s). В выражении (11) Z-преобразование определяет непрерывный сигнал y(t) только в дискретные моменты времени t = kT. В большинстве случаев потеря информации между моментами квантования не имеет значения. В других случаях, если в сигнале y(t) между моментами квантования содержатся колебания большой амплитуды, метод Z-преобразования дает неправильные результаты.
Дискретная система с последовательным соединением звеньев:
|
|

 x(t) x*(t) y1(t) y1*(t) y(t)
x(t) x*(t) y1(t) y1*(t) y(t)
 |  |  |  | ||||||
 | |||||||||
X(s) X*(s) Y1(s) T Y1*(s) Y(s)

 T y*(t)
T y*(t)

 T
T
Y*(s)
Y1(z) = W1(z)*X(z)
Y(z) = W2(z)*Y1(z) = W2(z)*W1(z)*X(z)
|
|
 x(t) x*(t) y1(t) y(t)
x(t) x*(t) y1(t) y(t)
 |  |  | |||||
 | |||||||
X(s) X*(s) Y1(s) Y(s)

 T y*(t)
T y*(t)

 T
T
Y*(s)
Z[W1(s)*W2(s)] = W1W2(z) = W2W1(z)
W1W2(z) ≠ W1(z)*W2(z)
Y(z) = W1W2(z) * X(z)
Взаимосвязь моделей системы
Пусть дискретная система содержит непрерывную часть, заданную передаточной функцией W(s) или матрицами состояния А, В, С.
Моделями дискретной системы являются передаточная функция W(z) или матрицы M, N, C. На вход непрерывной системы поступает единичный ступенчатый, однако чтобы это обеспечить необходимо на вход ЦАП подавать импульсную последовательность: U(kT) = 1, k = 0, 1, 2, ….
|
|
|
 |  |  |  |
Z-преобразование этой последовательности:
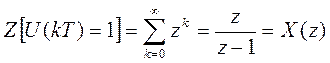
Преобразование Лапласа реакции непрерывной части системы, передаточная функция которой равна W(s), на единичное ступенчатое воздействие равно W(s) / s.
Выходной сигнал непрерывной системы проходит через АЦП и превращается в последовательность импульсов y(kT), k = 0, 1, 2, … , которая является реакцией Y(z) на входное единичное дискретное воздействие U(kT)=1, k =0, 1, 2, ……
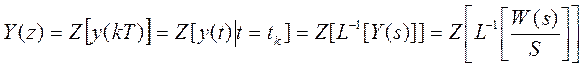 С другой стороны:
С другой стороны:
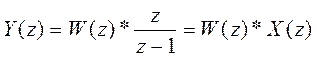
Значит, искомая передаточная функция дискретной системы определяется:
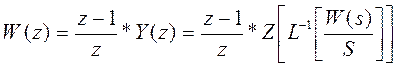
Ранее было установлено, что передаточная функция фиксатора нулевого порядка определяется как:
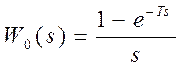
Z-преобразование W0(s) равно:
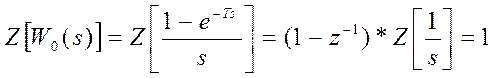
Это очевидно, так как фиксатор нулевого порядка в течение периода квантования удерживает постоянным дискретный сигнал, полученный в результате выборки. В том случае, если за фиксатором нулевого порядка следует непрерывная часть системы с передаточной функцией W(s), Z-преобразование выходного сигнала равно:
|
|
 x(t) x*(t) h(t) y(t)
x(t) x*(t) h(t) y(t)
 |  |  | |||||
 | |||||||
X(s) X*(s) H(s) Y(s)
T
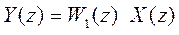
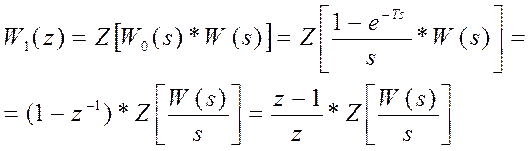
Дата добавления: 2016-02-20; просмотров: 5604;
