Основы метода эксергетического анализа
При анализе термодинамических систем необходимо учитывать на ряду с первым, второй закон термодинамики. Согласно второму закону термодинамики любой теплопроцесс характеризуется ростом энтропии системы. Следовательно, приращение энтропии системы может явиться
абсолютным критерием термодинамического совершенства анализируемого теплопроцесса. Сумма приращений энтропии по всем теплоиспользующим элементам будет определять подвод энергии от внешнего источника. Приращение энтропии в локальном теплоиспользующем элементе пропорционально перерасходу химической энергии топлива, например, в котле ТЭЦ или другой организованной формы подведенной энергии. Задачей термодинамического анализа является определение перерасхода топлива в каждом локальном теплопроцессе сложной термотехнологической системы, определение КПД этого локального теплопроцесса и его связь с КПД системы.
Метод термодинамического анализа, учитывающий при анализе технологических систем как первый, так и второй закон термодинамики называется эксергетическим.
Рассмотрим основные закономерности этого метода.
В процессе энергетического взаимодействия потоков друг с другом и с окружающей средой имеет место передача энергии материальных потоков с наинизшей температурой в системе окружающей среде. Действительно, согласно второму закону термодинамики эта энергия не может быть передана остальным рабочим телам с большей температурой, т. е. является бесполезной в данной системе и переходит в окружающую среду.
Рассмотрим (рис.1.5.) стационарную закрытую термически изолированную систему, отдающую энергию Q2 с температурой ТВ (низшая температура в системе) в окружающую среду (с температурой Тх), а также потребляющую извне энергию направленного движения Q1 и, в общем случае, энергию окружающей среды Q0 .
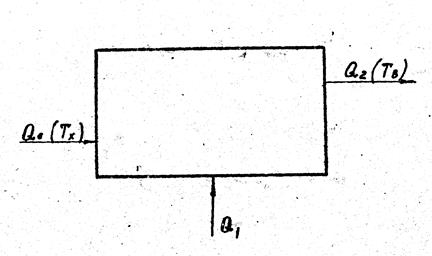
Рис. 1.5. Термически изолированная система
По первому закону термодинамики имеем
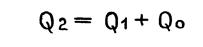
( 1. 4.)
Далее, по определению энтропии приращение энтропии системы равно
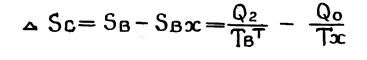
(1. 5.)
Sвх, Sвых - энтропии метериалъных потоков на входе и выходе из системы.
Из (1.4.) и с учетом (1.5.) находим
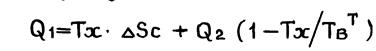 (1.6)
(1.6)
где ТвТ - среднетермодинамическая температура (при выборе в качестве точки отсчета тампературы Тх ); Тх - температура холодильника (окружающая среда);
Из полученного выражения видно, что при ТВТ = Тх , т. е при обратимом энергообмене с окружающей средой потребляемая извне энергия минимальна ( Qmin ) и компенсирует только потери от внутренней необратимости теплопроцессов в системе, т.е.
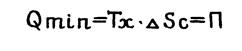
(1.7.)
Уравнение (1.7.) выражает закон Гюи – Стодолы.
Потери от внутренней необратимости тепловых процессов Пназываются эксергетическими потерями; величина
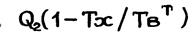 (1.8)
(1.8)
определяет потери эксергии от внешней необратимости .
Выведенные соотношения для общих затрат энергии в систему (1.4) и минимальных затрат (1.7) позволяют абсолютно оценить (через подвод энергии от внешнего источника) термодинамическое совершенство системы.
Термодинамический анализ технологических систем диктует необходимость относительной оценки степени термодинамического совершенства, т.е. термодинамического (эксергетического) к.п.д. Он может быть получен с использованием понятия эксергии теплового потока термодинамической системы.
Эксергия теплового потока Еq при температуре Т определяется количеством работы, которое может быть получено или должно быть затрачено в обратимом процессе переноса энтропии, характеризующей данный тепловой поток, на уровень температуры окружающей среды.
Эта термодинамическая функция характеризует не энергию теплового потока, а его максимально возможную работу, которую этот поток может совершить вне рассматриваемой системы. Следует подчеркнуть, что возможная работа теплового потока не является материальной величиной, поэтому для нее закон сохранения энергии не справедлив. Однако учет потерь от необратимости процессов (эксергетических потерь) позволяет составлять ее баланс и, следовательно, открывает возможность определения эксергетического КПД.
Математическое выражение для эксергии теплового потока в условиях изобарического процесса имеет вид
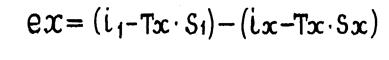
(1.9.)
Выразим приращение энтропии через среднетермодинамическую температуру потока, тогда
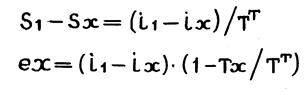
(1.10.)
(1.11.)
где i1, S1, ix, Sx, ex - удельная энтальпия, энтропия, эксергия потока при заданных параметрах и параметрах окружающей среды;
ТТ - среднетермодинамическая температура потока;
Тх – температура холодильника (окружающая среда).
Для анализа блоков термодинамической системы удобно пользоваться приращением эксергии, полученным при термическом взаимодействии материальных потоков.
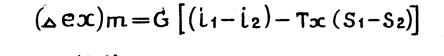
(1.12)
или с учетом (1.7.)
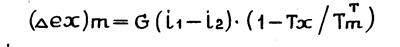
(1.13.)
где i1, S1, i2, S2, - энтальпия и энтропия подвода и отвода энергии от материальных потоков в анализируемом блоке системы;
G – массовый расход потока; ТmT - среднетермодинамическая температура потока (отвода) теплового потока в m – ом блоке термодинамической системы. Абсолютная оценка термодинамического совершенства выражается через эксергетические потери.
Эксергетические потери можно получить вычитанием всех входящих и выходящих в узел эксергий.
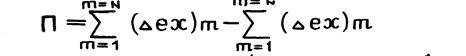
(1.14.)
Эксергетических потери – абсолютная мера необратимости процесса. Она также численно равна возрастанию энтропии участвующих в процессе взаимодействия материальных потоков через коэффициент пропорциональности Тх
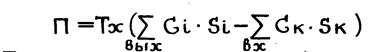
(1.15.)
где Тх – температура холодильника (окружающая среда) ;
Gк, Sк, Gi , Si , - расход и соответствующая ему энтропия i – го потока на выходе и входе в узел взаимодействия.
В качестве относительной характеристики термодинамического совершенства процесса выступает эксергетический КПД. Составленный на основе классических законов термодинамики (первого и второго), эксергетический к.п.д. характеризует степень необратимости процессов. Определение эксергетичеоких к.п.д. теплоиспользующих элементов системы позволяет выявить процессы, характеризующие большой необратимостью, наметить пути по уменьшению или ликвидации этой необратимости.
Эксергетический к.п.д. определяется как отношение воспринятой в теплопроцессе пригодной для дальнейшего технического использования энергии к подводимой, при годной для технического использования энергии т.е. как отношение приращения эксергий.
Эксергетический к.п.д. теплообменного аппарата можно выразить
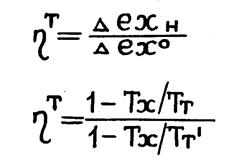
(1.16.)
(1.17.)
где Δехн , Δех0 - приращение эксергии нагреваемого и охлаждаемого потока при энергетическом взаимодействии;
Тт, ТтI – среднетермодинамическая температура нагреваемого и охлаждаемого потока.
Эксергетичеcкий к.п.д. сложной системы можно определить как отношение суммарного приращения эксергии всех нагреваемых потоков к суммарному приращению всех охлаждаемых потоков.
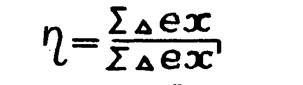
(1.18.)
Найдем связь η сложной тепловой схемы с η m cоставляющих ее локальных элементов. По определению имеем
Для m – го элемента сложной тепловой схемы
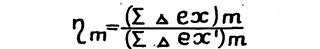
(1.19.)
Для сложной тепловой схемы
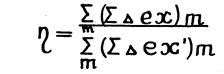
(1.20.)
Введем понятие доли затраченной эксергии в m – ом локальном элементе тепловой схемы к суммарным затратам эксергии во всей тепловой схеме – γ m
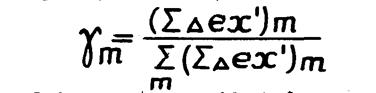
(1.21)
Тогда из (1.I6.) с учетом (1.17.) после несложных математических преобразований получим
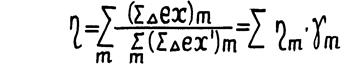
(1.22.)
Дата добавления: 2016-02-20; просмотров: 1436;
