Уравнение бегущей волны
Уравнение плоской и сферической волн
Уравнением волны называется выражение, которое даёт смещение колеблющейся частицы, относительно положения равновесия, как функцию её координат и времени.
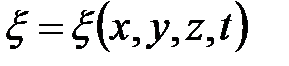 – уравнение волны
– уравнение волны
| фаза = const |
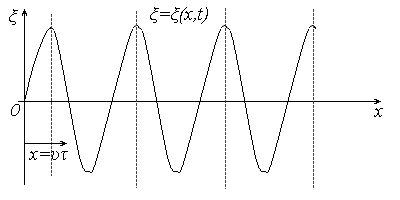
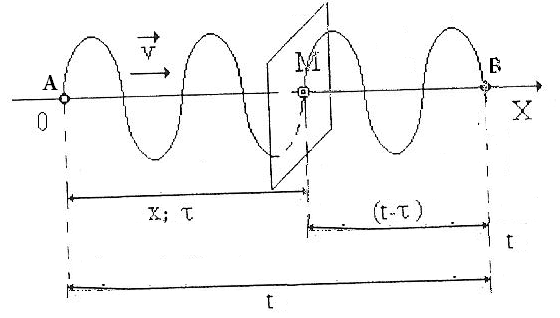
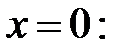
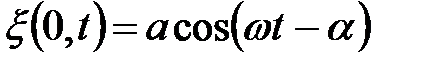
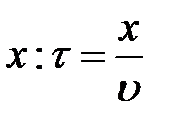
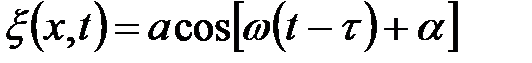 =
= 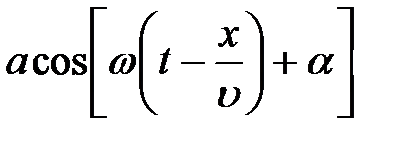
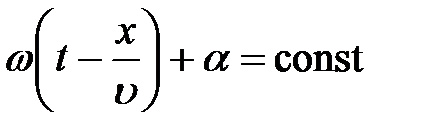
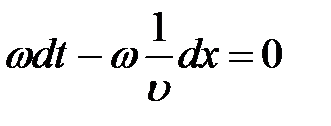
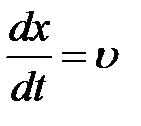 – фазовая скорость (скорость перемещения фазы)
– фазовая скорость (скорость перемещения фазы)
Вывод: скорость распространения волны есть скорость перемещения фазы волны, поэтому ее называют фазовой скоростью и обозначают: 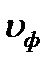 :
:
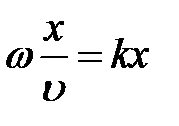 (
( 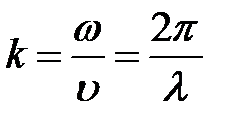 )
)
Т.к. 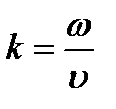 , отсюда
, отсюда 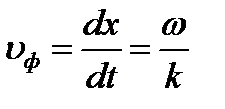
| Дисперсиейназывается зависимость фазовой скорости в среде от частоты распространение волн (дисперсия всегда связана с поглощением энергии средой) |
Физический смысл отношения 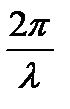 заключается в том, что оно показывает, сколько длин волн умещается в
заключается в том, что оно показывает, сколько длин волн умещается в 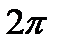 единицах длины. Отношение
единицах длины. Отношение 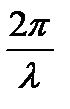 обозначается
обозначается 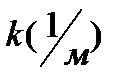 и называется волновым числом, т.е.
и называется волновым числом, т.е.



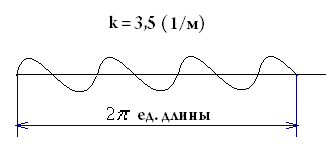
Например:
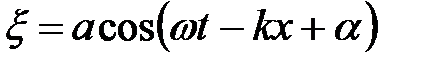 – волна движется вдоль оси Ох
– волна движется вдоль оси Ох
 – волна движется против оси Ох
– волна движется против оси Ох
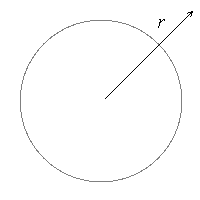
Для сферических колебаний:
 – без затухания
– без затухания
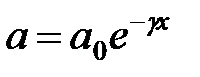 – закон затухания
– закон затухания
 – затухающая плоская волна
– затухающая плоская волна
Уравнение бегущей волны
Бегущими волнами называют волны, которые переносят в пространстве энергию.
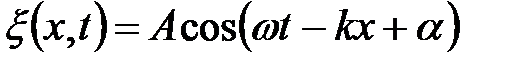
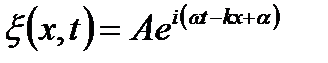
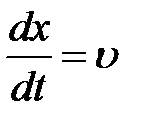 ;
; 
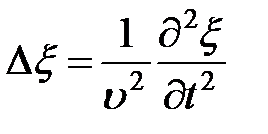 – волновое уравнение
– волновое уравнение
где 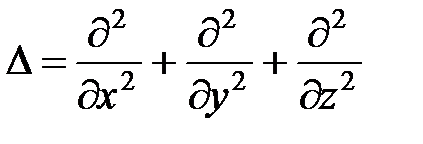 – оператор Лапласа
– оператор Лапласа
Для волны, распространяющейся вдоль оси Ох:
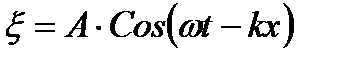
| - первый вид уравнения плоской бегущей волны | ||
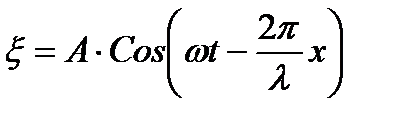
| - второй вид уравнения плоской бегущей волны | ||
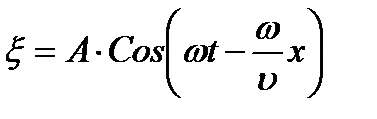
| - третий вид уравнения плоской бегущей волны | ||
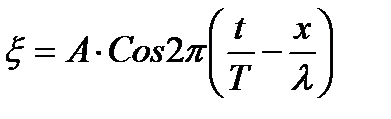
| - четвертый вид уравнения плоской бегущей волны | ||
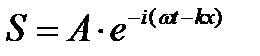
| - уравнения плоской бегущей волны в комплексном виде | ||
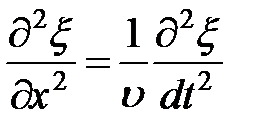
Итак:
Дата добавления: 2016-02-20; просмотров: 1163;
