Принцип суперпозиции. Групповая скорость

Рассмотрим простейшую группу волн, которая получается при наложении двух плоских волн с одинаковыми амплитудами и близкими частотами 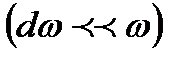и близкими волновыми числами :

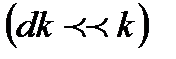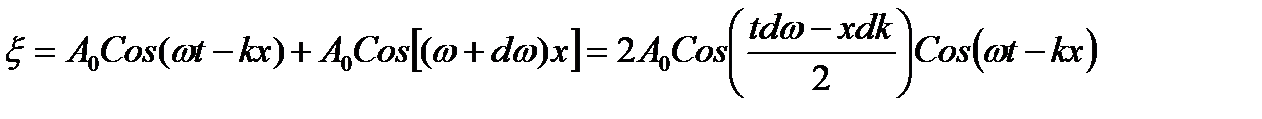Это волна отличается от гармонической тем, что ее амплитуда есть медленно изменяющаяся функция координаты от времени, т.е. является негармонической.

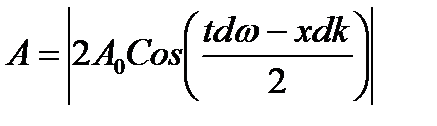
- амплитуда группы волн

Групповая скорость– скорость распространения группы волн,

Групповая скорость– скорость максимума огибающей группы волн или скорость движения центра волнового пакета.

Из условия 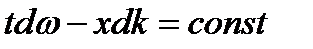получим: ,

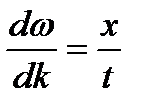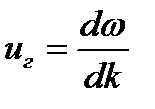
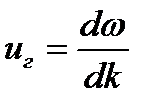
- групповая скорость

Связь групповой и фазовой скорости:

Групповая скорость определяется выражением:

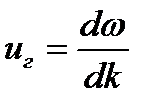
Определим отдельно выражения для 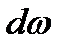и :

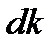1) - ?

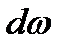Из выражения выразим угловую скорость: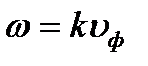

Продифференцируем это выражение по k: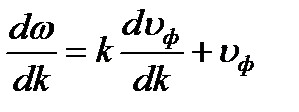

2) - ?

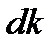Выражения продифференцируем по :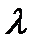

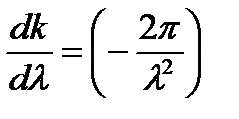или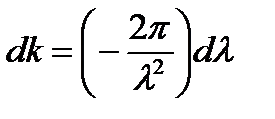

Подставим полученные выражения в выражение для групповой скорости, получим:

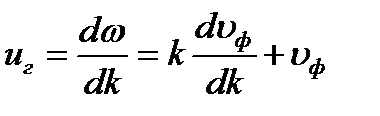
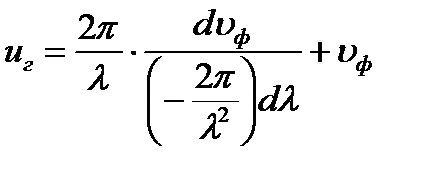
- связь фазовой и групповой скорости

Из этой формулы следует, что 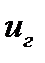может быть как больше, так и меньше фазовой в зависимости от знака 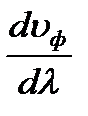. Если в среде не наблюдается дисперсия волн, то 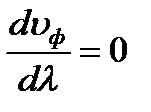, тогда фазовая и групповая скорости совпадают .

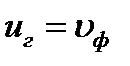Понятие групповой скорости очень значимо, т.к. именно она фигурирует при измерении дальности радиолокации, в управлении космическими объектами.

Но , а для 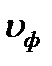ограничений нет.

Стоячие волны

Стоячие волны – это волны, образующиеся при наложении двух бегущих волн, распространяющихся с одинаковыми частотами, амплитудами и поляризацией (для поперечных), распространяются навстречу друг другу.

= =

=

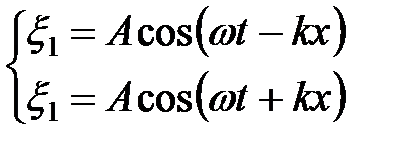
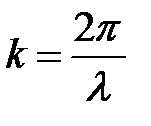
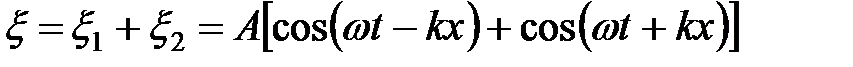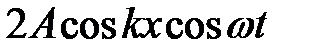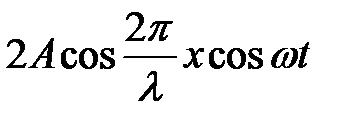
– амплитуда, меняющаяся по закону косинуса

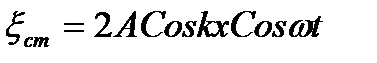
	- уравнение стоячей волны
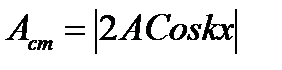
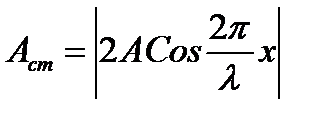
	- амплитуда стоячей волны

Пучности – точки, в которых амплитуда стоячей волны максимальна :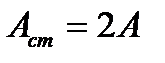

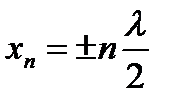
- координата пучности

Узлы стоячей волны – точки, в которых амплитуда стоячей волны равна нулю :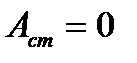

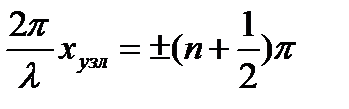
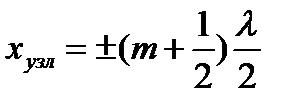
- координата узлов

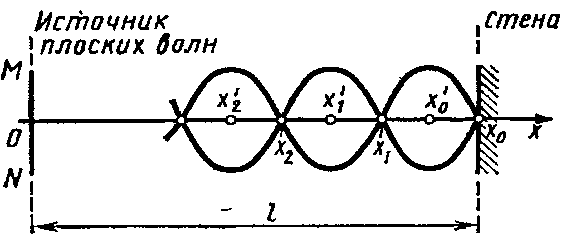
Границы максимальных смещений точек среды в зависимости от их координат изображены на рисунке. Здесь же отмечены коор­динаты х₀,, х₁, х₂ , ... узлов и координаты х'₀, х'₁, х'₂ ... пуч­ностей стоячей волны.